3.3 复数的几何意义课件15张PPT
文档属性
| 名称 | 3.3 复数的几何意义课件15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 108.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 21:46:51 | ||
图片预览




文档简介
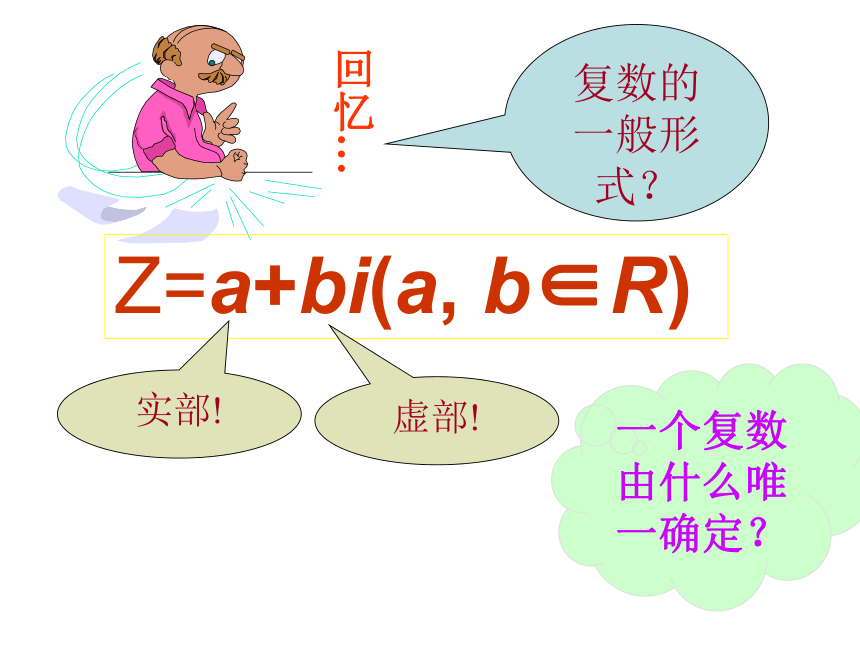
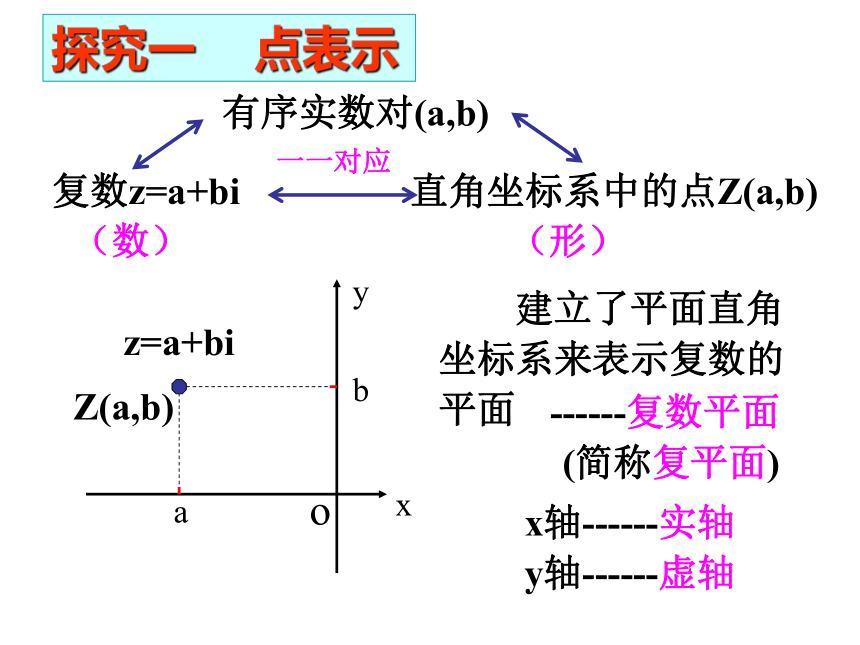
课件15张PPT。3.1.2《复数的几何意义》在几何上,我们用什么来表示实数?想一想?实数的几何意义类比实数的表示,可以用什么来表示复数?实数可以用数轴上的点来表示。实数 数轴上的点 (形)(数)一一对应 回忆…复数的一般形式?Z=a+bi(a, b∈R)实部!虚部!一个复数由什么唯一确定?复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi探究一 点表示(1)在复平面内,任意一点都对应于唯一
复数
(2)在复平面内,若两点关于实轴对称,则
这两点对应的复数共轭
(3)在复平面内,实轴上的点所对应的复
数都是实数;
(4)在复平面内,虚轴上的点所对应的复
数都是纯虚数。练一练:1.下列说法错误的是 2.已知复数z=(m2+m-6)+(m2+m-2)i在复平面
内所对应的点位于第二象限,求实数m的
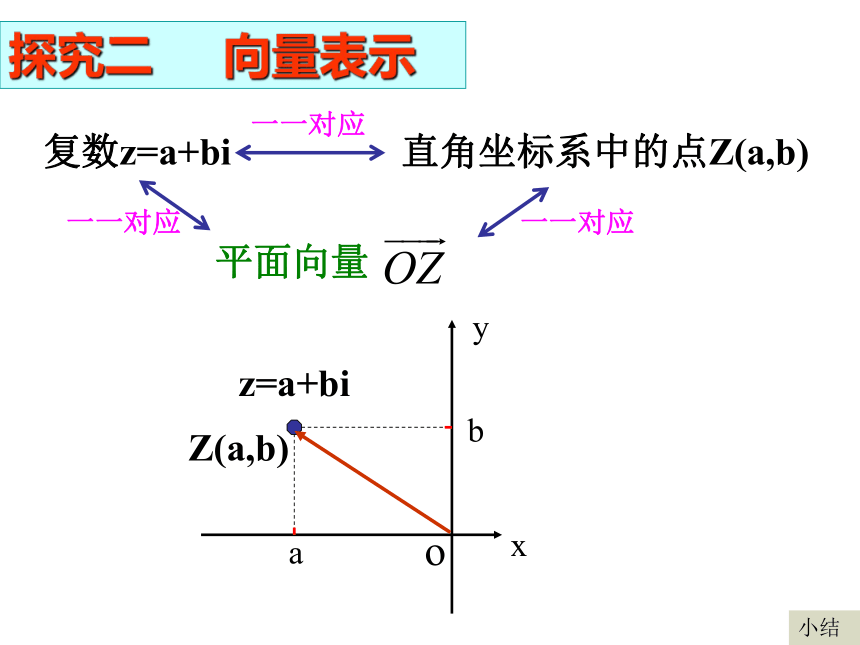
取值范围. 练一练:解:由题意可知复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应探究二 向量表示xyobaZ(a,b)z=a+bi小结例1在复平面内,分别用点和向量表示下列复数.4,2+i,-i,-1+3i,3-2i, 3+2ixOz=a+biy探究3 复数的模Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = | |小结例2 已知复数思考 任意两个复数都可以比较大小吗?试比较它们模的大小.(1)│Z│=2,(2)2<│Z│<3.xoyZ(a+c,b+d)符合向量加法的平行四边形法则.1.复数加法运算的几何意义?探究4 复数加、减法运算的几何意义xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离(1)|z+(1+2i)|例4.已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(-1, -2)的距离(2)|z+2i|点A到点(0, -2)的距离小结1.复数的几何意义.
2.复数加减法的几何意义.
3.数形结合的思想方法.
复数
(2)在复平面内,若两点关于实轴对称,则
这两点对应的复数共轭
(3)在复平面内,实轴上的点所对应的复
数都是实数;
(4)在复平面内,虚轴上的点所对应的复
数都是纯虚数。练一练:1.下列说法错误的是 2.已知复数z=(m2+m-6)+(m2+m-2)i在复平面
内所对应的点位于第二象限,求实数m的
取值范围. 练一练:解:由题意可知复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应探究二 向量表示xyobaZ(a,b)z=a+bi小结例1在复平面内,分别用点和向量表示下列复数.4,2+i,-i,-1+3i,3-2i, 3+2ixOz=a+biy探究3 复数的模Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = | |小结例2 已知复数思考 任意两个复数都可以比较大小吗?试比较它们模的大小.(1)│Z│=2,(2)2<│Z│<3.xoyZ(a+c,b+d)符合向量加法的平行四边形法则.1.复数加法运算的几何意义?探究4 复数加、减法运算的几何意义xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离(1)|z+(1+2i)|例4.已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(-1, -2)的距离(2)|z+2i|点A到点(0, -2)的距离小结1.复数的几何意义.
2.复数加减法的几何意义.
3.数形结合的思想方法.
