3.1.1 随机现象课件25张PPT
图片预览






文档简介
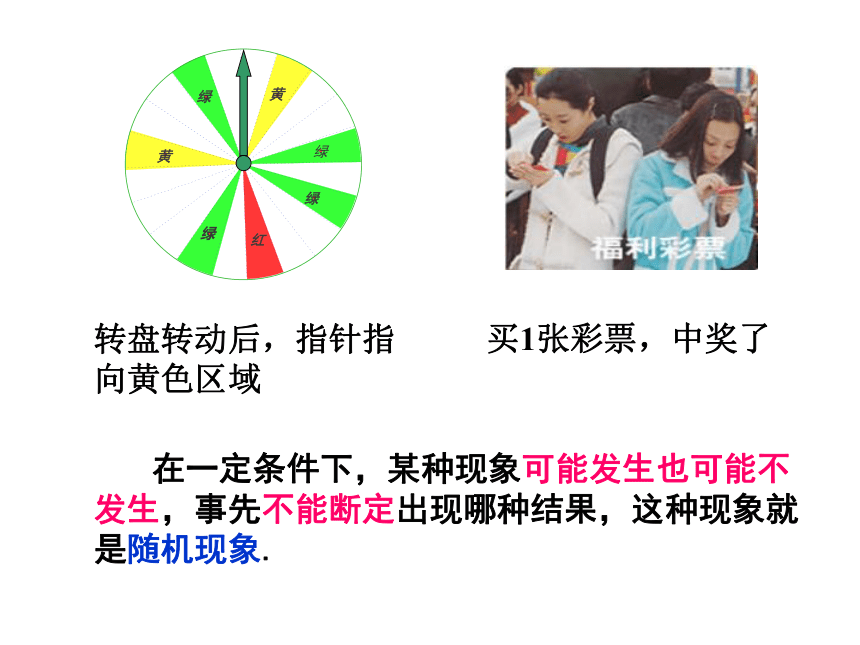
课件25张PPT。随机事件及其概率问题情境: 在一定条件下,事先就能断定发生或不发生某种结果,这种现象就是确定性现象.实心铁块丢入水中,铁块浮起 在一定条件下,某种现象可能发生也可能不发生,事先不能断定出现哪种结果,这种现象就是随机现象. 对于某个现象,如果能让其条件实现一次,就是进行了一次试验,试验的每一种可能的结果,都是一个事件. 如:掷一次骰子,篮球投一次篮等 .概念理解:
试验应当满足以下条件
(1)在不变的条件下是可能重复实现的;
(2)所有可能的试验结果都是预先明确的;
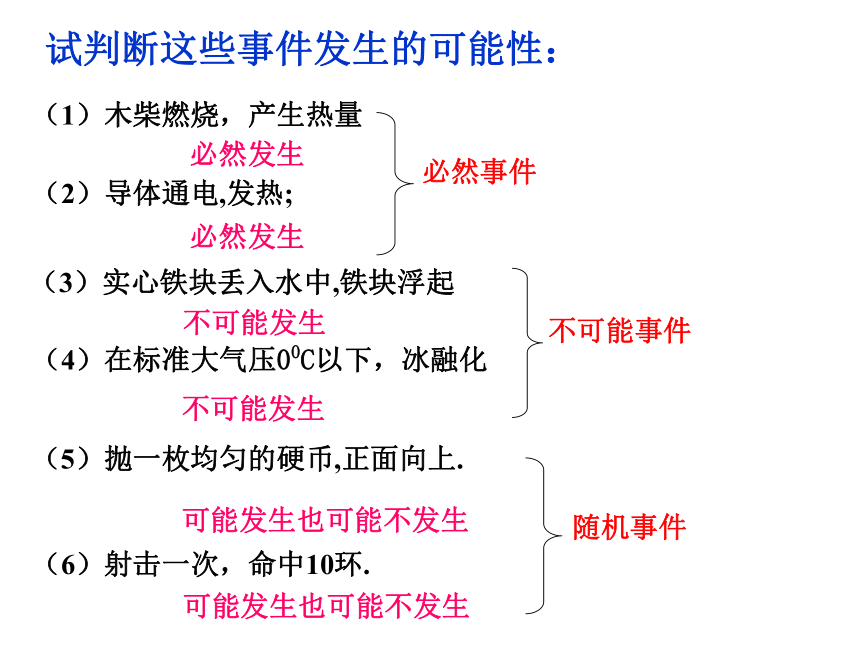
(3)各次试验的结果不一定相同,每次试验前不能预先知道是哪一个结果会发生。试验、事件的概念.(1)木柴燃烧,产生热量(2)导体通电,发热;(3)实心铁块丢入水中,铁块浮起(4)在标准大气压00C以下,冰融化(5)抛一枚均匀的硬币,正面向上.(6)射击一次,命中10环.试判断这些事件发生的可能性:不可能发生必然发生必然发生不可能发生可能发生也可能不发生可能发生也可能不发生随机事件:在一定条件下可能发生也可能不发生的事
件叫随机事件.必然事件:在一定条件下必然要发生的事件叫必然事件.不可能事件:在一定条件下不可能发生的事件叫不可
能事件.事件的表示:以后我们用A、B、C等大写字母表示随机事件,简称事件.数学理论:木柴燃烧,产生热量实心铁块丢入水中,铁块浮起买1张彩票,中奖数学运用:事件A:抛一颗骰子两次,向上的面的数字之和
大于12.
事件B:在地球上,抛一石块,下落;
事件C:打开电视机,CCTV5正在播放广告;
事件D:在下届亚洲杯上,中国足球队以2:0
战胜日本足球队
不可能事件必然事件随机事件随机事件例1.判断哪些事件是随机事件,哪些是必然事件,
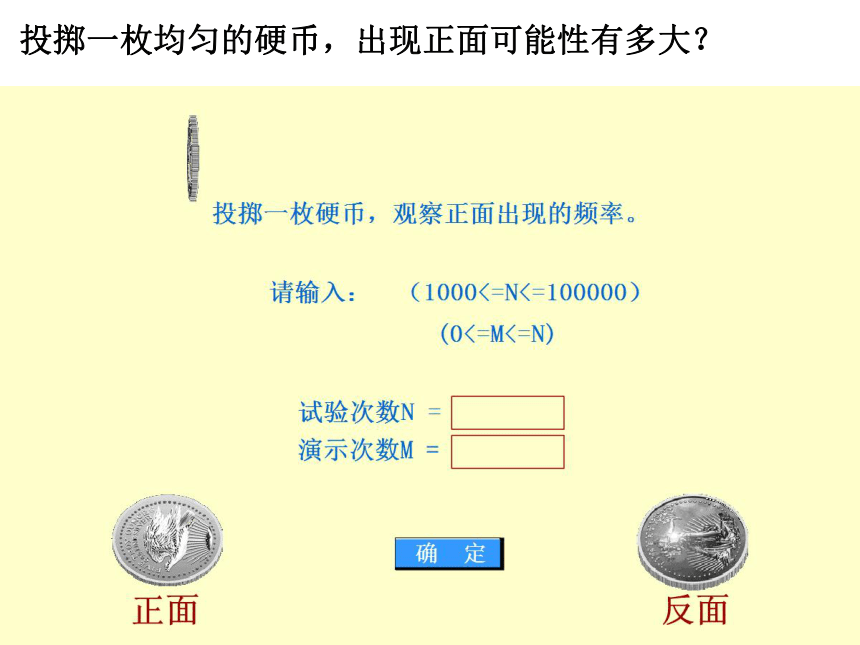
哪些是不可能事件?投掷一枚均匀的硬币,出现正面可能性有多大? 我们看到,当试验次数很多时,出现正面的频率接近于常数0.5,并在其附近摆动.1.频率的定义:相同条件下重复n次试验,观察某一事件A是否出现。若n次试验中事件A出现的次数为m,则称事件A出现的比例 为事件A出现的频率.2.一般的,对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性大小,并把这个常数称为随机事件A的概率,记作P(A)随机事件的概率定义理解:注意点:1.事件A的概率范围即随机事件发生的概率都满足:0概率越大,事件发生的可能性越大,概率越小,事件发生的可能性越小.2.随机事件A的概率的意义3.频率与概率的关系频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,并在其附近摆动.在实际问题中,若事件的概率未知,常用频率作为它的估计值.频率随着试验次数的变化而发生变化,在试验前不能确定,它不一定是常数;而概率是概率是一个确定的数,是客观存在的,与试验次数的多少无关.(1)联系:
(2)区别:例1. ①明天的下雨概率是60%是指( )
A.明天有60%的时间下雨
B.假如天气条件相同的天数是100天,那么恰好有60天要下雨
C.明天下雨的可能性是60%
D.明天有60%的地方要下雨 C例1. ②某医院治疗一种疾病的治愈率为10%, 那么前9个病人都没有治愈,第10个病人就一定能治愈,试从概率的角度解释这说法是否正确?答:不正确.
如果把治疗一个病人作为一次试验,治愈率为10%, 是指随着试验次数的增加,即治疗病人的增加,大约有10%的人能够治愈, 对于一次试验来说,其结果是随机的,因此前9个病人都没有治愈是可能的,对第10个病人来说,其结果仍然是随机的,即有可能治愈,也有可能没有治愈.治愈的可能性为10%.例2.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(1)试计算男婴各年出生频率(精确到0.001);
(2)该市男婴出生的概率约是多少?(1)1999年男婴出生的频率为:解题示范:同理可求得2000年、2001年和2002年男婴出生的频率分别为:0.521,0.512,0.512.(2) 各年男婴出生的频率在0.51~0.53之间,各频率都在0.52附近摆动,故该市男婴出生的概率约是0.52.1、指出下列事件是必然事件,不可能事件还是随机事件?(1)我国东南沿海某地明年将3次受到热带气旋的侵袭;
(2)若a为实数,则|a+1|+|a+2|=0;
(3)江苏地区每年1月份月平均气温低于7月份月平均气温;
(4)发射1枚炮弹,命中目标.练一练随机事件随机事件不可能事件必然事件BC4、某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能
投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 但可以说明的是:投10次篮,投中8次的可能性最大,即概率越大,事件发生的可能性越大.概率约是0.80.780.750.800.80 0.85 0.830.80做这种统计有意义吗? 密码破解:
我们随便找一个英语单词,比如cat,将每个字母向后移动一位,cat变成dbu,将每个字母向后移动两位,cat变成ecv,等等,这就是一种最原始、最简单的加密方法,19世纪以前曾在欧洲广泛使用.
但后来人们就利用了字母出现频率的多少,轻易破解了这种方法:利用字母e出现频率最高,大多数单词中都包含它的特征,观察加密电文中,出现次数最多的字母,假如是h,则就可以断定h就是e,原文的每个字母都向后移动了三位(e-f-g-h),因此只要将每个字母向前移动三位,即可看到明文. 做这种统计有意义吗? 男女出生率的研究:
一般人或许认为:生男生女的可能性是相等的,因而推测出男婴和女婴的出生数的比因当是1:1,可事实并非如此.
公元1814年,法国数学家拉普拉斯在他的新作<<概率的哲学探讨>>一书中,记载了一下有趣的统计.他根据伦敦,彼得堡,柏林和全法国的统计资料,得出了几乎完全一致的男婴和女婴出生数的比值是22:21,即在全体出生婴儿中,男婴占51.16%,女婴占48.84%.可奇怪的是,当他统计1745---1784整整四十年间巴黎男婴出生率时,却得到了另一个比是25:24,男婴占51.02%,与前者相差0.14%. 这千分之一点四的后面,隐藏了什么?拉普拉斯深入进行调查研究,终于发现:当时巴黎人”重女轻男”,又抛弃男婴的陋俗,以至于歪曲了出生率的真相!做这种统计有意义吗? 弗格森发现尚克斯关于π值计算中的错误;天气预报的改变;《红楼梦》作者的考证;…回顾小结:随机事件及其概率事件的含义事件的分类事件的表示频率与概率课后作业:课本 P91 习题3.1
No.1、2、3、5.
试验应当满足以下条件
(1)在不变的条件下是可能重复实现的;
(2)所有可能的试验结果都是预先明确的;
(3)各次试验的结果不一定相同,每次试验前不能预先知道是哪一个结果会发生。试验、事件的概念.(1)木柴燃烧,产生热量(2)导体通电,发热;(3)实心铁块丢入水中,铁块浮起(4)在标准大气压00C以下,冰融化(5)抛一枚均匀的硬币,正面向上.(6)射击一次,命中10环.试判断这些事件发生的可能性:不可能发生必然发生必然发生不可能发生可能发生也可能不发生可能发生也可能不发生随机事件:在一定条件下可能发生也可能不发生的事
件叫随机事件.必然事件:在一定条件下必然要发生的事件叫必然事件.不可能事件:在一定条件下不可能发生的事件叫不可
能事件.事件的表示:以后我们用A、B、C等大写字母表示随机事件,简称事件.数学理论:木柴燃烧,产生热量实心铁块丢入水中,铁块浮起买1张彩票,中奖数学运用:事件A:抛一颗骰子两次,向上的面的数字之和
大于12.
事件B:在地球上,抛一石块,下落;
事件C:打开电视机,CCTV5正在播放广告;
事件D:在下届亚洲杯上,中国足球队以2:0
战胜日本足球队
不可能事件必然事件随机事件随机事件例1.判断哪些事件是随机事件,哪些是必然事件,
哪些是不可能事件?投掷一枚均匀的硬币,出现正面可能性有多大? 我们看到,当试验次数很多时,出现正面的频率接近于常数0.5,并在其附近摆动.1.频率的定义:相同条件下重复n次试验,观察某一事件A是否出现。若n次试验中事件A出现的次数为m,则称事件A出现的比例 为事件A出现的频率.2.一般的,对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性大小,并把这个常数称为随机事件A的概率,记作P(A)随机事件的概率定义理解:注意点:1.事件A的概率范围即随机事件发生的概率都满足:0
(2)区别:例1. ①明天的下雨概率是60%是指( )
A.明天有60%的时间下雨
B.假如天气条件相同的天数是100天,那么恰好有60天要下雨
C.明天下雨的可能性是60%
D.明天有60%的地方要下雨 C例1. ②某医院治疗一种疾病的治愈率为10%, 那么前9个病人都没有治愈,第10个病人就一定能治愈,试从概率的角度解释这说法是否正确?答:不正确.
如果把治疗一个病人作为一次试验,治愈率为10%, 是指随着试验次数的增加,即治疗病人的增加,大约有10%的人能够治愈, 对于一次试验来说,其结果是随机的,因此前9个病人都没有治愈是可能的,对第10个病人来说,其结果仍然是随机的,即有可能治愈,也有可能没有治愈.治愈的可能性为10%.例2.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(1)试计算男婴各年出生频率(精确到0.001);
(2)该市男婴出生的概率约是多少?(1)1999年男婴出生的频率为:解题示范:同理可求得2000年、2001年和2002年男婴出生的频率分别为:0.521,0.512,0.512.(2) 各年男婴出生的频率在0.51~0.53之间,各频率都在0.52附近摆动,故该市男婴出生的概率约是0.52.1、指出下列事件是必然事件,不可能事件还是随机事件?(1)我国东南沿海某地明年将3次受到热带气旋的侵袭;
(2)若a为实数,则|a+1|+|a+2|=0;
(3)江苏地区每年1月份月平均气温低于7月份月平均气温;
(4)发射1枚炮弹,命中目标.练一练随机事件随机事件不可能事件必然事件BC4、某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能
投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 但可以说明的是:投10次篮,投中8次的可能性最大,即概率越大,事件发生的可能性越大.概率约是0.80.780.750.800.80 0.85 0.830.80做这种统计有意义吗? 密码破解:
我们随便找一个英语单词,比如cat,将每个字母向后移动一位,cat变成dbu,将每个字母向后移动两位,cat变成ecv,等等,这就是一种最原始、最简单的加密方法,19世纪以前曾在欧洲广泛使用.
但后来人们就利用了字母出现频率的多少,轻易破解了这种方法:利用字母e出现频率最高,大多数单词中都包含它的特征,观察加密电文中,出现次数最多的字母,假如是h,则就可以断定h就是e,原文的每个字母都向后移动了三位(e-f-g-h),因此只要将每个字母向前移动三位,即可看到明文. 做这种统计有意义吗? 男女出生率的研究:
一般人或许认为:生男生女的可能性是相等的,因而推测出男婴和女婴的出生数的比因当是1:1,可事实并非如此.
公元1814年,法国数学家拉普拉斯在他的新作<<概率的哲学探讨>>一书中,记载了一下有趣的统计.他根据伦敦,彼得堡,柏林和全法国的统计资料,得出了几乎完全一致的男婴和女婴出生数的比值是22:21,即在全体出生婴儿中,男婴占51.16%,女婴占48.84%.可奇怪的是,当他统计1745---1784整整四十年间巴黎男婴出生率时,却得到了另一个比是25:24,男婴占51.02%,与前者相差0.14%. 这千分之一点四的后面,隐藏了什么?拉普拉斯深入进行调查研究,终于发现:当时巴黎人”重女轻男”,又抛弃男婴的陋俗,以至于歪曲了出生率的真相!做这种统计有意义吗? 弗格森发现尚克斯关于π值计算中的错误;天气预报的改变;《红楼梦》作者的考证;…回顾小结:随机事件及其概率事件的含义事件的分类事件的表示频率与概率课后作业:课本 P91 习题3.1
No.1、2、3、5.
