2.3.1 平面向量基本定理(15张)
文档属性
| 名称 | 2.3.1 平面向量基本定理(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 00:00:00 | ||
图片预览



文档简介
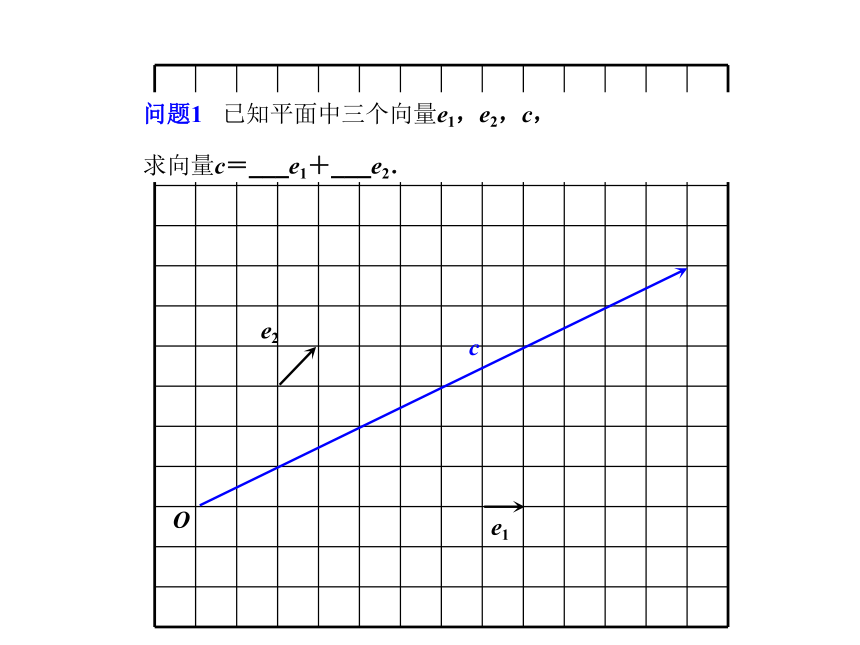
课件15张PPT。高中数学 必修42.3.1 平面向量基本定理 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v''v=vx+vy=6i+4je1e2cO问题1 已知平面中三个向量e1,e2,c,
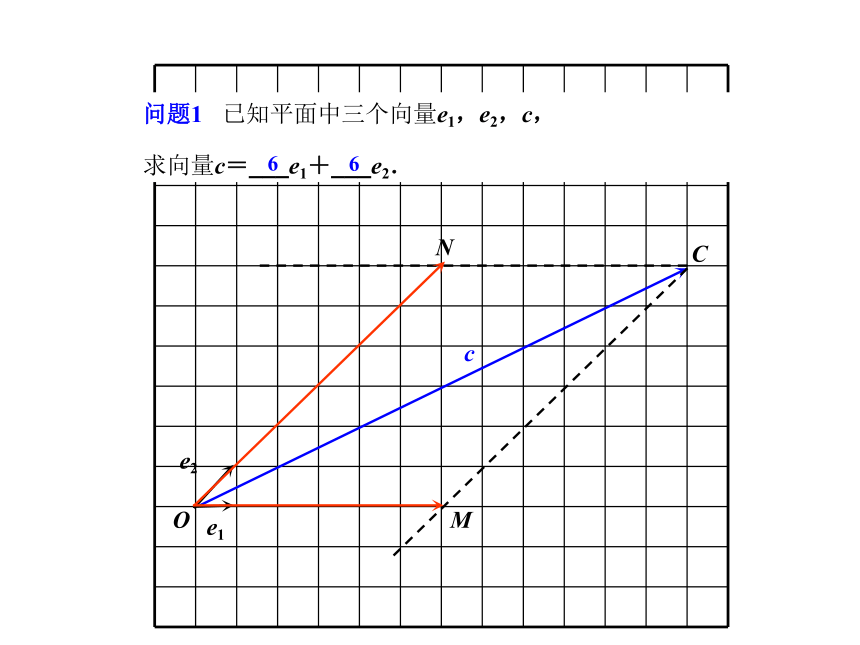
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
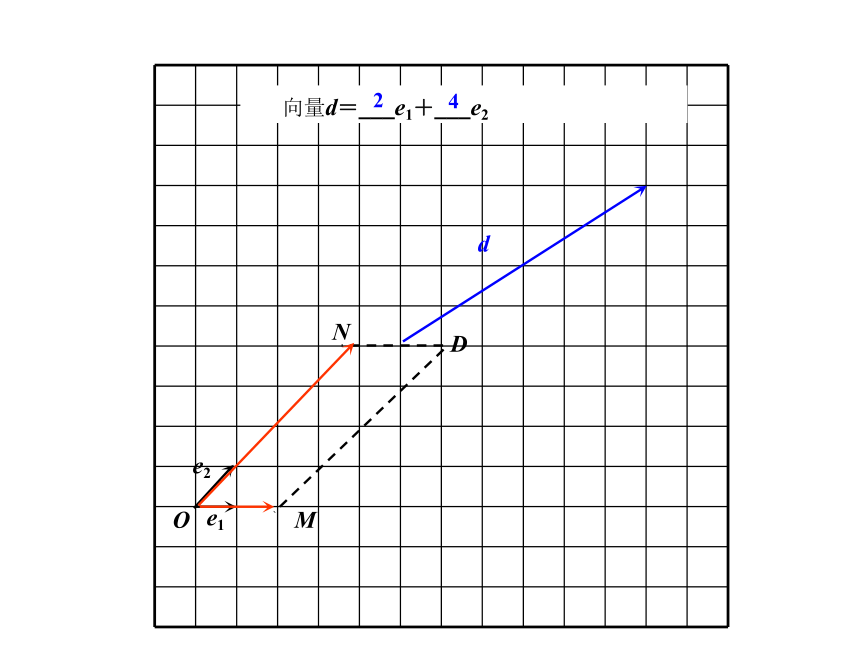
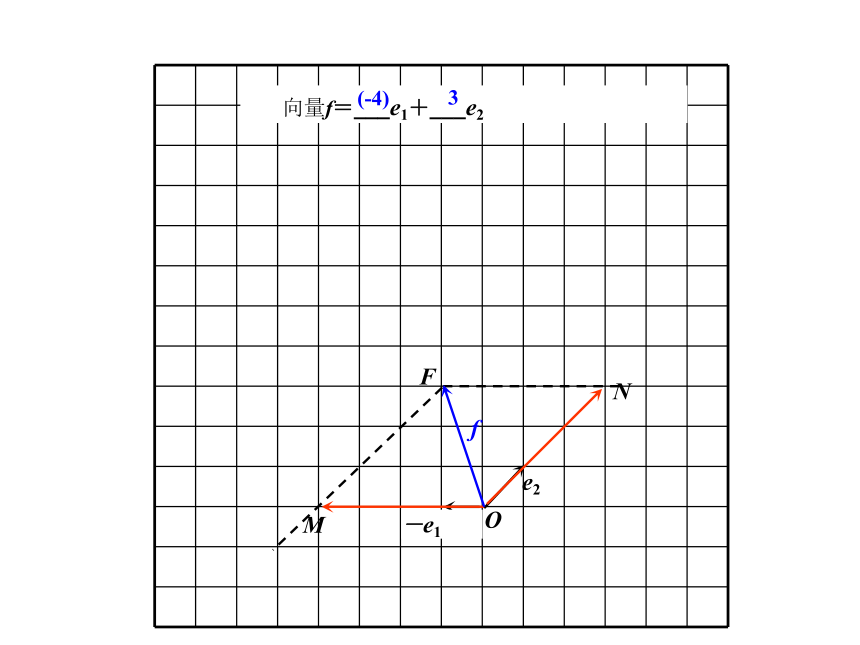
求向量c=___e1+___e2.66 向量d=___e1+___e2OMN24e1e2D 向量f=___e1+___e2e2e1F-e1OMNf 向量f=___e1+___e2(-4)3e2FOe1e2问题2 如果e1,e2是平面内任意两向量,那么平面内的任一向量a还可以表示成a=?1e1+?2e2的形式吗?e2a平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;(2)一个平面向量用一组基底e1,e2表示成 a=?1e1+?2e2的形式,我
们称它为向量的分解. 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习:B例1 如图所示,平行四边形ABCD的两条对角线相交于点M,且
AB=a,AD=b,用a,b表示MA,MB,MC,MD.ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:EF 平面向量基本定理,其实质在于:同一平面内任一向量都可以表示为两个不共线向量e1,e2的线性组合,且e1,e2是这一平面内所有向量的一组基底. 小结:
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.66 向量d=___e1+___e2OMN24e1e2D 向量f=___e1+___e2e2e1F-e1OMNf 向量f=___e1+___e2(-4)3e2FOe1e2问题2 如果e1,e2是平面内任意两向量,那么平面内的任一向量a还可以表示成a=?1e1+?2e2的形式吗?e2a平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;(2)一个平面向量用一组基底e1,e2表示成 a=?1e1+?2e2的形式,我
们称它为向量的分解. 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习:B例1 如图所示,平行四边形ABCD的两条对角线相交于点M,且
AB=a,AD=b,用a,b表示MA,MB,MC,MD.ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:EF 平面向量基本定理,其实质在于:同一平面内任一向量都可以表示为两个不共线向量e1,e2的线性组合,且e1,e2是这一平面内所有向量的一组基底. 小结:
