1.2 余弦定理(15张)
图片预览





文档简介
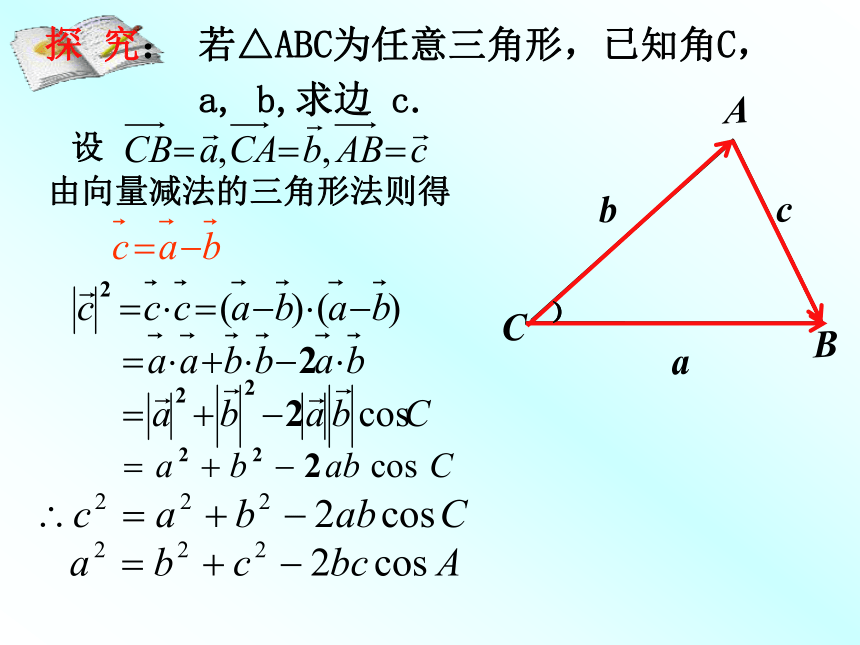
课件15张PPT。正弦定理:可以解决两类有关三角形的问题?(1)已知两角和任一边。(2)已知两边和一边的对角。变形:复习回顾余弦定理CBAcab﹚﹚探 究: 若△ABC为任意三角形,已知角C,
a, b,求边 c.设由向量减法的三角形法则得CBAcab﹚余弦定理由向量减法的三角形法则得探 究: 若△ABC为任意三角形,已知角C,
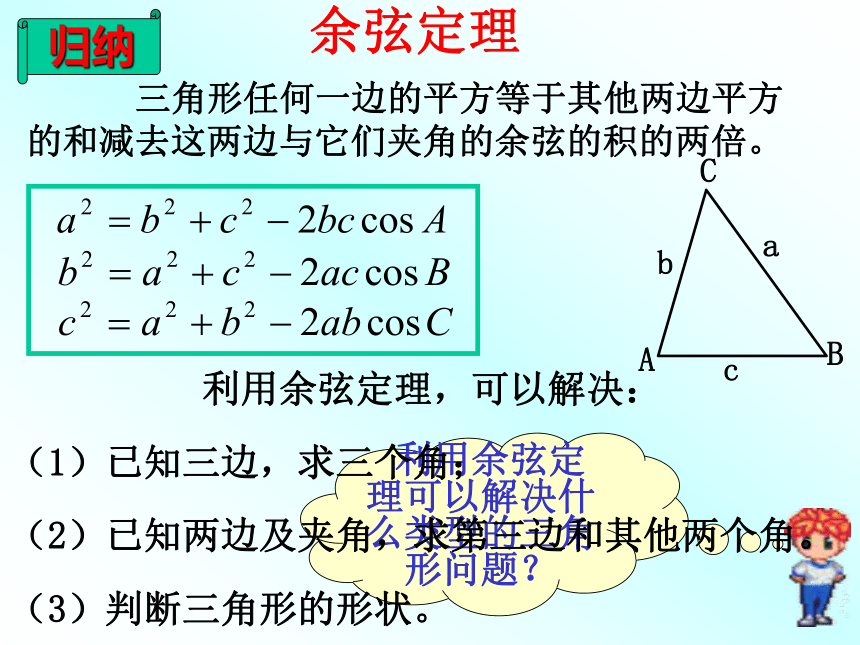
a, b,求边 c.设向量法余弦定理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 利用余弦定理可以解决什么类型的三角形问题?归纳 利用余弦定理,可以解决:
(1)已知三边,求三个角;
(2)已知两边及夹角,求第三边和其他两个角。
(3)判断三角形的形状。余弦定理 已知三边,怎样求三个角呢?推论:思考1:一、已知三角形的两边及夹角求解三角形变式:例2、在△ABC中,已知a= ,b=2,c= ,
解三角形(依次求解A、B、C).解:由余弦定理得二、已知三角函数的三边解三角形变式: 由推论我们能判断三角形的角的情况吗?推论:思考2:提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形例3、在△ABC中,若 ,
则△ABC的形状为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定那 呢?三、判断三角形的形状三角形三边长分别为4,6,8,则此三角形为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定思考: 已知两边及一边的对角时,想一想如何来解这个三角形?
如:已知b=4,c= ,C=60°求边a.小结: 余弦定理可以解决的有关三角形的问题:
1、已知两边及其夹角,求第三边和其他两个角。
2、已知三边求三个角;
3、判断三角形的形状余弦定理:推论:
a, b,求边 c.设由向量减法的三角形法则得CBAcab﹚余弦定理由向量减法的三角形法则得探 究: 若△ABC为任意三角形,已知角C,
a, b,求边 c.设向量法余弦定理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 利用余弦定理可以解决什么类型的三角形问题?归纳 利用余弦定理,可以解决:
(1)已知三边,求三个角;
(2)已知两边及夹角,求第三边和其他两个角。
(3)判断三角形的形状。余弦定理 已知三边,怎样求三个角呢?推论:思考1:一、已知三角形的两边及夹角求解三角形变式:例2、在△ABC中,已知a= ,b=2,c= ,
解三角形(依次求解A、B、C).解:由余弦定理得二、已知三角函数的三边解三角形变式: 由推论我们能判断三角形的角的情况吗?推论:思考2:提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形例3、在△ABC中,若 ,
则△ABC的形状为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定那 呢?三、判断三角形的形状三角形三边长分别为4,6,8,则此三角形为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定思考: 已知两边及一边的对角时,想一想如何来解这个三角形?
如:已知b=4,c= ,C=60°求边a.小结: 余弦定理可以解决的有关三角形的问题:
1、已知两边及其夹角,求第三边和其他两个角。
2、已知三边求三个角;
3、判断三角形的形状余弦定理:推论:
