人教版高中数学必修五第3章不等式3.4基本不等式(教师版)
文档属性
| 名称 | 人教版高中数学必修五第3章不等式3.4基本不等式(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 953.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-10 16:18:39 | ||
图片预览


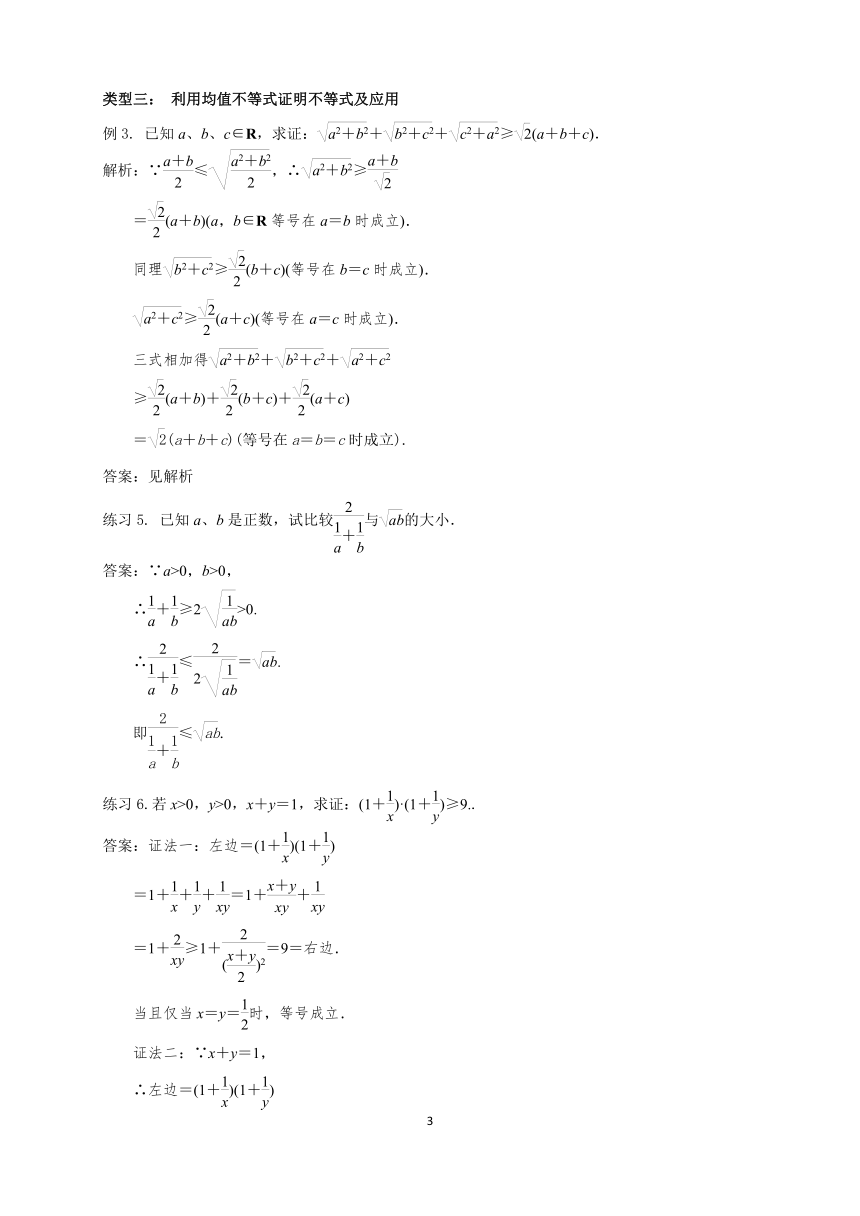


文档简介
基本不等式
(均值不等式)
__________________________________________________________________________________
__________________________________________________________________________________
教学重点: 掌握均值不等式的证明及应用,会用均值不等式求函数的最大值或最小值;
教学难点: 利用均值不等式的证明。
算术平均值与几何平均值
算术平均值:对任意两个正实数,数 叫做的算术平均值
几何平均值:对任意两个正实数,数叫做的几何平均值
均值定理
如果,那么,当且仅当时,等号成立
均值不等式的常见变形
(1)
(2)
(3)(同号且不为0)
(4)
类型一: 均值不等式的理解
设,则下列不等式不成立的是()
A. B. C. D.
解析:特值法,令,则A,B,C项都成立,而D项中, 显然不成立,故D项不成立。
答案:D
练习1. 若a、b∈R,且ab>0,则下列不等式中,恒成立的是( )
A.a2+b2>2ab B.a+b≥2 C.+> D.+≥2
答案:D
练习2. 设0A.a答案:B
类型二: 均值不等式与最值
例2. 若正数x、y满足x+3y=5xy,则3x+4y的最小值是( )
A. B. C.5 D.6
解析:由x+3y=5xy得+=1,∴3x+4y=(3x+4y)·(+)=+++≥2+=+=5,当且仅当=时,得到最小值5.
答案:C
练习3. 设x、y∈R,且x+y=5,则3x+3y的最小值为( )
A.10 B.6 C.4 D.18
答案:D
练习4. 已知正项等差数列{an}中,a5+a16=10则a5a16的最大值为( )
A.100 B.75 C.50 D.25
答案:D
类型三: 利用均值不等式证明不等式及应用
例3. 已知a、b、c∈R,求证:++≥(a+b+c).
解析:∵≤,∴≥
=(a+b)(a,b∈R等号在a=b时成立).
同理≥(b+c)(等号在b=c时成立).
≥(a+c)(等号在a=c时成立).
三式相加得++
≥(a+b)+(b+c)+(a+c)
=(a+b+c)(等号在a=b=c时成立).
答案:见解析
练习5. 已知a、b是正数,试比较与的大小.
答案:∵a>0,b>0,
∴+≥2>0.
∴≤=.
即≤.
练习6.若x>0,y>0,x+y=1,求证:(1+)·(1+)≥9..
答案:证法一:左边=(1+)(1+)
=1+++=1++
=1+≥1+=9=右边.
当且仅当x=y=时,等号成立.
证法二:∵x+y=1,
∴左边=(1+)(1+)
=(1+)(1+)=(2+)(2+)
=5+2(+)≥5+4=9=右边.
当且仅当x=y=时,等号成立.
例4. 在面积为S(S为定值)的扇形中,当扇形中心角为θ,半径为r时,扇形周长最小,这时θ、r的值分别是( )
A.θ=1,r= B.θ=2,r= C.θ=2,r= D.θ=2,r=
解析:S=θr2?θ=,
又扇形周长P=2r+θr=2≥4,
当P最小时,r=?r=,此时θ=2.
答案:D
练习7. 设计用32m2的材料制造某种长方体车厢(无盖),按交通规定车厢宽为2m,则车厢的最大容积是( )
A.(38-3)m3 B.16m3 C.4m3 D.14m3
答案:B
练习8. 将进货单价为80元的商品按90元一个售出时,能卖出400个,每涨价1元,其销售量就减少20个,为获得最大利润,售价应定在( )
A.每个95元 B.每个100元 C.每个105元 D.每个110元
答案:A
1. 若x>0,y>0,且x+y≤4,则下列不等式中恒成立的是( )
A.≤ B.+≥1 C.≥2 D.≥1
答案:B
2. 已知m、n∈R,m2+n2=100,则mn的最大值是( )
A.100 B.50 C.20 D.10
答案:B
3. 若a>0,b>0且a+b=4,则下列不等式恒成立的是( )
A.> B.+≤1 C.≥2 D.≤
答案:D
4. 实数x、y满足x+2y=4,则3x+9y的最小值为( )
A.18 B.12 C.2 D.
答案:A
5.设x+3y-2=0,则3x+27y+1的最小值为( )
A.7 B.3 C.1+2 D.5
答案:A
6. 设a>0,b>0,若是3a与3b的等比中项,则+的最小值为( )
A.8 B.4 C.1 D.
答案:B
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 若0A.a2+b2 B.2 C.2ab D.a+b
答案:D
2. 若2x+2y=1,则x+y的取值范围是( )
A.[0,2] B.[-2,0] C.[-2,+∞) D.(-∞,-2]
答案:D
3. 已知x、y∈R+,且满足+=1,则xy的最大值为________.
答案:3
4. 已知a、b为实常数,函数y=(x-a)2+(x-b)2的最小值为__________
答案:(a-b)2
5. a、b、c是互不相等的正数,且a2+c2=2bc,则下列关系中可能成立的是( )
A.a>b>c B.c>a> b C.b>a>c D.a>c>b
答案:C
6. 设{an}是正数等差数列,{bn}是正数等比数列,且a1=b1,a21=b21,则( )
A.a11=b11 B.a11>b11 C.a11答案:D
7. 已知a>1,b>1,且lga+lgb=6,则lga·lgb的最大值为( )
A.6 B.9 C.12 D.18
答案:B
8. 某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
A.60件 B.80件 C.100件 D.120件
答案:B
9. 已知+=2(x>0,y>0),则xy的最小值是________.
答案:6
10. 若实数x、y满足x2+y2+xy=1,则x+y的最大值是________.
答案:
11. 做一个面积为1 m2,形状为直角三角形的铁架框,在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
答案:C
12. 光线透过一块玻璃,其强度要减弱.要使光线的强度减弱到原来的以下,至少需这样的玻璃板________块.(参考数据:lg2=0.3010,lg3=0.4771)
答案:11
13. 一个矩形的周长为l,面积为S,给出下列实数对:①(4,1);②(8,6);③(10,8);④(3,).其中可作为(l,S)的取值的实数对的序号是________.
答案:①④
14. 已知正常数a、b和正实数x、y,满足a+b=10,+=1,x+y的最小值为18,求a、b的值.
答案:x+y=(x+y)·1=(x+y)·(+)
=a+b++≥a+b+2=(+)2,
等号在=即=时成立.
∴x+y的最小值为(+)2=18,
又a+b=10,∴ab=16.
∴a、b是方程x2-10x+16=0的两根,
∴a=2,b=8或a=8,b=2.
能力提升
15. 已知x>0,y>0,lg2x+lg8y=lg2,则 +的最小值是( )
A.2 B.2 C.4 D.2
答案:C
16. 设函数f(x)=2x+-1(x<0),则f(x)( )
A.有最大值 B.有最小值 C.是增函数 D.是减函数
答案:A
17. 已知x>0,y>0,x、a、b、y成等差数列,x、c、d、y成等比数列,则的最小值是( )
A.0 B.1 C.2 D.4
答案:D
18. 若a、b、c、d、x、y是正实数,且P=+,Q=·,则有( )
A.P=Q B.P≥Q C.P≤Q D.P>Q
答案:C
19. 已知x≥,则f(x)=有( )
A.最大值 B.最小值 C.最大值1 D.最小值1
答案: D
20. 已知y>x>0,且x+y=1,那么( )
A.x<答案:D
21. 设a、b是正实数,给出以下不等式:
①>;②a>|a-b|-b;③a2+b2>4ab-3b2;④ab+>2,其中恒成立的序号为( )
A.①③ B.①④ C.②③ D.②④
答案:D
22. 已知a>0,b>0,且a+b=1,则的最小值为( )
A.6 B.7 C.8 D.9
答案:D
23.若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则+的最小值为( )
A. B. C.2 D.4
答案:D
24. 当x>1时,不等式x+≥a恒成立,则实数a的取值范围是( )
A.(-∞,2] B.[2,+∞) C.[3,+∞) D.(-∞,3]
答案:D
25. 已知正数x、y满足+=1,则xy有( )
A.最小值 B.最大值16 C.最小值16 D.最大值
答案:C
26. 若正实数x、y满足2x+y+6=xy,则xy的最小值是________
答案:18
27. 已知函数f(x)=lgx(x∈R+),若x1、x2∈R+,判断[f(x1)+f(x2)]与f()的大小并加以证明.
答案:[f(x1)+f(x2)]≤f()
∵f(x1)+f(x2)=lgx1+lgx2=lg(x1·x2),
f()=lg,
而x1、x2∈R+,x1x2≤()2,
而f(x)=lgx在区间(0,+∞)上为增函数.
∴lg(x1x2)≤lg()2,
∴lg(x1x2)≤lg.
即(lgx1+lgx2)≤lg.
因此,[f(x1)+f(x2)]≤f().
28. 已知a、b、c∈R+,求证:++≥a+b+C
答案:∵a、b、c∈R+,,,均大于0,
又+b≥2=2a,
+c≥2=2b,
+a≥2=2c,
三式相加得+b++c++a≥2a+2b+2c,
∴++≥a+b+C.
29.求函数y=1-2x-的值域.
答案:y=1-2x-=1-(2x+).
①当x>0时,2x+≥2=2.
当且仅当2x=,即x=时取等号.
∴y=1-(2x+)≤1-2.
②当x<0时,y=1+(-2x)+(-).
∵-2x+(-)≥2=2.
当且仅当-2x=-时,即x=-时取等号.
∴此时y=1-2x-≥1+2
综上知y∈(-∞,1-2]∪[1+2,+∞).
∴函数y=1-2x-的值域为(-∞,1-2)∪[1+2,+∞).
30. 某单位决定投资3 200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元.试求:
(1)仓库面积S的取值范围是多少?
(2)为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计多长?
答案:(1)设正面铁栅长x m,侧面长为y m,总造价为z元,则z=40x+2×45y+20xy=40x+90y+20xy,仓库面积S=xy.
由条件知z≤3 200,即4x+9y+2xy≤320.
∵x>0,y>0,
∴4x+9y≥2=12.
∴6+S≤160,即()2+6-160≤0.
∴0<≤10,∴0故S的取值范围是(0,100].
(2)当S=100 m2时,4x=9y,且xy=100.
解之得x=15(m),y=(m).
答:仓库面积S的取值范围是(0,100],当S取到最大允许值100 m2时,正面铁栅长15 m.
31. 某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算?
答案:由题设知每年的费用是以12为首项,4为公差的等差数列.设纯收入与年数的关系为f(n),则
f(n)=50n-[12+16+…+(8+4n)]-98=40n-2n2-98.
(1)由f(n)>0得,n2-20n+49<0,
∴10-又∵n∈N,∴n=3,4,…,17.
即从第3年开始获利.
(2)①年平均收入==40-2(n+)≤40-2×14=12,
当且仅当n=7时,渔船总收益为12×7+26=110(万元).
②f(n)=-2(n-10)2+102.
因此当n=10时,f(n)max=102,总收益为102+8=110万元,但7<10,所以第一种方案更合算.
1
(均值不等式)
__________________________________________________________________________________
__________________________________________________________________________________
教学重点: 掌握均值不等式的证明及应用,会用均值不等式求函数的最大值或最小值;
教学难点: 利用均值不等式的证明。
算术平均值与几何平均值
算术平均值:对任意两个正实数,数 叫做的算术平均值
几何平均值:对任意两个正实数,数叫做的几何平均值
均值定理
如果,那么,当且仅当时,等号成立
均值不等式的常见变形
(1)
(2)
(3)(同号且不为0)
(4)
类型一: 均值不等式的理解
设,则下列不等式不成立的是()
A. B. C. D.
解析:特值法,令,则A,B,C项都成立,而D项中, 显然不成立,故D项不成立。
答案:D
练习1. 若a、b∈R,且ab>0,则下列不等式中,恒成立的是( )
A.a2+b2>2ab B.a+b≥2 C.+> D.+≥2
答案:D
练习2. 设0
类型二: 均值不等式与最值
例2. 若正数x、y满足x+3y=5xy,则3x+4y的最小值是( )
A. B. C.5 D.6
解析:由x+3y=5xy得+=1,∴3x+4y=(3x+4y)·(+)=+++≥2+=+=5,当且仅当=时,得到最小值5.
答案:C
练习3. 设x、y∈R,且x+y=5,则3x+3y的最小值为( )
A.10 B.6 C.4 D.18
答案:D
练习4. 已知正项等差数列{an}中,a5+a16=10则a5a16的最大值为( )
A.100 B.75 C.50 D.25
答案:D
类型三: 利用均值不等式证明不等式及应用
例3. 已知a、b、c∈R,求证:++≥(a+b+c).
解析:∵≤,∴≥
=(a+b)(a,b∈R等号在a=b时成立).
同理≥(b+c)(等号在b=c时成立).
≥(a+c)(等号在a=c时成立).
三式相加得++
≥(a+b)+(b+c)+(a+c)
=(a+b+c)(等号在a=b=c时成立).
答案:见解析
练习5. 已知a、b是正数,试比较与的大小.
答案:∵a>0,b>0,
∴+≥2>0.
∴≤=.
即≤.
练习6.若x>0,y>0,x+y=1,求证:(1+)·(1+)≥9..
答案:证法一:左边=(1+)(1+)
=1+++=1++
=1+≥1+=9=右边.
当且仅当x=y=时,等号成立.
证法二:∵x+y=1,
∴左边=(1+)(1+)
=(1+)(1+)=(2+)(2+)
=5+2(+)≥5+4=9=右边.
当且仅当x=y=时,等号成立.
例4. 在面积为S(S为定值)的扇形中,当扇形中心角为θ,半径为r时,扇形周长最小,这时θ、r的值分别是( )
A.θ=1,r= B.θ=2,r= C.θ=2,r= D.θ=2,r=
解析:S=θr2?θ=,
又扇形周长P=2r+θr=2≥4,
当P最小时,r=?r=,此时θ=2.
答案:D
练习7. 设计用32m2的材料制造某种长方体车厢(无盖),按交通规定车厢宽为2m,则车厢的最大容积是( )
A.(38-3)m3 B.16m3 C.4m3 D.14m3
答案:B
练习8. 将进货单价为80元的商品按90元一个售出时,能卖出400个,每涨价1元,其销售量就减少20个,为获得最大利润,售价应定在( )
A.每个95元 B.每个100元 C.每个105元 D.每个110元
答案:A
1. 若x>0,y>0,且x+y≤4,则下列不等式中恒成立的是( )
A.≤ B.+≥1 C.≥2 D.≥1
答案:B
2. 已知m、n∈R,m2+n2=100,则mn的最大值是( )
A.100 B.50 C.20 D.10
答案:B
3. 若a>0,b>0且a+b=4,则下列不等式恒成立的是( )
A.> B.+≤1 C.≥2 D.≤
答案:D
4. 实数x、y满足x+2y=4,则3x+9y的最小值为( )
A.18 B.12 C.2 D.
答案:A
5.设x+3y-2=0,则3x+27y+1的最小值为( )
A.7 B.3 C.1+2 D.5
答案:A
6. 设a>0,b>0,若是3a与3b的等比中项,则+的最小值为( )
A.8 B.4 C.1 D.
答案:B
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 若0
答案:D
2. 若2x+2y=1,则x+y的取值范围是( )
A.[0,2] B.[-2,0] C.[-2,+∞) D.(-∞,-2]
答案:D
3. 已知x、y∈R+,且满足+=1,则xy的最大值为________.
答案:3
4. 已知a、b为实常数,函数y=(x-a)2+(x-b)2的最小值为__________
答案:(a-b)2
5. a、b、c是互不相等的正数,且a2+c2=2bc,则下列关系中可能成立的是( )
A.a>b>c B.c>a> b C.b>a>c D.a>c>b
答案:C
6. 设{an}是正数等差数列,{bn}是正数等比数列,且a1=b1,a21=b21,则( )
A.a11=b11 B.a11>b11 C.a11
7. 已知a>1,b>1,且lga+lgb=6,则lga·lgb的最大值为( )
A.6 B.9 C.12 D.18
答案:B
8. 某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
A.60件 B.80件 C.100件 D.120件
答案:B
9. 已知+=2(x>0,y>0),则xy的最小值是________.
答案:6
10. 若实数x、y满足x2+y2+xy=1,则x+y的最大值是________.
答案:
11. 做一个面积为1 m2,形状为直角三角形的铁架框,在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
答案:C
12. 光线透过一块玻璃,其强度要减弱.要使光线的强度减弱到原来的以下,至少需这样的玻璃板________块.(参考数据:lg2=0.3010,lg3=0.4771)
答案:11
13. 一个矩形的周长为l,面积为S,给出下列实数对:①(4,1);②(8,6);③(10,8);④(3,).其中可作为(l,S)的取值的实数对的序号是________.
答案:①④
14. 已知正常数a、b和正实数x、y,满足a+b=10,+=1,x+y的最小值为18,求a、b的值.
答案:x+y=(x+y)·1=(x+y)·(+)
=a+b++≥a+b+2=(+)2,
等号在=即=时成立.
∴x+y的最小值为(+)2=18,
又a+b=10,∴ab=16.
∴a、b是方程x2-10x+16=0的两根,
∴a=2,b=8或a=8,b=2.
能力提升
15. 已知x>0,y>0,lg2x+lg8y=lg2,则 +的最小值是( )
A.2 B.2 C.4 D.2
答案:C
16. 设函数f(x)=2x+-1(x<0),则f(x)( )
A.有最大值 B.有最小值 C.是增函数 D.是减函数
答案:A
17. 已知x>0,y>0,x、a、b、y成等差数列,x、c、d、y成等比数列,则的最小值是( )
A.0 B.1 C.2 D.4
答案:D
18. 若a、b、c、d、x、y是正实数,且P=+,Q=·,则有( )
A.P=Q B.P≥Q C.P≤Q D.P>Q
答案:C
19. 已知x≥,则f(x)=有( )
A.最大值 B.最小值 C.最大值1 D.最小值1
答案: D
20. 已知y>x>0,且x+y=1,那么( )
A.x<
21. 设a、b是正实数,给出以下不等式:
①>;②a>|a-b|-b;③a2+b2>4ab-3b2;④ab+>2,其中恒成立的序号为( )
A.①③ B.①④ C.②③ D.②④
答案:D
22. 已知a>0,b>0,且a+b=1,则的最小值为( )
A.6 B.7 C.8 D.9
答案:D
23.若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则+的最小值为( )
A. B. C.2 D.4
答案:D
24. 当x>1时,不等式x+≥a恒成立,则实数a的取值范围是( )
A.(-∞,2] B.[2,+∞) C.[3,+∞) D.(-∞,3]
答案:D
25. 已知正数x、y满足+=1,则xy有( )
A.最小值 B.最大值16 C.最小值16 D.最大值
答案:C
26. 若正实数x、y满足2x+y+6=xy,则xy的最小值是________
答案:18
27. 已知函数f(x)=lgx(x∈R+),若x1、x2∈R+,判断[f(x1)+f(x2)]与f()的大小并加以证明.
答案:[f(x1)+f(x2)]≤f()
∵f(x1)+f(x2)=lgx1+lgx2=lg(x1·x2),
f()=lg,
而x1、x2∈R+,x1x2≤()2,
而f(x)=lgx在区间(0,+∞)上为增函数.
∴lg(x1x2)≤lg()2,
∴lg(x1x2)≤lg.
即(lgx1+lgx2)≤lg.
因此,[f(x1)+f(x2)]≤f().
28. 已知a、b、c∈R+,求证:++≥a+b+C
答案:∵a、b、c∈R+,,,均大于0,
又+b≥2=2a,
+c≥2=2b,
+a≥2=2c,
三式相加得+b++c++a≥2a+2b+2c,
∴++≥a+b+C.
29.求函数y=1-2x-的值域.
答案:y=1-2x-=1-(2x+).
①当x>0时,2x+≥2=2.
当且仅当2x=,即x=时取等号.
∴y=1-(2x+)≤1-2.
②当x<0时,y=1+(-2x)+(-).
∵-2x+(-)≥2=2.
当且仅当-2x=-时,即x=-时取等号.
∴此时y=1-2x-≥1+2
综上知y∈(-∞,1-2]∪[1+2,+∞).
∴函数y=1-2x-的值域为(-∞,1-2)∪[1+2,+∞).
30. 某单位决定投资3 200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元.试求:
(1)仓库面积S的取值范围是多少?
(2)为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计多长?
答案:(1)设正面铁栅长x m,侧面长为y m,总造价为z元,则z=40x+2×45y+20xy=40x+90y+20xy,仓库面积S=xy.
由条件知z≤3 200,即4x+9y+2xy≤320.
∵x>0,y>0,
∴4x+9y≥2=12.
∴6+S≤160,即()2+6-160≤0.
∴0<≤10,∴0
(2)当S=100 m2时,4x=9y,且xy=100.
解之得x=15(m),y=(m).
答:仓库面积S的取值范围是(0,100],当S取到最大允许值100 m2时,正面铁栅长15 m.
31. 某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算?
答案:由题设知每年的费用是以12为首项,4为公差的等差数列.设纯收入与年数的关系为f(n),则
f(n)=50n-[12+16+…+(8+4n)]-98=40n-2n2-98.
(1)由f(n)>0得,n2-20n+49<0,
∴10-
即从第3年开始获利.
(2)①年平均收入==40-2(n+)≤40-2×14=12,
当且仅当n=7时,渔船总收益为12×7+26=110(万元).
②f(n)=-2(n-10)2+102.
因此当n=10时,f(n)max=102,总收益为102+8=110万元,但7<10,所以第一种方案更合算.
1
