人教版高中数学选修2-1第三章空间向量与立体几何3.1空间向量及其运算(教师版)【个性化辅导含答案】
文档属性
| 名称 | 人教版高中数学选修2-1第三章空间向量与立体几何3.1空间向量及其运算(教师版)【个性化辅导含答案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-10 16:27:30 | ||
图片预览



文档简介
空间向量及其运算
__________________________________________________________________________________
__________________________________________________________________________________
1 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示;
2 掌握空间向量的线性运算及其坐标表示;
3 掌握空间向量的数量积及其坐标表示,能用向量的数量积判断向量的共线和垂直.
1.空间向量的有关概念
名称 概念 表示
零向量 模为0的向量 0
单位向量 长度(模)为1的向量
相等向量 方向相同且模相等的向量 a=b
相反向量 方向相反且模相等的向量 a的相反向量为-a
共线向量 表示空间向量的有向线段所在的直线互相平行或重合 a∥b
共面向量 平行于同一个平面的向量
2.共线向量、共面向量定理和空间向量基本定理
(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使得a=λb.
(2)共面向量定理:若两个向量a,b不共线,则向量p与向量a,b共面?存在唯一的有序实数对(x,y),使p=xa+yb.
(3)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc,把{a,b,c}叫做空间的一个基底.
3.空间向量的数量积及运算律
(1)数量积及相关概念
①两向量的夹角
已知两个非零向量a,b,在空间任取一点O,作=a,=b,则∠AOB叫做向量a与b的夹角,记作〈a,b〉,其范围是0≤〈a,b〉≤π,若〈a,b〉=,则称a与b互相垂直,记作a⊥b.
②两向量的数量积
已知空间两个非零向量a,b,则|a||b|cos〈a,b〉叫做向量a,b的数量积,记作a·b,即a·b=|a||b|cos〈a,b〉.
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
③分配律:a·(b+c)=a·b+a·c.
4.空间向量的坐标表示及其应用
设a=(a1,a2,a3),b=(b1,b2,b3).
向量表示[ 坐标表示
数量积 a·b a1b1+a2b2+a3b3
共线 a=λb(b≠0) a1=λb1,a2=λb2,a3=λb3
垂直 a·b=0 (a≠0,b≠0) a1b1+a2b2+a3b3=0
模 |a|
夹角 〈a,b〉(a≠0,b≠0) cos〈a,b〉=
规律方法:
1.选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决立体几何问题的基本要求.如本例用,,表示,等,另外解题时应结合已知和所求观察图形,联想相关的运算法则和公式等,就近表示所需向量.
(2.首尾相接的若干个向量的和,等于由起始向量的起点指向末尾向量的终点的向量.所以在求若干向量的和,可以通过平移将其转化为首尾相接的向量求和.
3.数量积的应用:
求夹角,设向量a,b所成的角为θ,则cosθ=,进而可求两异面直线所成的角;
(2)求长度(距离),运用公式|a|2=a·a,可使线段长度的计算问题转化为向量数量积的计算问题;(3)解决垂直问题,利用a⊥ba·b=0(a≠0,b≠0),可将垂直问题转化为向量数量积的计算问题.
类型一 空间向量的线性运算
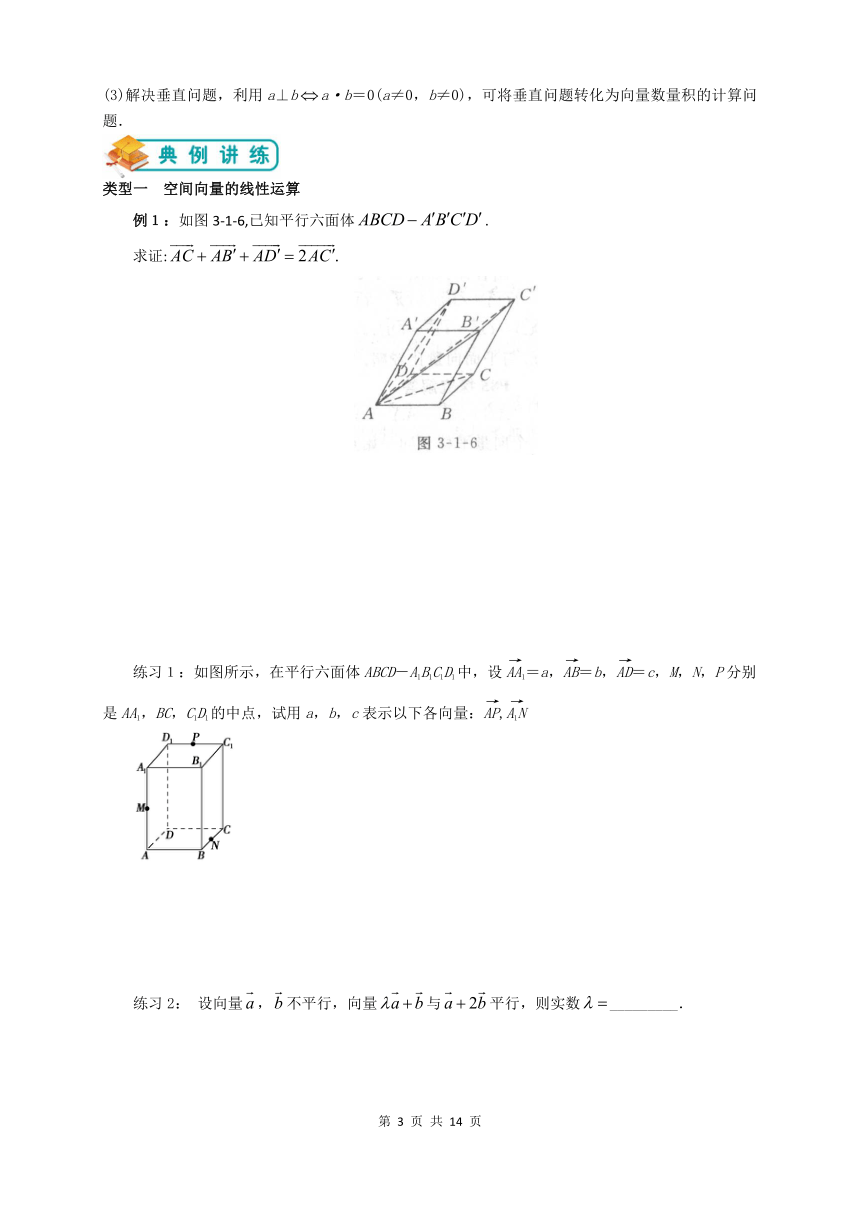
例1:如图3-1-6,已知平行六面体.
求证:
练习1:如图所示,在平行六面体ABCD-A1B1C1D1中,设1=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:,
练习2: 设向量,不平行,向量与平行,则实数_________.
类型二 共线定理、共面定理的应用
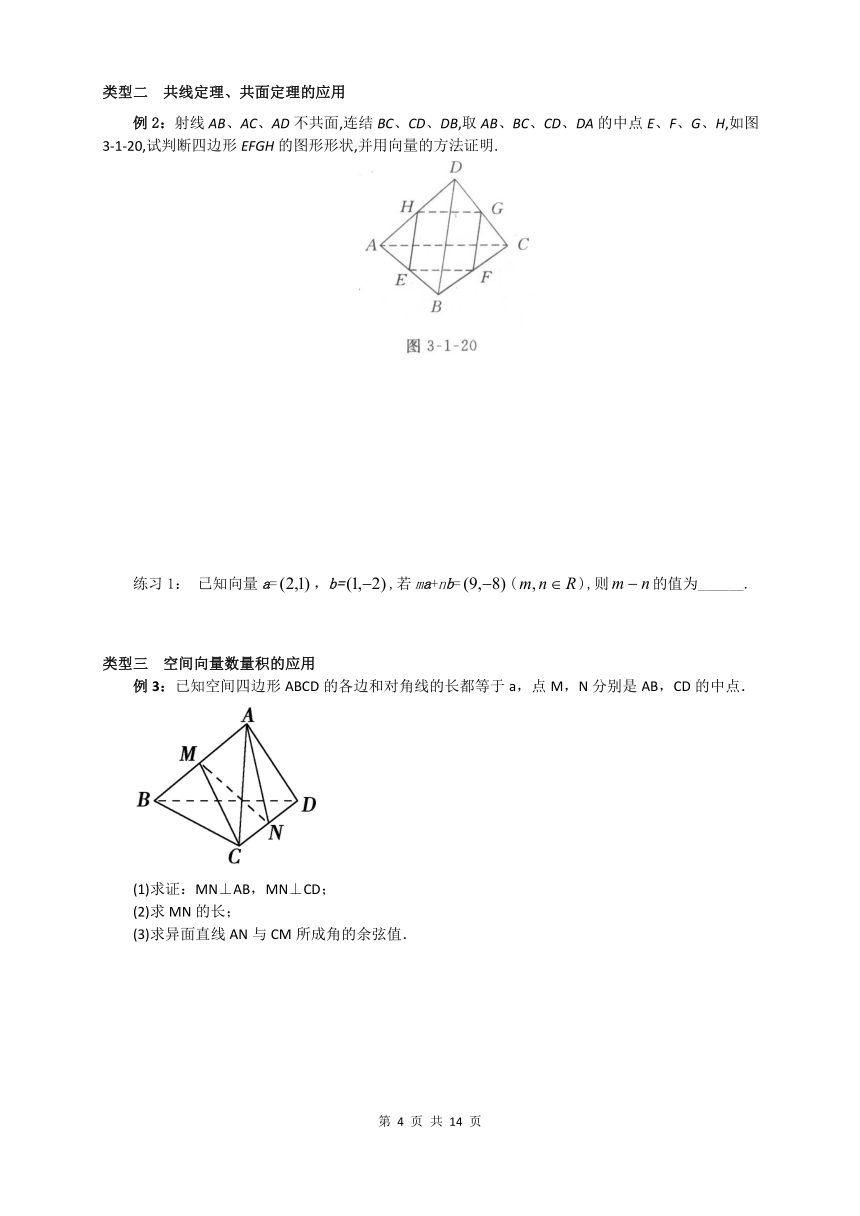
例2:射线AB、AC、AD不共面,连结BC、CD、DB,取AB、BC、CD、DA的中点E、F、G、H,如图3-1-20,试判断四边形EFGH的图形形状,并用向量的方法证明.
练习1: 已知向量a=,b=,若ma+nb=(),则的值为______.
类型三 空间向量数量积的应用
例3:已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
练习1:在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
求1与夹角的余弦值.
1. 已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
2.在下列命题中:
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量a,b,c,则对于空间的任意一个向量p总存在实数x,y,z使得p=xa+yb+zc.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
3.在空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是( )
A.垂直 B.平行
C.异面 D.相交但不垂直
4.O为空间任意一点,若=++,则A,B,C,P四点( )
A.一定不共面 B.一定共面
C.不一定共面 D.无法判断
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1.已知a=(-2,1,3),b=(-1,2,1),若a⊥(a-λb),则实数λ的值为( )
A.-2 B.- C. D.2
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2 C.a2 D.a2
3.若向量c垂直于不共线的向量a和b,d=λa+μb(λ,μ∈R,且λμ≠0),则( )
A.c∥d
B.c⊥d
C.c不平行于d,c也不垂直于d
D.以上三种情况均有可能
4.已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,一向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
5.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则以b,c为方向向量的两直线的夹角为________.
6.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ等于________.
能力提升(2)
7.在四面体OABC中,=a,=b,=c,D为BC的中点,E为AD的中点,则=________(用a,b,c表示).
8.A,B,C,D是空间不共面四点,且·=0,·=0,·=0,则△BCD的形状是________三角形(填锐角、直角、钝角中的一个).
9.已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若|c|=3,且c∥,求向量c.
(2)求向量a与向量b的夹角的余弦值.
参考答案
类型一 空间向量的线性运算
例1:如图3-1-6,已知平行六面体.
求证:
【解析】:由于在平行六面体中,每个面都是平行四边形,故可结合空间向量加法的平行四边形法则进行向量的运算,从而证明结论.
【答案】∵平行六面体的六个面均为平行四边形,
∴
又∵
练习1:如图所示,在平行六面体ABCD-A1B1C1D1中,设1=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:,
【答案】(1)=a+c+;(2)=-a+b+
练习2: 设向量,不平行,向量与平行,则实数_________.
【答案】
类型二 共线定理、共面定理的应用
例2:射线AB、AC、AD不共面,连结BC、CD、DB,取AB、BC、CD、DA的中点E、F、G、H,如图3-1-20,试判断四边形EFGH的图形形状,并用向量的方法证明.
【答案】
解法1:四边形EFGH是平行四边形.
∵
∵E点不在上,∴EH∥FG,且EH=FG,
∴四边形EFGH是平行四边形.
解法2:∵
∴又H点不在上,
∴HG∥EF,且HG=EF.
∴四边形EFGH是平行四边形.
练习1: 已知向量a=,b=,若ma+nb=(),则的值为______.
【解析】由题意得:
【答案】
类型三 空间向量数量积的应用
例3:已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
【解析】(1)设=p,=q,=r.
由题意可知:|p|=|q|=|r|=a,且p、q、r三向量两两夹角均为60°.
=-=(+)-=(q+r-p),
∴·=(q+r-p)·p
=(q·p+r·p-p2)=(a2·cos60°+a2·cos60°-a2)=0.
∴MN⊥AB,同理可证MN⊥CD.
(2)由(1)可知=(q+r-p)
∴||2=2=(q+r-p)2=[q2+r2+p2+2(q·r-p·q-r·p)]
=[a2+a2+a2+2(--)=×2a2=.
∴||=a,∴MN的长为a.
(3)解 设向量与的夹角为θ.
∵=(+)=(q+r),
=-=q-p,
∴·=(q+r)·(q-p)
=(q2-q·p+r·q-r·p)
=(a2-a2cos60°+a2cos60°-a2cos60°)=.
又∵||=||=a,
∴·=||||cosθ=a×a×cosθ=.
∴cosθ=.
∴向量与的夹角的余弦值为,从而异面直线AN与CM所成角的余弦值为.
【答案】(1)见解析(2)MN的长为a.(3)异面直线AN与CM所成角的余弦值为
练习1:在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
求1与夹角的余弦值.
【答案】设=a,=b.=c
=b+c-a,=a+b,
∴||=,||=,
·=(b+c-a)·(a+b)=b2-a2+a·c+b·c=1.
∴cos〈,〉==.
1. 已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
【答案】B
2.在下列命题中:
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量a,b,c,则对于空间的任意一个向量p总存在实数x,y,z使得p=xa+yb+zc.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
【答案】A
3.在空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是( )
A.垂直 B.平行
C.异面 D.相交但不垂直
【答案】B
4.O为空间任意一点,若=++,则A,B,C,P四点( )
A.一定不共面 B.一定共面
C.不一定共面 D.无法判断
【答案】B
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1.已知a=(-2,1,3),b=(-1,2,1),若a⊥(a-λb),则实数λ的值为( )
A.-2 B.- C. D.2
【答案】D
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2 C.a2 D.a2
【答案】C
3.若向量c垂直于不共线的向量a和b,d=λa+μb(λ,μ∈R,且λμ≠0),则( )
A.c∥d
B.c⊥d
C.c不平行于d,c也不垂直于d
D.以上三种情况均有可能
【答案】B
4.已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,一向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
【答案】B
5.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则以b,c为方向向量的两直线的夹角为________.
【答案】60°
6.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ等于________.
【答案】
能力提升(2)
7.在四面体OABC中,=a,=b,=c,D为BC的中点,E为AD的中点,则=________(用a,b,c表示).
【答案】
8.A,B,C,D是空间不共面四点,且·=0,·=0,·=0,则△BCD的形状是________三角形(填锐角、直角、钝角中的一个).
【答案】锐角
9.已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若|c|=3,且c∥,求向量c.
(2)求向量a与向量b的夹角的余弦值.
【答案】解 (1)∵c∥,=(-3,0,4)-(-1,1,2)=(-2,-1,2),
∴c=m=m(-2,-1,2)=(-2m,-m,2m),
∴|c|==3|m|=3,
∴m=±1.
∴c=(-2,-1,2)或(2,1,-2).
(2)∵a=(1,1,0),b=(-1,0,2),
∴a·b=(1,1,0)·(-1,0,2)=-1,
又∵|a|==,
|b|==,
∴cos〈a,b〉===-,
即向量a与向量b的夹角的余弦值为-.
所以异面直线AG与CE所成角的余弦值为.
(
第
1
页 共
16
页
)
__________________________________________________________________________________
__________________________________________________________________________________
1 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示;
2 掌握空间向量的线性运算及其坐标表示;
3 掌握空间向量的数量积及其坐标表示,能用向量的数量积判断向量的共线和垂直.
1.空间向量的有关概念
名称 概念 表示
零向量 模为0的向量 0
单位向量 长度(模)为1的向量
相等向量 方向相同且模相等的向量 a=b
相反向量 方向相反且模相等的向量 a的相反向量为-a
共线向量 表示空间向量的有向线段所在的直线互相平行或重合 a∥b
共面向量 平行于同一个平面的向量
2.共线向量、共面向量定理和空间向量基本定理
(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使得a=λb.
(2)共面向量定理:若两个向量a,b不共线,则向量p与向量a,b共面?存在唯一的有序实数对(x,y),使p=xa+yb.
(3)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc,把{a,b,c}叫做空间的一个基底.
3.空间向量的数量积及运算律
(1)数量积及相关概念
①两向量的夹角
已知两个非零向量a,b,在空间任取一点O,作=a,=b,则∠AOB叫做向量a与b的夹角,记作〈a,b〉,其范围是0≤〈a,b〉≤π,若〈a,b〉=,则称a与b互相垂直,记作a⊥b.
②两向量的数量积
已知空间两个非零向量a,b,则|a||b|cos〈a,b〉叫做向量a,b的数量积,记作a·b,即a·b=|a||b|cos〈a,b〉.
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
③分配律:a·(b+c)=a·b+a·c.
4.空间向量的坐标表示及其应用
设a=(a1,a2,a3),b=(b1,b2,b3).
向量表示[ 坐标表示
数量积 a·b a1b1+a2b2+a3b3
共线 a=λb(b≠0) a1=λb1,a2=λb2,a3=λb3
垂直 a·b=0 (a≠0,b≠0) a1b1+a2b2+a3b3=0
模 |a|
夹角 〈a,b〉(a≠0,b≠0) cos〈a,b〉=
规律方法:
1.选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决立体几何问题的基本要求.如本例用,,表示,等,另外解题时应结合已知和所求观察图形,联想相关的运算法则和公式等,就近表示所需向量.
(2.首尾相接的若干个向量的和,等于由起始向量的起点指向末尾向量的终点的向量.所以在求若干向量的和,可以通过平移将其转化为首尾相接的向量求和.
3.数量积的应用:
求夹角,设向量a,b所成的角为θ,则cosθ=,进而可求两异面直线所成的角;
(2)求长度(距离),运用公式|a|2=a·a,可使线段长度的计算问题转化为向量数量积的计算问题;(3)解决垂直问题,利用a⊥ba·b=0(a≠0,b≠0),可将垂直问题转化为向量数量积的计算问题.
类型一 空间向量的线性运算
例1:如图3-1-6,已知平行六面体.
求证:
练习1:如图所示,在平行六面体ABCD-A1B1C1D1中,设1=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:,
练习2: 设向量,不平行,向量与平行,则实数_________.
类型二 共线定理、共面定理的应用
例2:射线AB、AC、AD不共面,连结BC、CD、DB,取AB、BC、CD、DA的中点E、F、G、H,如图3-1-20,试判断四边形EFGH的图形形状,并用向量的方法证明.
练习1: 已知向量a=,b=,若ma+nb=(),则的值为______.
类型三 空间向量数量积的应用
例3:已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
练习1:在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
求1与夹角的余弦值.
1. 已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
2.在下列命题中:
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量a,b,c,则对于空间的任意一个向量p总存在实数x,y,z使得p=xa+yb+zc.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
3.在空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是( )
A.垂直 B.平行
C.异面 D.相交但不垂直
4.O为空间任意一点,若=++,则A,B,C,P四点( )
A.一定不共面 B.一定共面
C.不一定共面 D.无法判断
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1.已知a=(-2,1,3),b=(-1,2,1),若a⊥(a-λb),则实数λ的值为( )
A.-2 B.- C. D.2
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2 C.a2 D.a2
3.若向量c垂直于不共线的向量a和b,d=λa+μb(λ,μ∈R,且λμ≠0),则( )
A.c∥d
B.c⊥d
C.c不平行于d,c也不垂直于d
D.以上三种情况均有可能
4.已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,一向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
5.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则以b,c为方向向量的两直线的夹角为________.
6.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ等于________.
能力提升(2)
7.在四面体OABC中,=a,=b,=c,D为BC的中点,E为AD的中点,则=________(用a,b,c表示).
8.A,B,C,D是空间不共面四点,且·=0,·=0,·=0,则△BCD的形状是________三角形(填锐角、直角、钝角中的一个).
9.已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若|c|=3,且c∥,求向量c.
(2)求向量a与向量b的夹角的余弦值.
参考答案
类型一 空间向量的线性运算
例1:如图3-1-6,已知平行六面体.
求证:
【解析】:由于在平行六面体中,每个面都是平行四边形,故可结合空间向量加法的平行四边形法则进行向量的运算,从而证明结论.
【答案】∵平行六面体的六个面均为平行四边形,
∴
又∵
练习1:如图所示,在平行六面体ABCD-A1B1C1D1中,设1=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:,
【答案】(1)=a+c+;(2)=-a+b+
练习2: 设向量,不平行,向量与平行,则实数_________.
【答案】
类型二 共线定理、共面定理的应用
例2:射线AB、AC、AD不共面,连结BC、CD、DB,取AB、BC、CD、DA的中点E、F、G、H,如图3-1-20,试判断四边形EFGH的图形形状,并用向量的方法证明.
【答案】
解法1:四边形EFGH是平行四边形.
∵
∵E点不在上,∴EH∥FG,且EH=FG,
∴四边形EFGH是平行四边形.
解法2:∵
∴又H点不在上,
∴HG∥EF,且HG=EF.
∴四边形EFGH是平行四边形.
练习1: 已知向量a=,b=,若ma+nb=(),则的值为______.
【解析】由题意得:
【答案】
类型三 空间向量数量积的应用
例3:已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
【解析】(1)设=p,=q,=r.
由题意可知:|p|=|q|=|r|=a,且p、q、r三向量两两夹角均为60°.
=-=(+)-=(q+r-p),
∴·=(q+r-p)·p
=(q·p+r·p-p2)=(a2·cos60°+a2·cos60°-a2)=0.
∴MN⊥AB,同理可证MN⊥CD.
(2)由(1)可知=(q+r-p)
∴||2=2=(q+r-p)2=[q2+r2+p2+2(q·r-p·q-r·p)]
=[a2+a2+a2+2(--)=×2a2=.
∴||=a,∴MN的长为a.
(3)解 设向量与的夹角为θ.
∵=(+)=(q+r),
=-=q-p,
∴·=(q+r)·(q-p)
=(q2-q·p+r·q-r·p)
=(a2-a2cos60°+a2cos60°-a2cos60°)=.
又∵||=||=a,
∴·=||||cosθ=a×a×cosθ=.
∴cosθ=.
∴向量与的夹角的余弦值为,从而异面直线AN与CM所成角的余弦值为.
【答案】(1)见解析(2)MN的长为a.(3)异面直线AN与CM所成角的余弦值为
练习1:在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
求1与夹角的余弦值.
【答案】设=a,=b.=c
=b+c-a,=a+b,
∴||=,||=,
·=(b+c-a)·(a+b)=b2-a2+a·c+b·c=1.
∴cos〈,〉==.
1. 已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
【答案】B
2.在下列命题中:
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量a,b,c,则对于空间的任意一个向量p总存在实数x,y,z使得p=xa+yb+zc.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
【答案】A
3.在空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是( )
A.垂直 B.平行
C.异面 D.相交但不垂直
【答案】B
4.O为空间任意一点,若=++,则A,B,C,P四点( )
A.一定不共面 B.一定共面
C.不一定共面 D.无法判断
【答案】B
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1.已知a=(-2,1,3),b=(-1,2,1),若a⊥(a-λb),则实数λ的值为( )
A.-2 B.- C. D.2
【答案】D
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2 C.a2 D.a2
【答案】C
3.若向量c垂直于不共线的向量a和b,d=λa+μb(λ,μ∈R,且λμ≠0),则( )
A.c∥d
B.c⊥d
C.c不平行于d,c也不垂直于d
D.以上三种情况均有可能
【答案】B
4.已知{a,b,c}是空间的一个基底,{a+b,a-b,c}是空间的另一个基底,一向量p在基底{a,b,c}下的坐标为(4,2,3),则向量p在基底{a+b,a-b,c}下的坐标是( )
A.(4,0,3) B.(3,1,3)
C.(1,2,3) D.(2,1,3)
【答案】B
5.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则以b,c为方向向量的两直线的夹角为________.
【答案】60°
6.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ等于________.
【答案】
能力提升(2)
7.在四面体OABC中,=a,=b,=c,D为BC的中点,E为AD的中点,则=________(用a,b,c表示).
【答案】
8.A,B,C,D是空间不共面四点,且·=0,·=0,·=0,则△BCD的形状是________三角形(填锐角、直角、钝角中的一个).
【答案】锐角
9.已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若|c|=3,且c∥,求向量c.
(2)求向量a与向量b的夹角的余弦值.
【答案】解 (1)∵c∥,=(-3,0,4)-(-1,1,2)=(-2,-1,2),
∴c=m=m(-2,-1,2)=(-2m,-m,2m),
∴|c|==3|m|=3,
∴m=±1.
∴c=(-2,-1,2)或(2,1,-2).
(2)∵a=(1,1,0),b=(-1,0,2),
∴a·b=(1,1,0)·(-1,0,2)=-1,
又∵|a|==,
|b|==,
∴cos〈a,b〉===-,
即向量a与向量b的夹角的余弦值为-.
所以异面直线AG与CE所成角的余弦值为.
(
第
1
页 共
16
页
)
