人教版高中数学选修2-1第一章常用逻辑用语 1.1-1.2命题与充要条件(教师版)【个性化辅导含答案】
文档属性
| 名称 | 人教版高中数学选修2-1第一章常用逻辑用语 1.1-1.2命题与充要条件(教师版)【个性化辅导含答案】 |  | |
| 格式 | zip | ||
| 文件大小 | 908.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-10 16:30:08 | ||
图片预览




文档简介
命题与充要条件
__________________________________________________________________________________
__________________________________________________________________________________
1 理解四种命题及其相互关系,会判断四种命题的真假。
2 理解简单的逻辑联结词“或”“且”“非”的含义,能用“或”“且”“非”表述相关的数学内容。
3 会用“全称量词与存在量词”对命题进行否定。
4 理解充分条件、必要条件、充要条件等概念。
5 能够判断给定的两个命题的充要关系,充分条件与必要条件的判断。
1.命题
能判断真假的语句叫做命题.
四种命题表述形式
原命题:若p,则q
逆命题:若q,则p
否命题:若非p,则非q
逆否命题:若非q,则非p
2.全称量词与全称命题
(1)全称量词:短语“所有”在陈述中表示所述事物的全体,在逻辑中通常叫做全称量词.
(2)全称命题:含有全称量词的命题.
(3)全称命题的符号表示
形如“对M中所有x,p(x)”的命题,可用符号简记为“x∈M,p(x)”.
3.存在量词与存在性命题
(1)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词。
(2)存在性命题:含有全称量词的命题.
(3)存在性命题的符号表示
形如“存在集合M中的元素x,q(x)”的命题,用符号简记为x∈M,q(x)。
4.基本逻辑联结词
常用的基本逻辑联结词有“且”、“或”、“非”.
5.命题p∧q,p∨q,非p的真假判断
p q p∧q p∨q 非p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
6.含有一个量词的命题的否定
命题 命题的否定
x∈M,p(x) x∈M,非p(x)
x∈M,p(x) x∈M,非p(x)
7.充分条件、必要条件与充要条件
(1)“若p,则q”形式的命题为真时,记作pq,称p是q的充分条件,q是p的必要条件.
(2)如果既有pq,又有qp,记作pq,则p是q的充要条件,q也是p的充要条件.
p是q的充要条件又常说成q当且仅当p,或p与q等价.
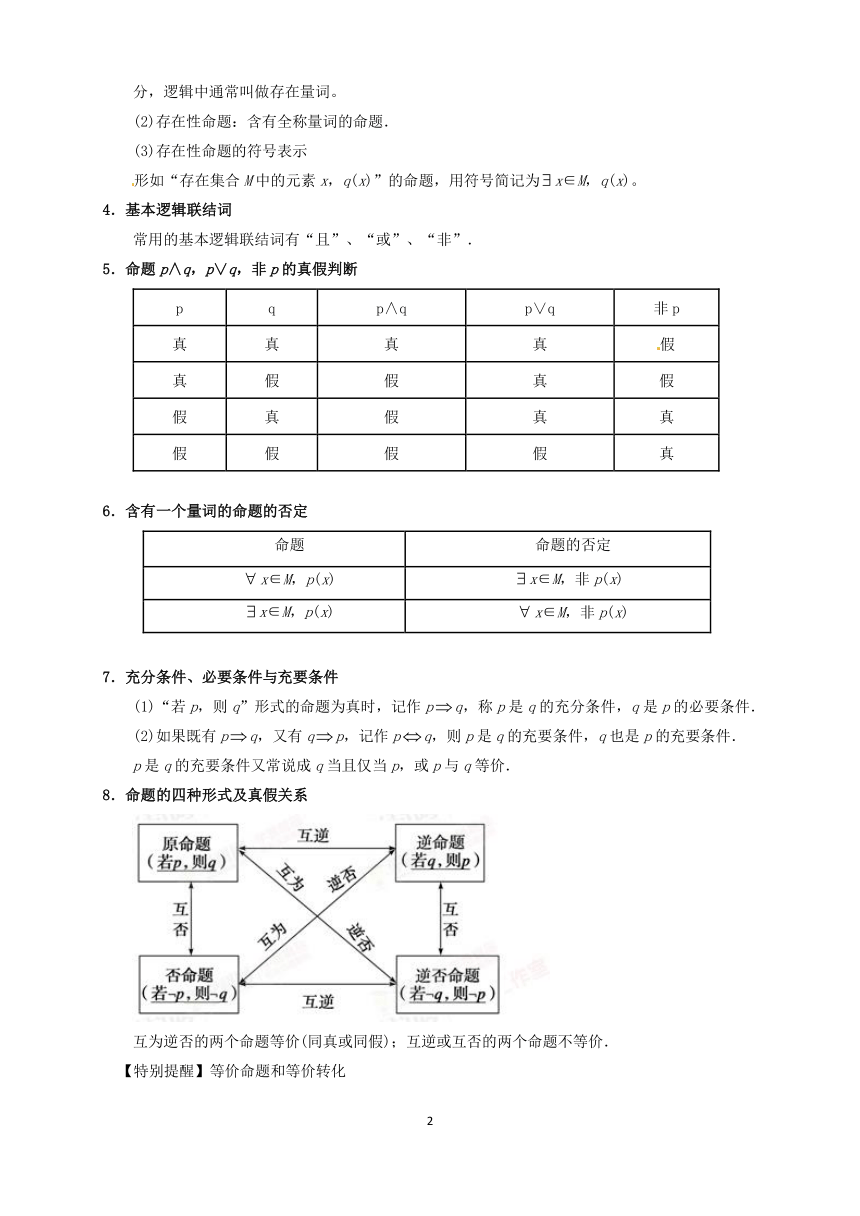
8.命题的四种形式及真假关系
互为逆否的两个命题等价(同真或同假);互逆或互否的两个命题不等价.
【特别提醒】等价命题和等价转化
(1)逆命题与否命题互为逆否命题;
(2)互为逆否命题的两个命题同真假;
(3)当判断原命题的真假比较困难时,可以转化为判断它的逆否命题的真假.
类型一 命题的四种形式及其关系
例1:已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是( )
A.否命题“若函数f(x)=ex-mx在(0,+∞)上是减函数,则m>1”是真命题
B.逆命题“若m≤1,则函数f(x)=ex-mx在(0,+∞)上是增函数”是假命题
C.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上是减函数”是真命题
D.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题
【解析】 命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”是真命题,所以其逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题.
【答案】 D
练习1:给出命题“已知a、b、c、d是实数,若a=b,c=d,则a+c=b+d”,对其原命题、逆命题、否命题、逆否命题而言,真命题有( )
A.0个 B.2个 C.3个 D.4个
【解析】 在四种命题中原命题和逆否命题同真假,故只需判断原命题和逆命题的真假即可.原命题为真.所以逆否命题为真.逆命题为“已知a、b、c、d是实数,若a+c=b+d,则a=b,c=d”,显然错误.所以否命题也错误.故真命题个数为2.
【答案】 B
练习2:命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是( )
A.若x+y是偶数,则x与y不都是偶数
B.若x+y是偶数,则x与y都不是偶数
C.若x+y不是偶数,则x与y不都是偶数
D.若x+y不是偶数,则x与y都不是偶数
【解析】 若命题为“若p则q”,命题的逆否命题为“若非q,则非p”,所以原命题的逆否命题是“若x+y不是偶数,则x与y不都是偶数”。
【答案】 C
类型二 含有逻辑联结词命题真假的判断
例2:设命题p:函数y=sin2x的最小正周期为;命题q:函数y=cosx的图象关于直线x=对称.则下列判断正确的是( )
A.p为真 B.非q为假 C.p∧q为假 D.p∨q为真
【解析】 由于函数y=sin2x的最小正周期为π,故命题P是假命题;函数y=cosx的图象关于直线x=kπ对称,k∈Z,故q是假命题
由此结合复合命题的判断规则知:¬q为真命题,p∧q为假命题,p∨q为是假命题
考查四个选项,C选项正确,
【答案】 C
练习1 :设命题:,则为( )
A. B.
C. D.
【解析】 全称命题的否定与特称命题的否定是高考考查的重点,对特称命题的否定,将存在换成任意,后边变为其否定形式,注意全称命题与特称命题否定的书写,是常规题,很好考查了学生对双基的掌握程度.:,故选C.
【答案】 C
练习2:已知命题p1:函数y=2x-2-x在R上为增函数;p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(非p1)∨p2和q4:p1∧(非p2)中,真命题是( )
A.q1,q3 B.q2,q3 C.q1,q4 D.q2,q4
【解析】 选C.p1为真命题,p2为假命题,∴非p1为假命题,非p2为真命题.故选C.
【答案】 C
例3:判断下列命题的真假.
x∈R,x2-x+1>;
(2)α,β,cos(α-β)=cosα-cosβ;
(3)x,y∈N,x-y∈N;
(4)x0,y0∈Z,x0+y0=3.
【解析】 (1)真命题,x2-x+1=(x-)2+≥>.
(2)真命题,如α=,β=符合题意.
(3)假命题,如x=1,y=5,但x-y=-4N.
(4)真命题,如x0=0,y0=3符合题意.
【答案】 真命题,真命题,假命题,真命题。
练习3:写出下列命题的否定形式,并判断其真假.
(1)p:x∈R,x2-x+≥0;
(2)s:至少存在一个实数x,使x3+1=0.
【解析】 (1)非p:x∈R,x2-x+<0,是假命题,因为x∈R,x2-x+=2≥0恒成立.
非s:x∈R,x3+1≠0,是假命题,因为当x=-1时,x3+1=0.
【答案】 非p:x∈R,x2-x+<0,是假命题。非s:x∈R,x3+1≠0,是假命题。
类型三 充要条件的判断
例4:设集合m={x|x>2},p={x|x<3},那么“x∈m或x∈p”是x∈p∩m的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】“x∈m或x∈p”即x∈R,而x∈p∩m即x∈(2,3).∴x∈p∩mx∈m或x∈p,但x∈m或x∈p推不出x∈p∩m.
【答案】B
练习1:给出下列命题:
①“数列{an}为等比数列”是“数列{anan+1}为等比数列”的充分不必要条件;
② “a=2”是“函数f(x)=|x-a|在区间[2,+∞)上为增函数”的充要条件;
③“m=3”是“直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直”的充要条件;
④设a,b,c分别是△ABC三个内角A,B,C所对的边,若a=1,b=,则“A=30°”是“B=60°”的必要不充分条件.
其中真命题的序号是________.
【解析】 对于①,当数列{an}是等比数列时,易知数列{anan+1}是等比数列;但当数列{anan+1}是等比数列时,数列{an}未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确.对于②,当a≤2时,函数f(x)=|x-a|在区间[2,+∞)上是增函数,因此②不正确.对于③,当m=3时,相应的两条直线垂直;反过来,当这两条直线垂直时,不一定能得出m=3,也可能得出m=0,因此③不正确.对于④,由题意,得=,当B=60°时,有sinA=,注意到b>a,故A=30°;但当A=30°时,有sinB=,B=60°或B=120°,因此④正确.
【答案】 ①④
练习2 :设,.若p:成等比数列;
q:,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
【解析】 充分性:若命题p成立,不妨设数列的公比为,则根据柯西不等式,当,时,命题q成立,因此充分性成立;
必要性:当时,命题q成立,而不为等比数列,即命题p不成立,故必要性不成立。
综上,p是q的充分条件,但不是q的必要条件。
故本题正确答案为A
【答案】 A
类型三 求参数的取值范围
例5:已知p:x2-8x-20≤0,q:x2-2x+1-m2≤0(m>0).若非p是非q的充分不必要条件,求实数m的取值范围.
【解析】方法1:由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0得1-m≤x≤1+m(m>0).
∴非p:A={x|x>10或x<-2},非q:B={x|x>1+m或x<1-m}.
∵非p是非q的充分不必要条件,∴AB.
∴解得0方法2:由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0得1-m≤x≤1+m(m>0),
∴p:A={x|-2≤x≤10},q:B={x|1-m≤x≤1+m}.
∵非p是非q的充分不必要条件,∴q也是p的充分不必要条件,∴BA.
∴解得0【答案】0练习1:已知命题p:函数log0.5(x2+2x+a)的值域为R,命题q:函数y=-(5-2a)x是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
A.a≤1 B.a<2 C.1【解析】 分别求命题P为真命题的a的范围,命题q为真命题的a的范围;根据p或q为真命题,p且q为假命题,得到命题p,q中有一个真命题,一个假命题,分命题p为真命题且命题q为假命题和命题q为真命题且命题p为假命题两类求出a的范围.本题考查根据复合命题的真假得到构成其简单命题的真假情况.解:命题p为真时,即真数部分能够取到大于零的所有实数,故二次函数x2+2x+a的判别式△=4-4a≥0,从而a≤1;命题q为真时,5-2a>1?a<2.若p或q为真命题,p且q为假命题,故p和q中只有一个是真命题,一个是假命题.若p为真,q为假时,无解;若p为假,q为真时,结果为1<a<2。
【答案】 C.
练习2:已知c>0,且c≠1,设p:函数y=cx在R上递减;q:函数f(x)=x2-2cx-1在上为增函数,若“p且q”为假,“p或q”为真,则实数c的取值范围为________.
【解析】 若p为真,∵函数y=cx在R上单调递减,∴0<c<1,若q为真,∵函数f(x)=x2-2cx+1在(1/2,+∞)上为增函数f(x)对称轴为x=c,∴0<c≤1/2
(1)p为真,q为假,∴实数c的取值范围是1/2(2)p假q真,无解。
∴实数c的取值范围是1/2【答案】 1/2类型四 充要条件的应用
例6:已知集合M={x||x+1|+|x-3|>8},P={x|x2+(a-8)x-8a≤0},若M∩P={x|5<x≤8}求a取值范围。
【解析】 解M:当x>3时x+1+x-3>8,得x>5。当-18,无解。当x≤-1时,-x-1+3-x>8,得x<-3。即M={x|x>5或x<-3},M∩P={x|5<x≤8},则 记f(x)=x2+(a-8)x-8a=0两根x1【答案】 解M:当x>3时x+1+x-3>8,得x>5。当-18,无解。当x≤-1时,-x-1+3-x>8,得x<-3。即M={x|x>5 or x<-3},M∩P={x|5<x≤8},则 记f(x)=x2+(a-8)x-8a=0两根x1练习1:已知p:x2-4x-5≤0,q:|x-3|0).若p是q的充分不必要条件,求a的取值范围.
【解析】 设A={x|x2-4x-5≤0}={x|-1≤x≤5},B={x|-a+34。
【答案】 设A={x|x2-4x-5≤0}={x|-1≤x≤5},B={x|-a+34。
1.已知命题p:函数f(x)=-在区间内存在零点,命题q:存在负数x使得
>给出下列四个命题:①p或q;②p且q;③p的否定;④q的否定.其中真命题的个数是( )
A.1 B.2 C.3 D.4
【解析】命题p为假命题,命题q也为假命题.利用真值表判断.
【答案】B
2.命题“若α=,则tanα=1”的逆否命题是( )
A.若α≠,则tanα≠1 B.若α=,则tanα≠1
C.若tanα≠1,则α≠ D.若tanα≠1,则α=
【答案】 C
3. 设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】 A
4.下列命题中为真命题的是( )
A.命题“若x>y,则x>|y|”的逆命题
B.命题“若x>1,则x2>1”的否命题
C.命题“若x=1,则x2+x-2=0”的否命题
D.命题“若x2>0,则x>1”的逆否命题
【答案】 A
5.已知p(x):x2+2x-m>0,如果p(1)是假命题,p(2)是真命题,则实数m的取值范围为________.
【答案】 [3,8)
6.已知p:|x-3|≤2,q:(x-m+1)(x-m-1)≤0,若非p是非q的充分而不必要条件,求实数m的取值范围.
【答案】 由题意得p:-2≤x-3≤2,∴1≤x≤5.
∴非p:x<1或x>5.
q:m-1≤x≤m+1,∴非q:xm+1.
又∵非p是非q的充分而不必要条件,
∴或,
解得2
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1. 设命题:,则为( )
A. B.
C. D.
【答案】 C
2. 命题“且的否定形式是( )
A.且 B.或
C.且 D.或
【答案】 D.
3.判断命题“若a≥0,则x2+x-a=0有实根”的逆否命题的真假.
【答案】 逆否命题:若x2+x-a=0无实根,则a<0.
判断如下:
∵x2+x-a=0无实根,∴Δ=1+4a<0,∴a<-<0,
∴“若x2+x-a=0无实根,则a<0”为真命题.
4.下列命题:
①若ac2>bc2,则a>b;
②若sinα=sinβ,则α=β;
③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;
④若f(x)=log2x,则f(|x|)是偶函数.
其中正确命题的序号是________.
【答案】 ①③④
设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n=________.
【答案】 3或4
能力提升(2)
6.若“x∈[2,5]或x∈{x|x<1或x>4}”是假命题,则x的取值范围是________.
【答案】 [1,2)
“m<”是“一元二次方程x2+x+m=0有实数解”的____________条件.
【答案】 充分不必要
设有两个命题p、q.其中p:对于任意的x∈R,不等式ax2+2x+1>0恒成立;命题q:f(x)=(4a-3)x在R上为减函.如果两个命题中有且只有一个是真命题,那么实数a的取值范围是____________.
【答案】 ∪(1,+∞)
9.求证:一元二次方程ax2+bx+c=0(a≠0)的两根都大于3是的一个充分不必要条件.
【答案】证明:先证充分性:由于方程的两根都大于3,即x1>3,x2>3,可得成立;再证不必要性:
若成立,不一定推出两根都大于3.如:x1=1,x2=10时x1+x2>6,x1x2>9,但x1>3不成立,从而原命题得证.
9
__________________________________________________________________________________
__________________________________________________________________________________
1 理解四种命题及其相互关系,会判断四种命题的真假。
2 理解简单的逻辑联结词“或”“且”“非”的含义,能用“或”“且”“非”表述相关的数学内容。
3 会用“全称量词与存在量词”对命题进行否定。
4 理解充分条件、必要条件、充要条件等概念。
5 能够判断给定的两个命题的充要关系,充分条件与必要条件的判断。
1.命题
能判断真假的语句叫做命题.
四种命题表述形式
原命题:若p,则q
逆命题:若q,则p
否命题:若非p,则非q
逆否命题:若非q,则非p
2.全称量词与全称命题
(1)全称量词:短语“所有”在陈述中表示所述事物的全体,在逻辑中通常叫做全称量词.
(2)全称命题:含有全称量词的命题.
(3)全称命题的符号表示
形如“对M中所有x,p(x)”的命题,可用符号简记为“x∈M,p(x)”.
3.存在量词与存在性命题
(1)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词。
(2)存在性命题:含有全称量词的命题.
(3)存在性命题的符号表示
形如“存在集合M中的元素x,q(x)”的命题,用符号简记为x∈M,q(x)。
4.基本逻辑联结词
常用的基本逻辑联结词有“且”、“或”、“非”.
5.命题p∧q,p∨q,非p的真假判断
p q p∧q p∨q 非p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
6.含有一个量词的命题的否定
命题 命题的否定
x∈M,p(x) x∈M,非p(x)
x∈M,p(x) x∈M,非p(x)
7.充分条件、必要条件与充要条件
(1)“若p,则q”形式的命题为真时,记作pq,称p是q的充分条件,q是p的必要条件.
(2)如果既有pq,又有qp,记作pq,则p是q的充要条件,q也是p的充要条件.
p是q的充要条件又常说成q当且仅当p,或p与q等价.
8.命题的四种形式及真假关系
互为逆否的两个命题等价(同真或同假);互逆或互否的两个命题不等价.
【特别提醒】等价命题和等价转化
(1)逆命题与否命题互为逆否命题;
(2)互为逆否命题的两个命题同真假;
(3)当判断原命题的真假比较困难时,可以转化为判断它的逆否命题的真假.
类型一 命题的四种形式及其关系
例1:已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是( )
A.否命题“若函数f(x)=ex-mx在(0,+∞)上是减函数,则m>1”是真命题
B.逆命题“若m≤1,则函数f(x)=ex-mx在(0,+∞)上是增函数”是假命题
C.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上是减函数”是真命题
D.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题
【解析】 命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”是真命题,所以其逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题.
【答案】 D
练习1:给出命题“已知a、b、c、d是实数,若a=b,c=d,则a+c=b+d”,对其原命题、逆命题、否命题、逆否命题而言,真命题有( )
A.0个 B.2个 C.3个 D.4个
【解析】 在四种命题中原命题和逆否命题同真假,故只需判断原命题和逆命题的真假即可.原命题为真.所以逆否命题为真.逆命题为“已知a、b、c、d是实数,若a+c=b+d,则a=b,c=d”,显然错误.所以否命题也错误.故真命题个数为2.
【答案】 B
练习2:命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是( )
A.若x+y是偶数,则x与y不都是偶数
B.若x+y是偶数,则x与y都不是偶数
C.若x+y不是偶数,则x与y不都是偶数
D.若x+y不是偶数,则x与y都不是偶数
【解析】 若命题为“若p则q”,命题的逆否命题为“若非q,则非p”,所以原命题的逆否命题是“若x+y不是偶数,则x与y不都是偶数”。
【答案】 C
类型二 含有逻辑联结词命题真假的判断
例2:设命题p:函数y=sin2x的最小正周期为;命题q:函数y=cosx的图象关于直线x=对称.则下列判断正确的是( )
A.p为真 B.非q为假 C.p∧q为假 D.p∨q为真
【解析】 由于函数y=sin2x的最小正周期为π,故命题P是假命题;函数y=cosx的图象关于直线x=kπ对称,k∈Z,故q是假命题
由此结合复合命题的判断规则知:¬q为真命题,p∧q为假命题,p∨q为是假命题
考查四个选项,C选项正确,
【答案】 C
练习1 :设命题:,则为( )
A. B.
C. D.
【解析】 全称命题的否定与特称命题的否定是高考考查的重点,对特称命题的否定,将存在换成任意,后边变为其否定形式,注意全称命题与特称命题否定的书写,是常规题,很好考查了学生对双基的掌握程度.:,故选C.
【答案】 C
练习2:已知命题p1:函数y=2x-2-x在R上为增函数;p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(非p1)∨p2和q4:p1∧(非p2)中,真命题是( )
A.q1,q3 B.q2,q3 C.q1,q4 D.q2,q4
【解析】 选C.p1为真命题,p2为假命题,∴非p1为假命题,非p2为真命题.故选C.
【答案】 C
例3:判断下列命题的真假.
x∈R,x2-x+1>;
(2)α,β,cos(α-β)=cosα-cosβ;
(3)x,y∈N,x-y∈N;
(4)x0,y0∈Z,x0+y0=3.
【解析】 (1)真命题,x2-x+1=(x-)2+≥>.
(2)真命题,如α=,β=符合题意.
(3)假命题,如x=1,y=5,但x-y=-4N.
(4)真命题,如x0=0,y0=3符合题意.
【答案】 真命题,真命题,假命题,真命题。
练习3:写出下列命题的否定形式,并判断其真假.
(1)p:x∈R,x2-x+≥0;
(2)s:至少存在一个实数x,使x3+1=0.
【解析】 (1)非p:x∈R,x2-x+<0,是假命题,因为x∈R,x2-x+=2≥0恒成立.
非s:x∈R,x3+1≠0,是假命题,因为当x=-1时,x3+1=0.
【答案】 非p:x∈R,x2-x+<0,是假命题。非s:x∈R,x3+1≠0,是假命题。
类型三 充要条件的判断
例4:设集合m={x|x>2},p={x|x<3},那么“x∈m或x∈p”是x∈p∩m的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】“x∈m或x∈p”即x∈R,而x∈p∩m即x∈(2,3).∴x∈p∩mx∈m或x∈p,但x∈m或x∈p推不出x∈p∩m.
【答案】B
练习1:给出下列命题:
①“数列{an}为等比数列”是“数列{anan+1}为等比数列”的充分不必要条件;
② “a=2”是“函数f(x)=|x-a|在区间[2,+∞)上为增函数”的充要条件;
③“m=3”是“直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直”的充要条件;
④设a,b,c分别是△ABC三个内角A,B,C所对的边,若a=1,b=,则“A=30°”是“B=60°”的必要不充分条件.
其中真命题的序号是________.
【解析】 对于①,当数列{an}是等比数列时,易知数列{anan+1}是等比数列;但当数列{anan+1}是等比数列时,数列{an}未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确.对于②,当a≤2时,函数f(x)=|x-a|在区间[2,+∞)上是增函数,因此②不正确.对于③,当m=3时,相应的两条直线垂直;反过来,当这两条直线垂直时,不一定能得出m=3,也可能得出m=0,因此③不正确.对于④,由题意,得=,当B=60°时,有sinA=,注意到b>a,故A=30°;但当A=30°时,有sinB=,B=60°或B=120°,因此④正确.
【答案】 ①④
练习2 :设,.若p:成等比数列;
q:,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
【解析】 充分性:若命题p成立,不妨设数列的公比为,则根据柯西不等式,当,时,命题q成立,因此充分性成立;
必要性:当时,命题q成立,而不为等比数列,即命题p不成立,故必要性不成立。
综上,p是q的充分条件,但不是q的必要条件。
故本题正确答案为A
【答案】 A
类型三 求参数的取值范围
例5:已知p:x2-8x-20≤0,q:x2-2x+1-m2≤0(m>0).若非p是非q的充分不必要条件,求实数m的取值范围.
【解析】方法1:由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0得1-m≤x≤1+m(m>0).
∴非p:A={x|x>10或x<-2},非q:B={x|x>1+m或x<1-m}.
∵非p是非q的充分不必要条件,∴AB.
∴解得0
∴p:A={x|-2≤x≤10},q:B={x|1-m≤x≤1+m}.
∵非p是非q的充分不必要条件,∴q也是p的充分不必要条件,∴BA.
∴解得0
A.a≤1 B.a<2 C.1
【答案】 C.
练习2:已知c>0,且c≠1,设p:函数y=cx在R上递减;q:函数f(x)=x2-2cx-1在上为增函数,若“p且q”为假,“p或q”为真,则实数c的取值范围为________.
【解析】 若p为真,∵函数y=cx在R上单调递减,∴0<c<1,若q为真,∵函数f(x)=x2-2cx+1在(1/2,+∞)上为增函数f(x)对称轴为x=c,∴0<c≤1/2
(1)p为真,q为假,∴实数c的取值范围是1/2
∴实数c的取值范围是1/2
例6:已知集合M={x||x+1|+|x-3|>8},P={x|x2+(a-8)x-8a≤0},若M∩P={x|5<x≤8}求a取值范围。
【解析】 解M:当x>3时x+1+x-3>8,得x>5。当-1
【解析】 设A={x|x2-4x-5≤0}={x|-1≤x≤5},B={x|-a+3
【答案】 设A={x|x2-4x-5≤0}={x|-1≤x≤5},B={x|-a+3
1.已知命题p:函数f(x)=-在区间内存在零点,命题q:存在负数x使得
>给出下列四个命题:①p或q;②p且q;③p的否定;④q的否定.其中真命题的个数是( )
A.1 B.2 C.3 D.4
【解析】命题p为假命题,命题q也为假命题.利用真值表判断.
【答案】B
2.命题“若α=,则tanα=1”的逆否命题是( )
A.若α≠,则tanα≠1 B.若α=,则tanα≠1
C.若tanα≠1,则α≠ D.若tanα≠1,则α=
【答案】 C
3. 设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】 A
4.下列命题中为真命题的是( )
A.命题“若x>y,则x>|y|”的逆命题
B.命题“若x>1,则x2>1”的否命题
C.命题“若x=1,则x2+x-2=0”的否命题
D.命题“若x2>0,则x>1”的逆否命题
【答案】 A
5.已知p(x):x2+2x-m>0,如果p(1)是假命题,p(2)是真命题,则实数m的取值范围为________.
【答案】 [3,8)
6.已知p:|x-3|≤2,q:(x-m+1)(x-m-1)≤0,若非p是非q的充分而不必要条件,求实数m的取值范围.
【答案】 由题意得p:-2≤x-3≤2,∴1≤x≤5.
∴非p:x<1或x>5.
q:m-1≤x≤m+1,∴非q:x
又∵非p是非q的充分而不必要条件,
∴或,
解得2
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固(1)
1. 设命题:,则为( )
A. B.
C. D.
【答案】 C
2. 命题“且的否定形式是( )
A.且 B.或
C.且 D.或
【答案】 D.
3.判断命题“若a≥0,则x2+x-a=0有实根”的逆否命题的真假.
【答案】 逆否命题:若x2+x-a=0无实根,则a<0.
判断如下:
∵x2+x-a=0无实根,∴Δ=1+4a<0,∴a<-<0,
∴“若x2+x-a=0无实根,则a<0”为真命题.
4.下列命题:
①若ac2>bc2,则a>b;
②若sinα=sinβ,则α=β;
③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;
④若f(x)=log2x,则f(|x|)是偶函数.
其中正确命题的序号是________.
【答案】 ①③④
设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n=________.
【答案】 3或4
能力提升(2)
6.若“x∈[2,5]或x∈{x|x<1或x>4}”是假命题,则x的取值范围是________.
【答案】 [1,2)
“m<”是“一元二次方程x2+x+m=0有实数解”的____________条件.
【答案】 充分不必要
设有两个命题p、q.其中p:对于任意的x∈R,不等式ax2+2x+1>0恒成立;命题q:f(x)=(4a-3)x在R上为减函.如果两个命题中有且只有一个是真命题,那么实数a的取值范围是____________.
【答案】 ∪(1,+∞)
9.求证:一元二次方程ax2+bx+c=0(a≠0)的两根都大于3是的一个充分不必要条件.
【答案】证明:先证充分性:由于方程的两根都大于3,即x1>3,x2>3,可得成立;再证不必要性:
若成立,不一定推出两根都大于3.如:x1=1,x2=10时x1+x2>6,x1x2>9,但x1>3不成立,从而原命题得证.
9
