一 《周髀算经》与赵爽弦图 课件(21张PPT)
文档属性
| 名称 | 一 《周髀算经》与赵爽弦图 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 11:39:10 | ||
图片预览







文档简介
课件21张PPT。《周髀算经》与赵爽弦图 李淳风在数学方面的主要贡献,是编定和注释著名的十部算经。《周髀》是其中的第一部。这十部算经后被用作唐代国子监算学馆的数学教材,故改名《周髀算经》。 左边这幅图叫“弦图”,为赵爽所作,后世人将这幅“弦图”称为“赵爽弦图”。
《周髀算经》是中国最古老的天文学和数学著作,成书年代应不晚于公元前1世纪。与数学有关的内容是:学习数学的方法,用勾股定理测量、计算深高远,近似分数计算等等。其中关于勾股定理的论述最为突出。 昔者周公问于商高曰:“窃闻乎大夫善数也,请问昔者包牺立周天历度—夫天可不阶而升,地不可得尺寸而度,请问数安从出?”
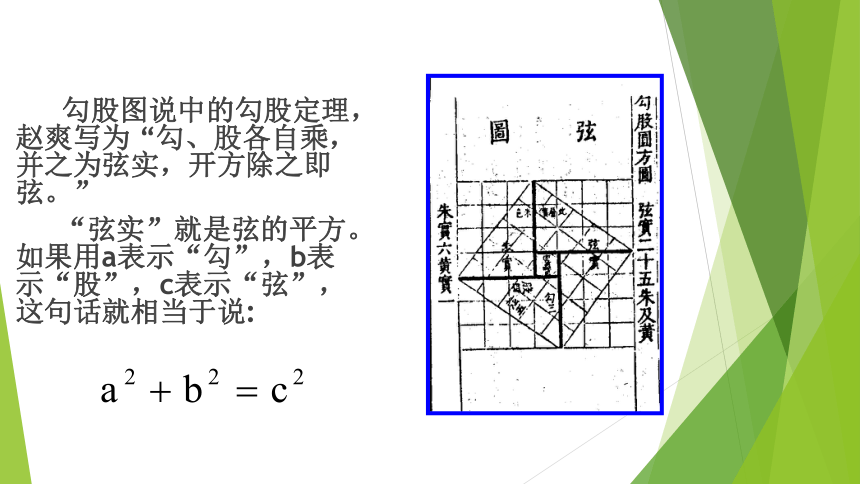
商高曰:“数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。故折矩,以为句广三,股修四,径隅五。既方之,外半其一矩,环而共盘,得成三四五。两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所生也。” 商高答周公 “什么是“勾、股”呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。 我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 发现勾股定理的具体年代已不可详考,但它是在《周髀算经》成书之前发现的是毋庸置疑的事实。 现传的《周髀算经》卷首写有“赵君卿注”。赵君卿名“爽”,即赵爽,三国时期吴国人,他深入研究了《周髀算经》,撰写的“勾股圆方图”说,附录于该书首章的注文中。仅530多字,附图6副,却简练、严密、明确地给出了勾股定理的理论证明。 勾股图说中的勾股定理,赵爽写为 “勾、股各自乘,并之为弦实,开方除之即弦。”
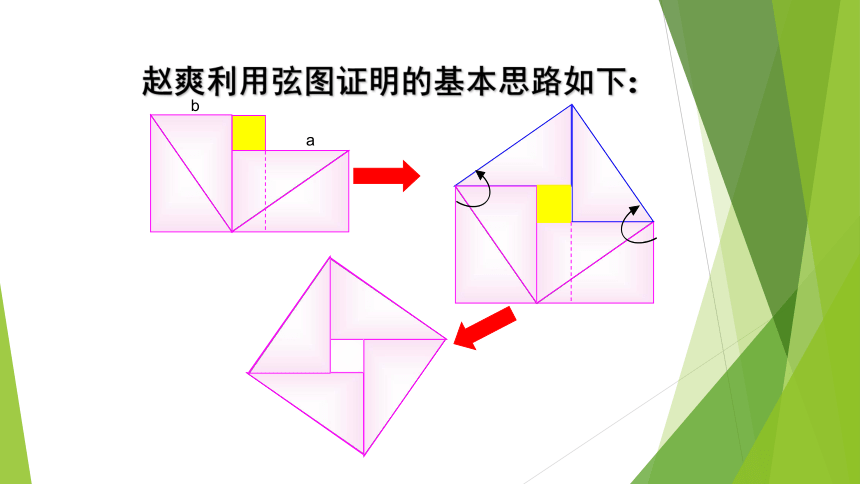
“弦实”就是弦的平方。如果用a表示“勾”,b表示“股”,c表示“弦”,这句话就相当于说:赵爽利用弦图证明的基本思路如下:DEA c2 =a2+b2这就证明了化简得: c2 =a2+ b2. 赵爽成为中国数学史上最早给出勾股定理理论证明的数学家。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,非常直观,为中国古代以形证数、形数统一、代数和几何紧密结合树立了一个典范。以后的数学家大多继承了这一风格并有进一步发展。例如稍后一点的数学家刘徽在证明勾股定理时也是用的以形证数的方法,只是具体图形的分合移补略有不同而已。后人称该图为
“青朱入出图” 刘徽,三国魏晋时代人。他证明勾股定理的过程如图所示:? c2 = b2 + a2印度婆什迦罗的证明 ? c2 = b2 + a2 赵爽,刘徽,婆什伽罗,他们证法的基本思想是:图形经过分割后,面积不变。这就是中国古代数学中重要的的面积“出入相补”原理,是我国古代数学的特色之一。 在西方,最早证明勾股定理的是欧几里得,在他的数学著作《几何原本》有详细的证明过程。欧几里得证明:如图,过点A作ED的垂线,交CB于K,交ED于L.连接AD、CF。??????LK 东方
赵爽追求:直观、适用 西方
欧几里得追求:数学推理出入相补、寓理于算严谨的逻辑与理性的推理整体与直觉思维分析与逻辑思维要兼容两家之长,优势互补作业:1.思考 “青朱入出图”中“朱出”与“朱入”,“青出”与“青入”的面积为什么相等?2.查阅与《周髀算经》有关的书籍或资料,请就里面某一个具体的算例谈谈你的认识,并写出文章。 再 见
《周髀算经》是中国最古老的天文学和数学著作,成书年代应不晚于公元前1世纪。与数学有关的内容是:学习数学的方法,用勾股定理测量、计算深高远,近似分数计算等等。其中关于勾股定理的论述最为突出。 昔者周公问于商高曰:“窃闻乎大夫善数也,请问昔者包牺立周天历度—夫天可不阶而升,地不可得尺寸而度,请问数安从出?”
商高曰:“数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。故折矩,以为句广三,股修四,径隅五。既方之,外半其一矩,环而共盘,得成三四五。两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所生也。” 商高答周公 “什么是“勾、股”呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。 我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 发现勾股定理的具体年代已不可详考,但它是在《周髀算经》成书之前发现的是毋庸置疑的事实。 现传的《周髀算经》卷首写有“赵君卿注”。赵君卿名“爽”,即赵爽,三国时期吴国人,他深入研究了《周髀算经》,撰写的“勾股圆方图”说,附录于该书首章的注文中。仅530多字,附图6副,却简练、严密、明确地给出了勾股定理的理论证明。 勾股图说中的勾股定理,赵爽写为 “勾、股各自乘,并之为弦实,开方除之即弦。”
“弦实”就是弦的平方。如果用a表示“勾”,b表示“股”,c表示“弦”,这句话就相当于说:赵爽利用弦图证明的基本思路如下:DEA c2 =a2+b2这就证明了化简得: c2 =a2+ b2. 赵爽成为中国数学史上最早给出勾股定理理论证明的数学家。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,非常直观,为中国古代以形证数、形数统一、代数和几何紧密结合树立了一个典范。以后的数学家大多继承了这一风格并有进一步发展。例如稍后一点的数学家刘徽在证明勾股定理时也是用的以形证数的方法,只是具体图形的分合移补略有不同而已。后人称该图为
“青朱入出图” 刘徽,三国魏晋时代人。他证明勾股定理的过程如图所示:? c2 = b2 + a2印度婆什迦罗的证明 ? c2 = b2 + a2 赵爽,刘徽,婆什伽罗,他们证法的基本思想是:图形经过分割后,面积不变。这就是中国古代数学中重要的的面积“出入相补”原理,是我国古代数学的特色之一。 在西方,最早证明勾股定理的是欧几里得,在他的数学著作《几何原本》有详细的证明过程。欧几里得证明:如图,过点A作ED的垂线,交CB于K,交ED于L.连接AD、CF。??????LK 东方
赵爽追求:直观、适用 西方
欧几里得追求:数学推理出入相补、寓理于算严谨的逻辑与理性的推理整体与直觉思维分析与逻辑思维要兼容两家之长,优势互补作业:1.思考 “青朱入出图”中“朱出”与“朱入”,“青出”与“青入”的面积为什么相等?2.查阅与《周髀算经》有关的书籍或资料,请就里面某一个具体的算例谈谈你的认识,并写出文章。 再 见
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
