《统计案例》章节小结归纳整合 课件(38张PPT)
文档属性
| 名称 | 《统计案例》章节小结归纳整合 课件(38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 740.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 11:51:31 | ||
图片预览










文档简介
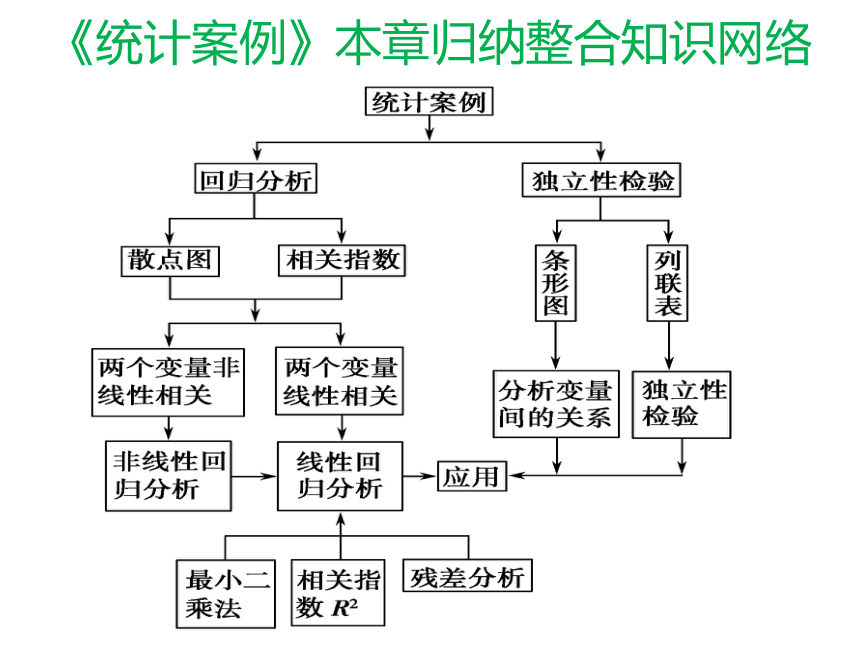
课件38张PPT。永州市一中高中数学选修2-3《统计案例》小结《统计案例》本章归纳整合知识网络例题讲解1、求回归直线方程的方法与技巧例1(安徽卷)某地最近十年粮食需求量逐年上升,下表是部分统计数据:(1)利用所给数据求年需求量与年份之间的回归直线方程 ;(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量.
解:(1)设年份x,需求量y( 万吨):代入所求回归直线方程中:练习1 .在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)作出散点图,你能从散点图中发现投入量x与产量y的一般规律吗?(2)求回归直线方程.(3)预测当投入量x=14时,产量y是多少?
0 1 2 3 解:(1)作出散点图如右图所示:
投入量x与产量y是线性正相关,
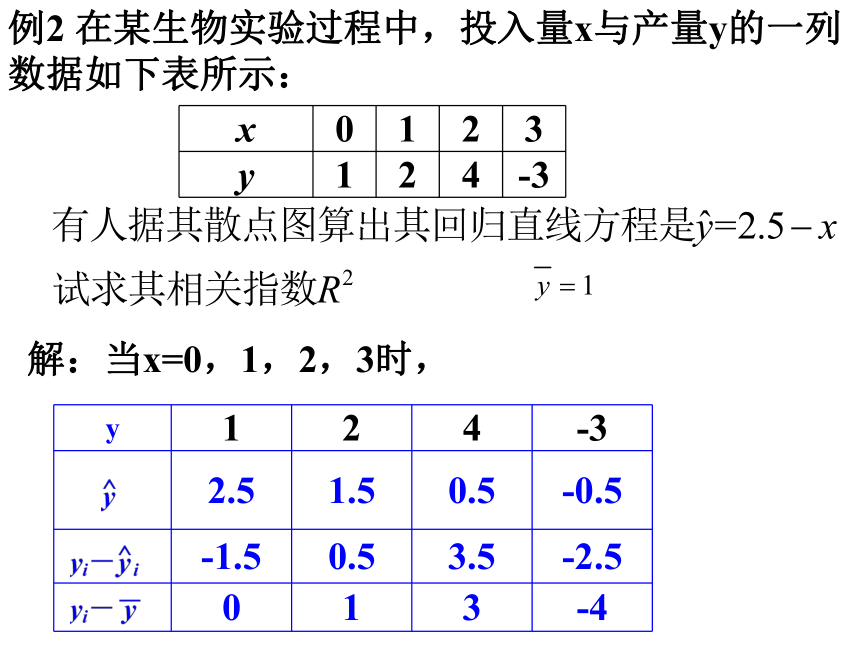
随着投入量x产量y逐渐增加。(2)从图中可以看出,各点散布在一条直线附近,即它们线性相关.(3)预测当产量x=14时,所需的投入量x是20.5.2、相关指数的计算例2 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
解:当x=0,1,2,3时, 解:当x=0,1,2,3时,0 1 2 3 相关指数越大,越接近于1,,模拟的拟合效果越好;相关指数越小,拟合的效果越差!3、回归方程的模型1.直线方程模型;
2.指数函数模型;
3.二次函数模型;
4.反比例函数模型;
5.对数函数模型.1.直线方程模型.2.指数函数模型.3.二次函数模型.4.反比例函数模型.5.对数函数模型. 例3 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.解:(1)作出散点图如右图所示:(2)y与x之间的回归方程是: 4.独立性检验的基本思想卡方统计量0.1%把握认
为A与B无关1%把握认为A与B无关99.9%把握认
为A与B有关99%把握认
为A与B有关90%把握认
为A与B有关10%把握认为
A与B无关没有充分的依据显示A与B有关,但也不能显示A与B无关 例4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下表:
(1)利用等高条形图比较两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
0.9
1
0
0.5
0.40.30.20.10.60.70.8优质品非优质品乙厂甲厂从等高条形图可以看出甲厂捡出的优质品的比例比乙厂的比例大得多. (6分)(2)
(8分)
课堂训练B2.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?解:根据题目所给的数据得到如下列联表:因为1.871×10-4<2.706,所以,在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.3.观察下列各图,其中两个分类变量x,y之间关系最强的是 ( )选D.D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.D 4.分类变量X和Y的列联表如下,则下列说法中正确的是( )A. 越小,说明X与Y的相关性越弱
B. 越大,说明X与Y的相关性越强
C. 越大,说明X与Y的相关性越强
D. 越接近于0,说明X与Y的相关性越强解析】选C.因为k当(ad-bc)2越大时,k越大,说明X与Y关系越强
.C5.下列命题中:①回归直线除了经过样本点的中心,还至少经过一个样本点;②将一组数据中的每个数都减去同一个数后,平均值有变化,方差没有变化;③对分类变量X与Y,它们的随机变量的观测值越小,“X与Y有关系”的把握程度越模型拟合的效果越好.其中正确命题的序号为
_________________.大;④比较两个模型的拟合效果时,如果模型残差平方和越小,则相应的相关指数 越大,该②④6.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与x的线性回归方程为
,则表中的m的值为( )A.45 B.50 C.55 D.60本中心点(5,50),则m=60,故选D.解析 因为线性回归方程为 恒过样课后作业见讲义1,2题1.下面是一个2×2列联表,则表中a,b处的值分别为( ) A.94,96 B.52,50 C.52,60 D.54,52选C.由题意知a+21=73,a+8=b,解得a=52,b=60
. 2. 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.解:(1)作出散点图如右图所示, 其曲线模型是(2)y与x之间的回归方程是:
解:(1)设年份x,需求量y( 万吨):代入所求回归直线方程中:练习1 .在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)作出散点图,你能从散点图中发现投入量x与产量y的一般规律吗?(2)求回归直线方程.(3)预测当投入量x=14时,产量y是多少?
0 1 2 3 解:(1)作出散点图如右图所示:
投入量x与产量y是线性正相关,
随着投入量x产量y逐渐增加。(2)从图中可以看出,各点散布在一条直线附近,即它们线性相关.(3)预测当产量x=14时,所需的投入量x是20.5.2、相关指数的计算例2 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
解:当x=0,1,2,3时, 解:当x=0,1,2,3时,0 1 2 3 相关指数越大,越接近于1,,模拟的拟合效果越好;相关指数越小,拟合的效果越差!3、回归方程的模型1.直线方程模型;
2.指数函数模型;
3.二次函数模型;
4.反比例函数模型;
5.对数函数模型.1.直线方程模型.2.指数函数模型.3.二次函数模型.4.反比例函数模型.5.对数函数模型. 例3 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.解:(1)作出散点图如右图所示:(2)y与x之间的回归方程是: 4.独立性检验的基本思想卡方统计量0.1%把握认
为A与B无关1%把握认为A与B无关99.9%把握认
为A与B有关99%把握认
为A与B有关90%把握认
为A与B有关10%把握认为
A与B无关没有充分的依据显示A与B有关,但也不能显示A与B无关 例4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下表:
(1)利用等高条形图比较两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
0.9
1
0
0.5
0.40.30.20.10.60.70.8优质品非优质品乙厂甲厂从等高条形图可以看出甲厂捡出的优质品的比例比乙厂的比例大得多. (6分)(2)
(8分)
课堂训练B2.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?解:根据题目所给的数据得到如下列联表:因为1.871×10-4<2.706,所以,在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.3.观察下列各图,其中两个分类变量x,y之间关系最强的是 ( )选D.D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.D 4.分类变量X和Y的列联表如下,则下列说法中正确的是( )A. 越小,说明X与Y的相关性越弱
B. 越大,说明X与Y的相关性越强
C. 越大,说明X与Y的相关性越强
D. 越接近于0,说明X与Y的相关性越强解析】选C.因为k当(ad-bc)2越大时,k越大,说明X与Y关系越强
.C5.下列命题中:①回归直线除了经过样本点的中心,还至少经过一个样本点;②将一组数据中的每个数都减去同一个数后,平均值有变化,方差没有变化;③对分类变量X与Y,它们的随机变量的观测值越小,“X与Y有关系”的把握程度越模型拟合的效果越好.其中正确命题的序号为
_________________.大;④比较两个模型的拟合效果时,如果模型残差平方和越小,则相应的相关指数 越大,该②④6.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与x的线性回归方程为
,则表中的m的值为( )A.45 B.50 C.55 D.60本中心点(5,50),则m=60,故选D.解析 因为线性回归方程为 恒过样课后作业见讲义1,2题1.下面是一个2×2列联表,则表中a,b处的值分别为( ) A.94,96 B.52,50 C.52,60 D.54,52选C.由题意知a+21=73,a+8=b,解得a=52,b=60
. 2. 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.解:(1)作出散点图如右图所示, 其曲线模型是(2)y与x之间的回归方程是:
