1.2.2 组合 课件(36张PPT)
文档属性
| 名称 | 1.2.2 组合 课件(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 11:34:14 | ||
图片预览






文档简介
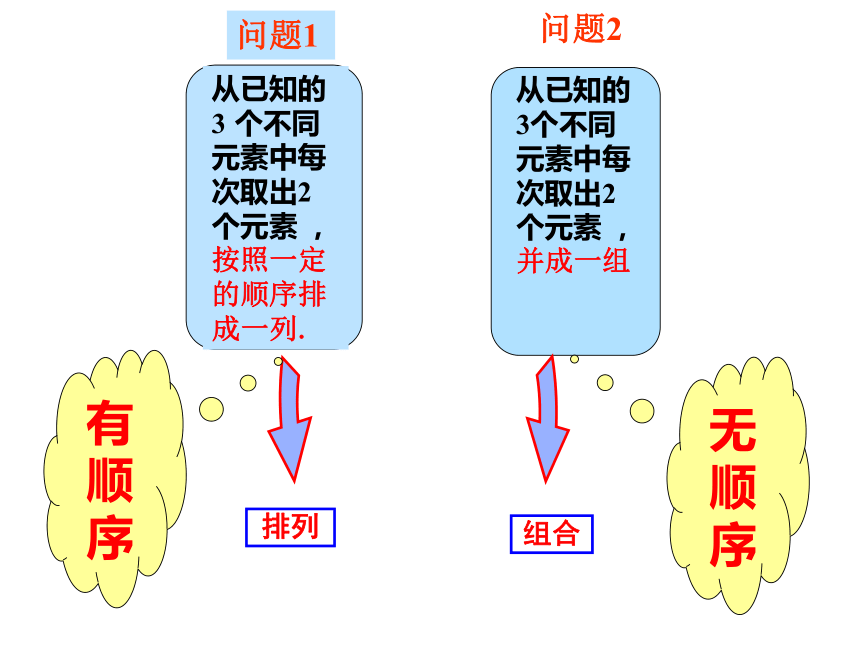
课件36张PPT。 1.2.2 组合问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?情境创设有
顺
序无
顺
序 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合. 排列与组合的概念有什么共同点与不同点? 概念讲解组合定义:组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.概念讲解思考一:ab与ba是相同的排列还是相同的组合?为什么?思考二:两个相同的排列有什么特点?两个相同的组合呢?概念理解构造排列分成两步完成,先取元素后排序;而构造组合就是其中一个步骤.思考三:组合与排列有联系吗?判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法??组合问题(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次??组合问题(5)从4个风景点中选出2个游览,有多少种不同的方法?组合问题(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法?排列问题组合问题组合是选择的结果,排列
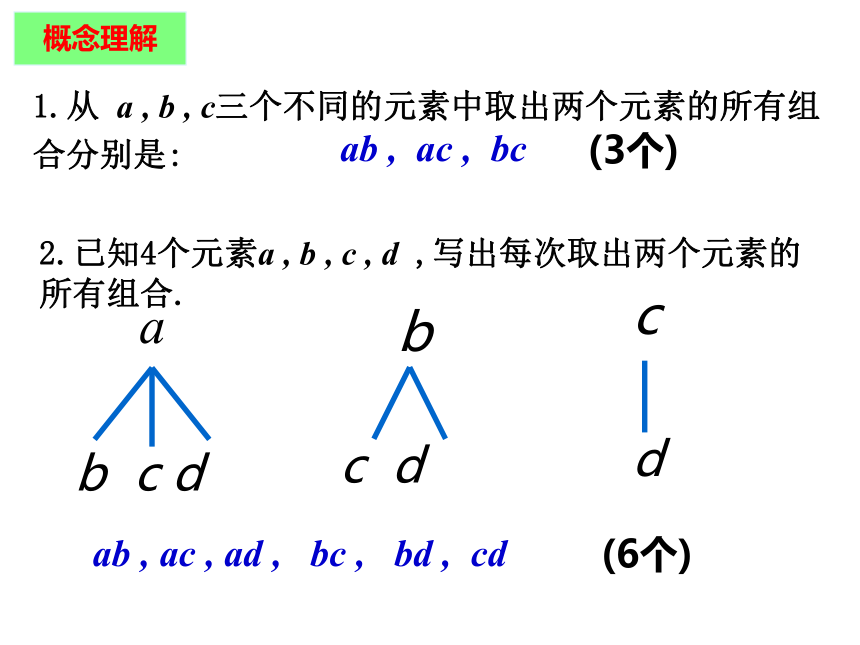
是先选择再排序的结果.1.从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:2.已知4个元素a , b , c , d ,写出每次取出两个元素的所有组合.概念理解 从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.如:从 a , b , c三个不同的元素中取出两个元素的所有组合个数是:如:从4个元素a 、b 、 c 、 d 中,每次取出两个
元素的所有组合个数是:概念讲解组合数:注意:
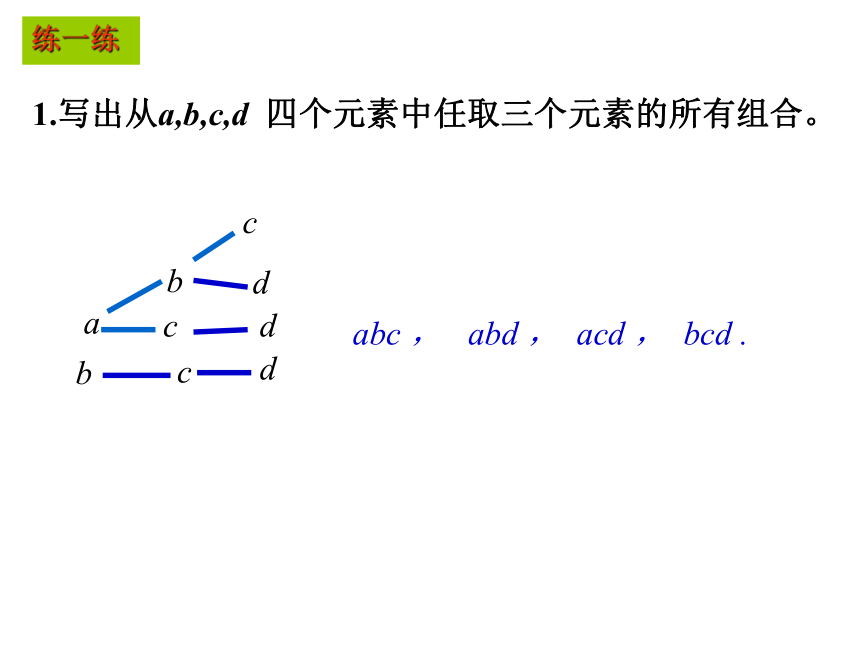
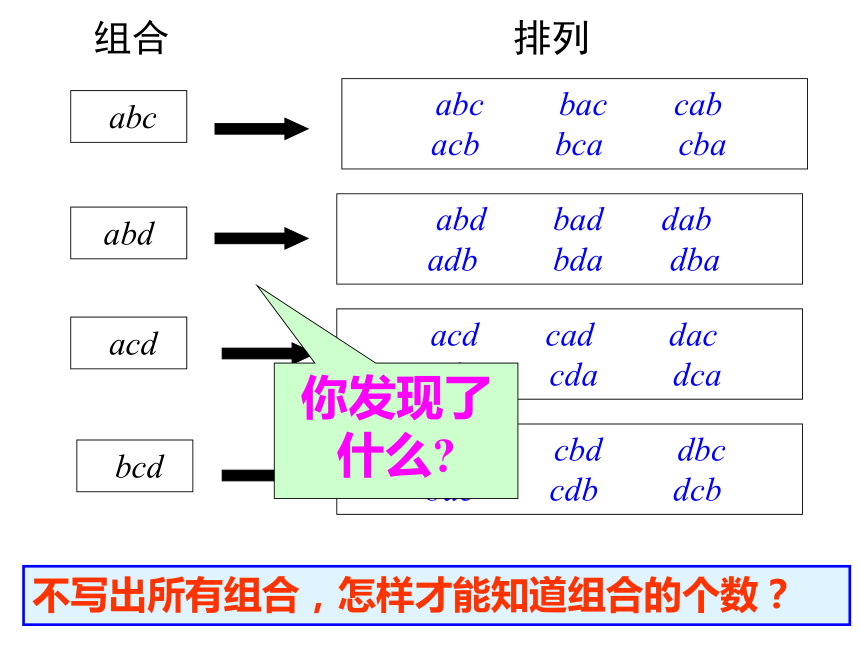
是一个数,应该把它与“组合”区别开来. 1.写出从a,b,c,d 四个元素中任取三个元素的所有组合。 abc , abd , acd , bcd .练一练组合排列 abc bac cab
acb bca cba abd bad dab
adb bda dba acd cad dac
adc cda dca bcd cbd dbc
bdc cdb dcb不写出所有组合,怎样才能知道组合的个数?你发现了什么?组合数公式 排列与组合是有区别的,但它们又有联系. 一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下两步: 第1步,先求出从这 个不同元素中取出 个元素的组合数 . 第2步,求每一个组合中 个元素的全排列数 . 根据分步计数原理,得到:因此: 这里 ,且 ,这个公式叫做组合数公式.概念讲解组合数公式: 从 n 个不同元中取出m个元素的排列数 概念讲解例题分析例2:一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛。按照足球比赛规则,比赛时一个足球队的上场队员是11人。问:
(1)这位教练从这17名学员中可以形成多少种学员上场方案?
(2)如果在选出11名上场队员时,还要确定其中的守门员,那么教练员有多少种方式做这件事情?例3.课本例7
(1)平面内有10个点,以其中每2个点为端点的线段共有多少条? (2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?例题分析(2)列出所有冠亚军的可能情况.(2)甲乙、甲丙、甲丁、乙丙、乙丁、丙丁
乙甲、丙甲、丁甲、丙乙、丁乙、丁丙(1) 甲乙、甲丙、甲丁、乙丙、乙丁、丙丁解:例5. (1)凸五边形有多少条对角线?(2)凸n( n>3)边形有多少条对角线?例7.
(1).从3,5,7,11这四个质数中任取两个相乘,可得到多少个不同的积?
(2) .从3,5,7,11这四个质数中任取两个相除,可得到多少个不同的商?解: (1).(2) l、这一节课学习了哪些知识点
2、在学习的过程中使用了哪些思想方 法
3、作业:p28A.13.14.15
例2知识要点4 组合的两个性质性质1 性质2例7:在100件产品中有98件合格品,2件次品。产品检验时,从100件产品中任意抽出3件。
(1)一共有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
(4)抽出的3件中至多有一件是次品的抽法有多少种?说明:“至少”“至多”的问题,通常用分类法或间接法求解。选人问题:变式练习按下列条件,从12人中选出5人,有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;选人问题:例8、某医院有内科医生12名,外科医生8名,现要派5人参加支边医疗队,至少要有1名内科医生和1名外科医生参加,有多少种选法?例9:某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语与日语的各1人,有多少种不同的选法?解:由于7+3=10>9,所以9人中必有1人既会英语又会日语.
(1)从只会英语的6人中选1人,只会日语的2人中选1人,
有N1=6×2=12
(2)既会英语又会日语的那位选定,其余8人中选1人,
有N2=1×8=8
由分类计数原理得N= N1+ N2=20.选人问题:课堂练习:2、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 。3、要从8名男医生和7名女医生中选5人组成一个医疗队,如果其中至少有2名男医生和至少有2名女医生,则不同的选法种数为( )4、从7人中选出3人分别担任学习委员、宣传委员、体育委员,则甲、乙两人不都入选的不同选法种数共有( )1、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 种 。99CD 例1:∠A的一边AB上有4个点,另一边AC上有5个点,连同∠A的顶点共10个点,以这些点为顶点,可以构成多少个三角形?解:方法1:把可构成的三角形可分成两类:
第一类,含点A的有 个;
第二类,不含点A的,又分为在AB上取两点在AC上取一点,和在AB上取一点AC上取两点,共有 个.与立体图形有关的问题: 根据加法原理,共可构成三角形的个数为 方法2:不考虑可否成为三角形,从这10个中点任取3个点共有 种方法,但仅在AB上或AC上任取3个点不能构成三角形,共有 种方法,
因此可构成三角形的个数为 例1:∠A的一边AB上有4个点,另一边AC上有5个点,连同∠A的顶点共10个点,以这些点为顶点,可以构成多少个三角形? 例2 . 四面体的顶点和各棱的中点共10个点。
(1)设一个顶点为A,从其他9点中取3个
点,使它们和点A在同一平面
上,不同的取法有多少种?
(2)在这10点中取4
个不共面的点,不同的
取法有多少种?与立体图形有关的问题: 1.(2009湖北卷文)从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有_____.
A.120种 B.96种 C.60种 D.48种
C2.(2009湖南卷文)某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为_____.
A.14 B.16 C.20 D.48B由间接得 ,故选B. 3.(2009全国卷Ⅰ文)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有_____.
A. 150种 B. 180种 C. 300种 D. 345种D本小题考查分类计算原理、分步计数原理、组合等问题 2.选择
(1) 从6双不同颜色的手套中任取4只,其中恰好有一双同色的手套的不同取法共有( )
A 480种 B 240种 C 180种 D 120种
(2) 从4台甲型和5台乙型电视机中任意取出3台,其中至少要有甲型和乙型电视机各1台,则不同的取法共有 ( )?.
? A.140种 B.84种 C.70种 D.35种?√√ (1)课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长.现从中选5人主持某种活动,依下列条件各有多少种选法??
①只有一名女生;?
②两队长当选;?
③至少有一名队长当选;
④至多有2名女生当选;?
⑤既要有队长,又要有女生当选.3.解答题④至多有两名女生含有三类:有2名女生、只有一名女生、没有女生.故选法为:
⑤分两类:
第一类女队长当选:
第二类女队长不当选:
故选法共有: ④至多有2名女生当选;
⑤既要有队长,又要有女生当选排列课堂小结
顺
序无
顺
序 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合. 排列与组合的概念有什么共同点与不同点? 概念讲解组合定义:组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.概念讲解思考一:ab与ba是相同的排列还是相同的组合?为什么?思考二:两个相同的排列有什么特点?两个相同的组合呢?概念理解构造排列分成两步完成,先取元素后排序;而构造组合就是其中一个步骤.思考三:组合与排列有联系吗?判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法??组合问题(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次??组合问题(5)从4个风景点中选出2个游览,有多少种不同的方法?组合问题(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法?排列问题组合问题组合是选择的结果,排列
是先选择再排序的结果.1.从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:2.已知4个元素a , b , c , d ,写出每次取出两个元素的所有组合.概念理解 从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.如:从 a , b , c三个不同的元素中取出两个元素的所有组合个数是:如:从4个元素a 、b 、 c 、 d 中,每次取出两个
元素的所有组合个数是:概念讲解组合数:注意:
是一个数,应该把它与“组合”区别开来. 1.写出从a,b,c,d 四个元素中任取三个元素的所有组合。 abc , abd , acd , bcd .练一练组合排列 abc bac cab
acb bca cba abd bad dab
adb bda dba acd cad dac
adc cda dca bcd cbd dbc
bdc cdb dcb不写出所有组合,怎样才能知道组合的个数?你发现了什么?组合数公式 排列与组合是有区别的,但它们又有联系. 一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下两步: 第1步,先求出从这 个不同元素中取出 个元素的组合数 . 第2步,求每一个组合中 个元素的全排列数 . 根据分步计数原理,得到:因此: 这里 ,且 ,这个公式叫做组合数公式.概念讲解组合数公式: 从 n 个不同元中取出m个元素的排列数 概念讲解例题分析例2:一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛。按照足球比赛规则,比赛时一个足球队的上场队员是11人。问:
(1)这位教练从这17名学员中可以形成多少种学员上场方案?
(2)如果在选出11名上场队员时,还要确定其中的守门员,那么教练员有多少种方式做这件事情?例3.课本例7
(1)平面内有10个点,以其中每2个点为端点的线段共有多少条? (2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?例题分析(2)列出所有冠亚军的可能情况.(2)甲乙、甲丙、甲丁、乙丙、乙丁、丙丁
乙甲、丙甲、丁甲、丙乙、丁乙、丁丙(1) 甲乙、甲丙、甲丁、乙丙、乙丁、丙丁解:例5. (1)凸五边形有多少条对角线?(2)凸n( n>3)边形有多少条对角线?例7.
(1).从3,5,7,11这四个质数中任取两个相乘,可得到多少个不同的积?
(2) .从3,5,7,11这四个质数中任取两个相除,可得到多少个不同的商?解: (1).(2) l、这一节课学习了哪些知识点
2、在学习的过程中使用了哪些思想方 法
3、作业:p28A.13.14.15
例2知识要点4 组合的两个性质性质1 性质2例7:在100件产品中有98件合格品,2件次品。产品检验时,从100件产品中任意抽出3件。
(1)一共有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
(4)抽出的3件中至多有一件是次品的抽法有多少种?说明:“至少”“至多”的问题,通常用分类法或间接法求解。选人问题:变式练习按下列条件,从12人中选出5人,有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;选人问题:例8、某医院有内科医生12名,外科医生8名,现要派5人参加支边医疗队,至少要有1名内科医生和1名外科医生参加,有多少种选法?例9:某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语与日语的各1人,有多少种不同的选法?解:由于7+3=10>9,所以9人中必有1人既会英语又会日语.
(1)从只会英语的6人中选1人,只会日语的2人中选1人,
有N1=6×2=12
(2)既会英语又会日语的那位选定,其余8人中选1人,
有N2=1×8=8
由分类计数原理得N= N1+ N2=20.选人问题:课堂练习:2、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 。3、要从8名男医生和7名女医生中选5人组成一个医疗队,如果其中至少有2名男医生和至少有2名女医生,则不同的选法种数为( )4、从7人中选出3人分别担任学习委员、宣传委员、体育委员,则甲、乙两人不都入选的不同选法种数共有( )1、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 种 。99CD 例1:∠A的一边AB上有4个点,另一边AC上有5个点,连同∠A的顶点共10个点,以这些点为顶点,可以构成多少个三角形?解:方法1:把可构成的三角形可分成两类:
第一类,含点A的有 个;
第二类,不含点A的,又分为在AB上取两点在AC上取一点,和在AB上取一点AC上取两点,共有 个.与立体图形有关的问题: 根据加法原理,共可构成三角形的个数为 方法2:不考虑可否成为三角形,从这10个中点任取3个点共有 种方法,但仅在AB上或AC上任取3个点不能构成三角形,共有 种方法,
因此可构成三角形的个数为 例1:∠A的一边AB上有4个点,另一边AC上有5个点,连同∠A的顶点共10个点,以这些点为顶点,可以构成多少个三角形? 例2 . 四面体的顶点和各棱的中点共10个点。
(1)设一个顶点为A,从其他9点中取3个
点,使它们和点A在同一平面
上,不同的取法有多少种?
(2)在这10点中取4
个不共面的点,不同的
取法有多少种?与立体图形有关的问题: 1.(2009湖北卷文)从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有_____.
A.120种 B.96种 C.60种 D.48种
C2.(2009湖南卷文)某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为_____.
A.14 B.16 C.20 D.48B由间接得 ,故选B. 3.(2009全国卷Ⅰ文)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有_____.
A. 150种 B. 180种 C. 300种 D. 345种D本小题考查分类计算原理、分步计数原理、组合等问题 2.选择
(1) 从6双不同颜色的手套中任取4只,其中恰好有一双同色的手套的不同取法共有( )
A 480种 B 240种 C 180种 D 120种
(2) 从4台甲型和5台乙型电视机中任意取出3台,其中至少要有甲型和乙型电视机各1台,则不同的取法共有 ( )?.
? A.140种 B.84种 C.70种 D.35种?√√ (1)课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长.现从中选5人主持某种活动,依下列条件各有多少种选法??
①只有一名女生;?
②两队长当选;?
③至少有一名队长当选;
④至多有2名女生当选;?
⑤既要有队长,又要有女生当选.3.解答题④至多有两名女生含有三类:有2名女生、只有一名女生、没有女生.故选法为:
⑤分两类:
第一类女队长当选:
第二类女队长不当选:
故选法共有: ④至多有2名女生当选;
⑤既要有队长,又要有女生当选排列课堂小结
