1.3.2 “杨辉三角”与二项式系数的性质 课件(18张PPT)
文档属性
| 名称 | 1.3.2 “杨辉三角”与二项式系数的性质 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 484.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 00:00:00 | ||
图片预览



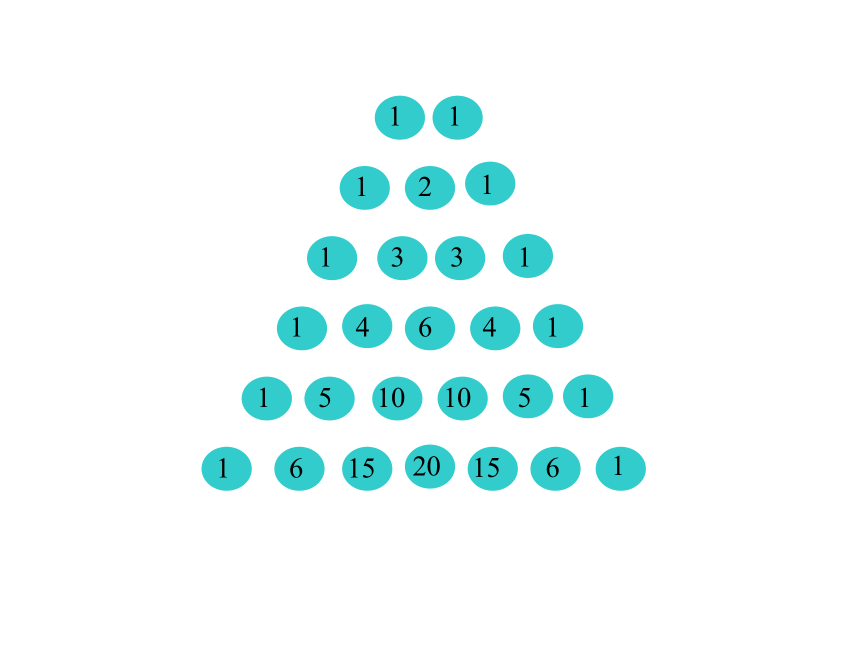
文档简介
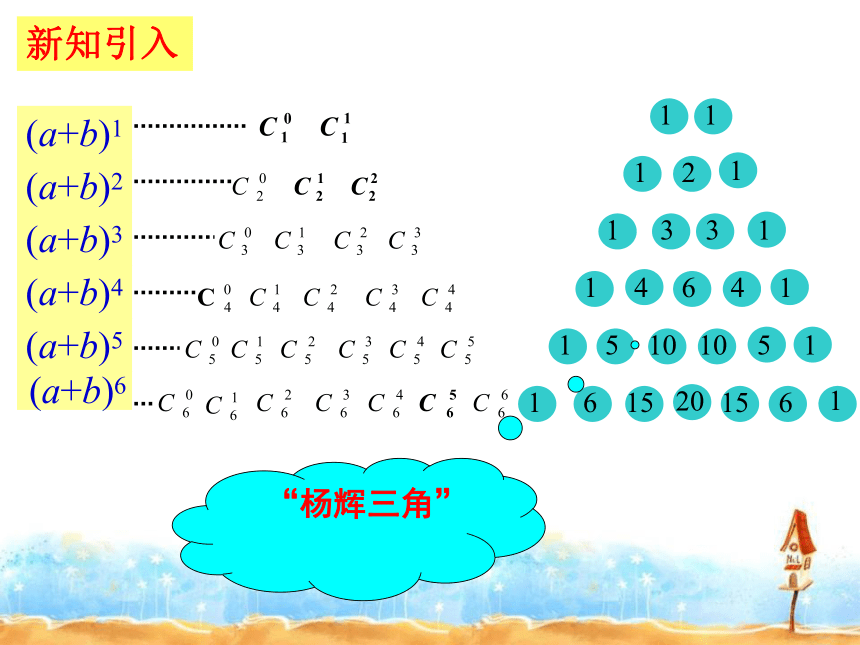
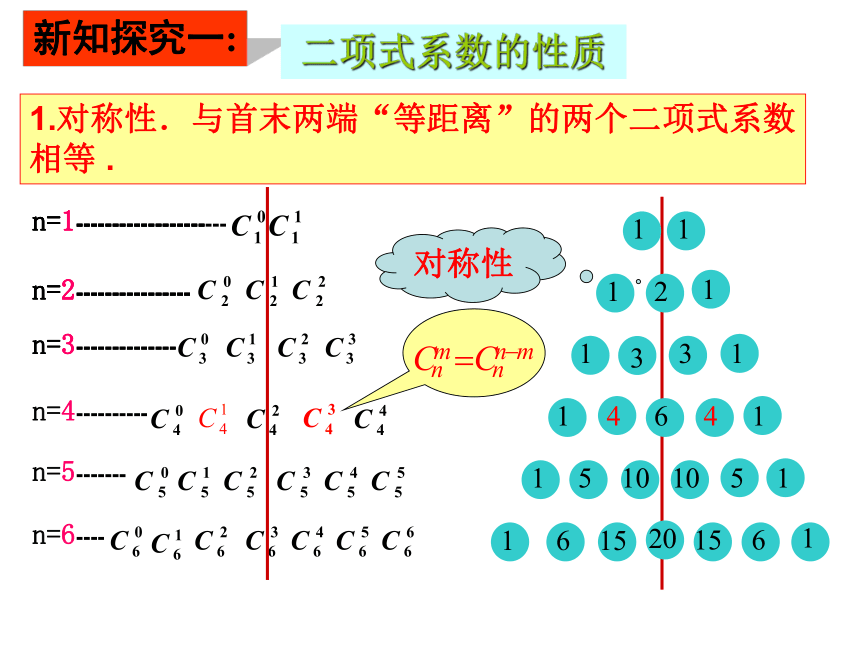
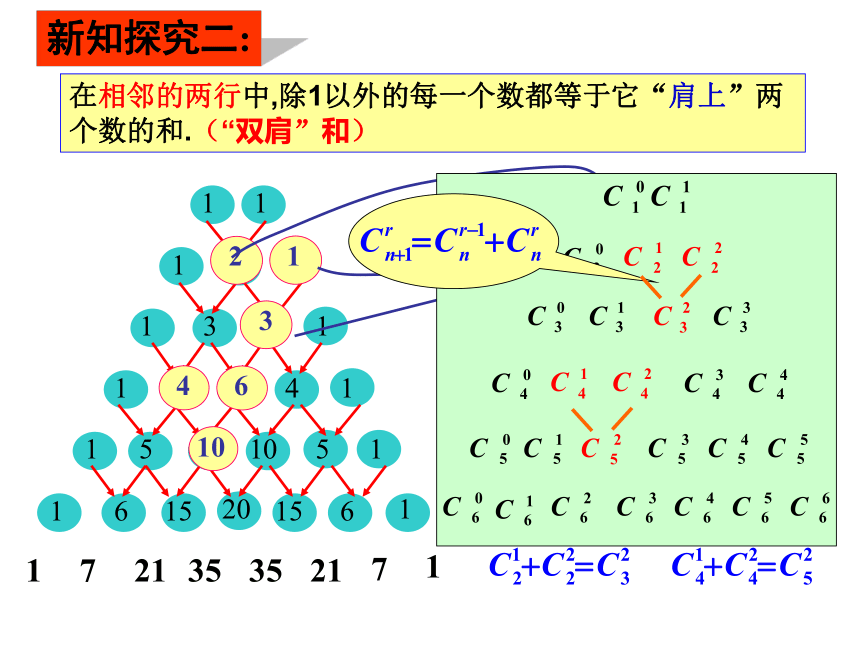
课件18张PPT。§1.3.2 “杨辉三角”与二项式系数的性质普通高中课程标准人教A版数学选修2-3复习回顾 二项式定理:二项式系数通项组合数两个性质:新知引入 “杨辉三角”(a+b)6杨辉三角 此表在我国南宋数学家杨辉1261年所著的《详解九章算法》里就已经出现,并且北宋数学家贾宪(约公元11 世纪)已使用过它.杨辉(南宋) 在欧洲,这个表被认为是法国数学家帕斯卡(1623-1662)首先发现的,他们把这个表叫做帕斯卡三角. 杨辉三角的发现要比欧洲早五百年左右.n=6----n=5-------n=4----------对称性新知探究一:n=3--------------n=1------------------n=2----------------n=1------------------n=2----------------n=3--------------n=1---------------------n=2----------------1.对称性.与首末两端“等距离”的两个二项式系数相等 .二项式系数的性质4+6=10新知探究二:173521135217纵向:相邻两行的数有什么关系? 在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.(“双肩”和)当n为偶数如2、4、6时,中间一项最大2.增减性与最大值 新知探究三:横向:每行系数大小变化趋势?当n为奇数如1、3、5时,中间两项最大n=6---n=5------n=4---------n=3------------n=1--------------------n=2---------------n=1--------------------n=2---------------n=3------------n=1--------------------n=2---------------n=6---n=5------n=4---------n=3------------n=1--------------------n=2--------------- 可知,当 时,二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。增减性与最大值理论推导证明:(法一) 可知,当 时,二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。增减性与最大值理论推导证明:(法二)定义域为 { 0, 1, 2, … , n }.其图象是7个孤立点.函数角度图象法直线 作为对称轴将图象分成对称的两部分 深入探究当n= 6时,nOOn当n是偶数时,中间的一项 取得最大值.当n是奇数时,中间的两项 和 相等,且同时取得最大值.n为奇数;
如n=7n为偶数;如n=64336710203020156新知探究四:计算各行二项式系数的和,你能发现什么规律?n=6---n=5----------n=4--------------n=3-------------------n=1----------------------------n=2-----------------------n3.各二项式系数的和 二项式系数的性质赋值法例3 试证:在 展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.典例解析 即在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.在二项式定理中,令 ,则: 证明:赋值法1.若 的展开式中,第三项与第七项的二项式系数相等,则n=_____学以致用82.在 的展开式中,二项式系数的最大值
为 .(结果用组合数表示) 3.在 的展开式中,二项式系数的最大值
为 .(结果用组合数表示) 掌握三个性质体现两种思想数形结合与函数的思想二项式系数的三个性质主题:“杨辉三角”与二项式系数的性质学会一个方法赋值法 作业题:习题1.3 A组6、7、8. 课后探究:“杨辉三角”中的一些秘密.课后作业
如n=7n为偶数;如n=64336710203020156新知探究四:计算各行二项式系数的和,你能发现什么规律?n=6---n=5----------n=4--------------n=3-------------------n=1----------------------------n=2-----------------------n3.各二项式系数的和 二项式系数的性质赋值法例3 试证:在 展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.典例解析 即在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.在二项式定理中,令 ,则: 证明:赋值法1.若 的展开式中,第三项与第七项的二项式系数相等,则n=_____学以致用82.在 的展开式中,二项式系数的最大值
为 .(结果用组合数表示) 3.在 的展开式中,二项式系数的最大值
为 .(结果用组合数表示) 掌握三个性质体现两种思想数形结合与函数的思想二项式系数的三个性质主题:“杨辉三角”与二项式系数的性质学会一个方法赋值法 作业题:习题1.3 A组6、7、8. 课后探究:“杨辉三角”中的一些秘密.课后作业
