2.1.1 离散型随机变量 课件(22张PPT)
文档属性
| 名称 | 2.1.1 离散型随机变量 课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 730.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 11:37:32 | ||
图片预览







文档简介
课件22张PPT。离散型随机变量及其分布列出现的点数可以用数字1,2,3,4,5,6表示.掷一枚骰子时,出现的点数如何表示?那么掷一枚硬币的结果是否也可以用数字来表示呢?
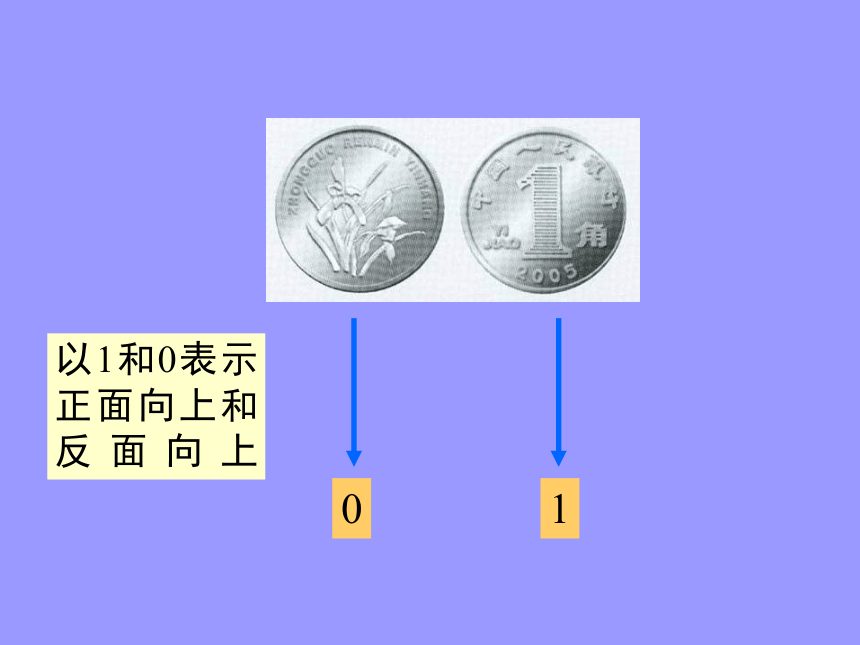
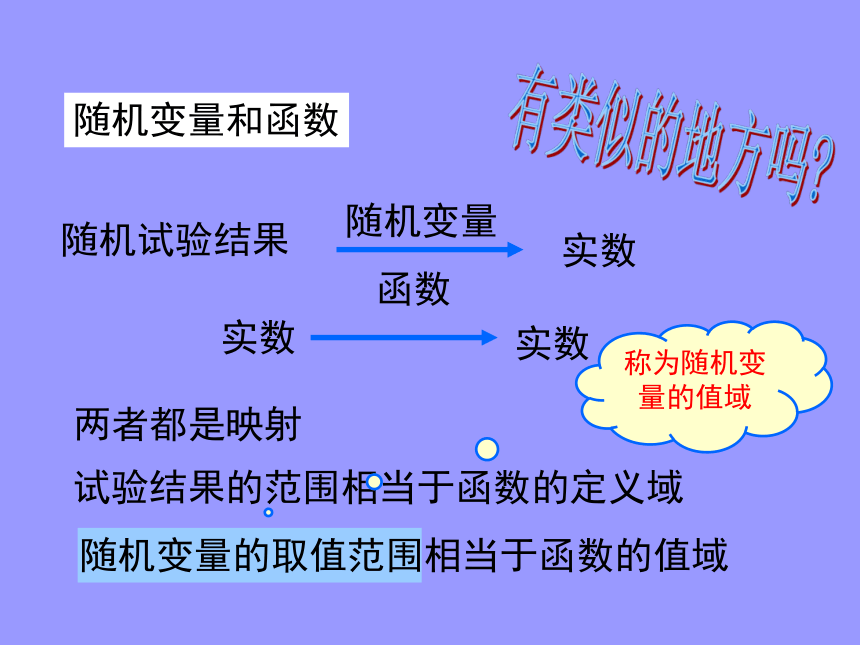
以1和0表示正面向上和反面向上某人射击一 次,可能出现命中0环,命中1环,…,命中10环等结果,可能出现的结果可能由0, 1,……10这11个数表示.某次产品检验,在可能含有次品的100件产品中任意抽取4件,那么其中含有的次品可能是0件,1件,2件,3件,4件,即可能出现的结果可以由0,1,2,3,4这5个数表示 我们确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果的变化而变化.随着试验结果变化而变化的变量称为随机变量随机变量常用字母 X ,Y ,? ,? ...表示随机变量和函数有类似的地方吗?两者都是映射试验结果的范围相当于函数的定义域随机变量的取值范围相当于函数的值域称为随机变量的值域某次产品检验,在可能含有次品的100件产品中任意抽取4件,可能含有次品件数X是一随机变量其值域{0,1,2,3,4}说明下列随机变量所取值所表示的含义抽出0件次品抽出4件次品抽出3件以下次品写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果 ξ可取3,4,5
ξ=3,表示取出的3个球的编号为1,2,3;
ξ=4,表示取出的3个球的编号为1,2,4或1,3,4或2,3,4;
ξ=5,表示取出的3个球的编号为1,2,5或1,3,5或1,4,5或2,3,5或2,4,5或3,4,5 一 袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出3只球,被取出的球的最大号码数ξ;??? ??解所有取值可以一一列出的随机变量,称为离散型随机变量 离散型随机变量:某人射击一次可能出现命中环数 X
某网页在24小时内被浏览的次数 Y
某单位的电话在1时间内收到的呼叫次数? 电灯泡的寿命X是离散型随机变量吗?电灯泡的寿命X可能取值是任何一个非负实数不能一一列出所以不是离散型随机变量恰当定义随机变量实际生活中只关心电灯泡的使用寿命是否超过1 000小时例1 下列随机试验的结果能否用离散型随机变量表示?若能,请写出各随机变量可能的结果并说明这些值所表示的随机试验的结果.1)抛掷两枚骰子,所得点数之和
2)某足球队在5次点球中射进的球数;
3)任意抽取一瓶标有2500ml的饮料,其实际量与规定量之差. 抛掷两枚骰子各一 次,记第一 枚骰子掷出的点数与第二枚骰子掷出的点数的差为ξ,试问:“ξ> 4”表示的试验结果是什么?“ξ>4”表示第一 枚为6点,第二枚为1点 练习抛掷一枚骰子,所得的点数X有哪些值?X取每个值的概率是多少? ⑴列出了随机变量X的所有取值.
⑵求出了X 的每一个取值的概率. X的取值有1、2、3、4、5、6离散型随机变量的分布列一般地,若离散型随机变量X可能取的不同值为
x1, x2 , ..., xi , ..., xn ,
X取每一个值xi(i=1,2,...,n)的概率P(X=xi)=pi,有下列表格称为离散型随机变量X 的概率分布列,简称X的分布列也表示为 P(X=xi)=pi ,i=1,2,...,nx1 x2 ... xi ... xnp1 p2 ... pi ... pn离散型随机变量分布列的变化情况用图象表示如:掷骰子试验随机变量的取值概率注1、分布列的构成
①列出了随机变量X 的所有取值.
②求出了X 的每一个取值的概率.
2、分布列的性质
①pi≥0,i=1,2,...,n
②例2在掷一枚图钉的随机试验中,令如果针尖向上的概率为p,试写出随机变量X的分布列.两点 分布列针尖向下的概率为1-p随机变量X 的分布列是解2.设随机变量X的分布列为则a的值为 .1.设随机变量X的分布列如下:则p的值为 .练习当堂反馈作业课本习题2.1A组1~5题
以1和0表示正面向上和反面向上某人射击一 次,可能出现命中0环,命中1环,…,命中10环等结果,可能出现的结果可能由0, 1,……10这11个数表示.某次产品检验,在可能含有次品的100件产品中任意抽取4件,那么其中含有的次品可能是0件,1件,2件,3件,4件,即可能出现的结果可以由0,1,2,3,4这5个数表示 我们确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果的变化而变化.随着试验结果变化而变化的变量称为随机变量随机变量常用字母 X ,Y ,? ,? ...表示随机变量和函数有类似的地方吗?两者都是映射试验结果的范围相当于函数的定义域随机变量的取值范围相当于函数的值域称为随机变量的值域某次产品检验,在可能含有次品的100件产品中任意抽取4件,可能含有次品件数X是一随机变量其值域{0,1,2,3,4}说明下列随机变量所取值所表示的含义抽出0件次品抽出4件次品抽出3件以下次品写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果 ξ可取3,4,5
ξ=3,表示取出的3个球的编号为1,2,3;
ξ=4,表示取出的3个球的编号为1,2,4或1,3,4或2,3,4;
ξ=5,表示取出的3个球的编号为1,2,5或1,3,5或1,4,5或2,3,5或2,4,5或3,4,5 一 袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出3只球,被取出的球的最大号码数ξ;??? ??解所有取值可以一一列出的随机变量,称为离散型随机变量 离散型随机变量:某人射击一次可能出现命中环数 X
某网页在24小时内被浏览的次数 Y
某单位的电话在1时间内收到的呼叫次数? 电灯泡的寿命X是离散型随机变量吗?电灯泡的寿命X可能取值是任何一个非负实数不能一一列出所以不是离散型随机变量恰当定义随机变量实际生活中只关心电灯泡的使用寿命是否超过1 000小时例1 下列随机试验的结果能否用离散型随机变量表示?若能,请写出各随机变量可能的结果并说明这些值所表示的随机试验的结果.1)抛掷两枚骰子,所得点数之和
2)某足球队在5次点球中射进的球数;
3)任意抽取一瓶标有2500ml的饮料,其实际量与规定量之差. 抛掷两枚骰子各一 次,记第一 枚骰子掷出的点数与第二枚骰子掷出的点数的差为ξ,试问:“ξ> 4”表示的试验结果是什么?“ξ>4”表示第一 枚为6点,第二枚为1点 练习抛掷一枚骰子,所得的点数X有哪些值?X取每个值的概率是多少? ⑴列出了随机变量X的所有取值.
⑵求出了X 的每一个取值的概率. X的取值有1、2、3、4、5、6离散型随机变量的分布列一般地,若离散型随机变量X可能取的不同值为
x1, x2 , ..., xi , ..., xn ,
X取每一个值xi(i=1,2,...,n)的概率P(X=xi)=pi,有下列表格称为离散型随机变量X 的概率分布列,简称X的分布列也表示为 P(X=xi)=pi ,i=1,2,...,nx1 x2 ... xi ... xnp1 p2 ... pi ... pn离散型随机变量分布列的变化情况用图象表示如:掷骰子试验随机变量的取值概率注1、分布列的构成
①列出了随机变量X 的所有取值.
②求出了X 的每一个取值的概率.
2、分布列的性质
①pi≥0,i=1,2,...,n
②例2在掷一枚图钉的随机试验中,令如果针尖向上的概率为p,试写出随机变量X的分布列.两点 分布列针尖向下的概率为1-p随机变量X 的分布列是解2.设随机变量X的分布列为则a的值为 .1.设随机变量X的分布列如下:则p的值为 .练习当堂反馈作业课本习题2.1A组1~5题
