3.1 回归分析的基本思想及其初步应用 课件(18张PPT)
文档属性
| 名称 | 3.1 回归分析的基本思想及其初步应用 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 00:00:00 | ||
图片预览


文档简介
课件18张PPT。高二数学 选修2-3 第三章 统计案例2019年8月13日星期二回归分析
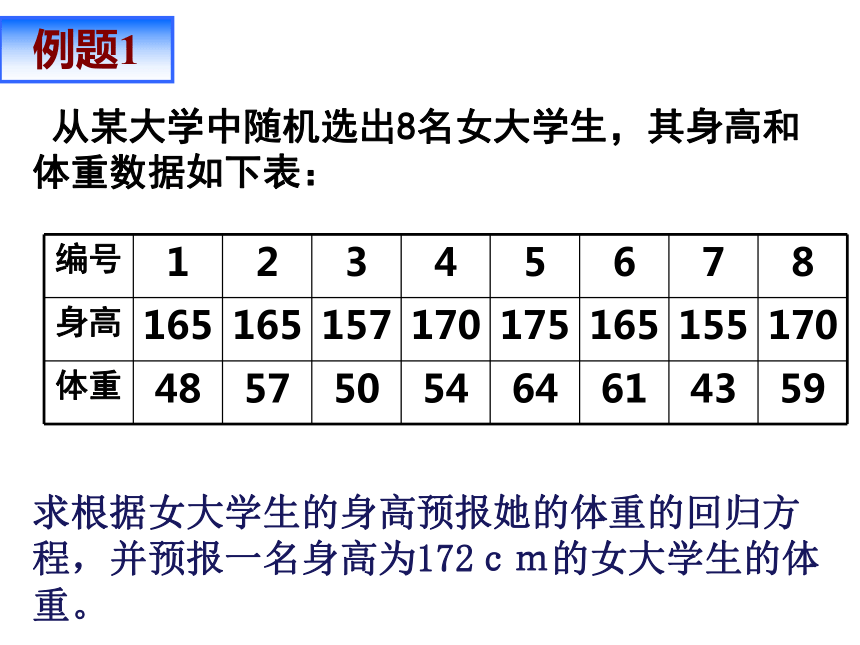
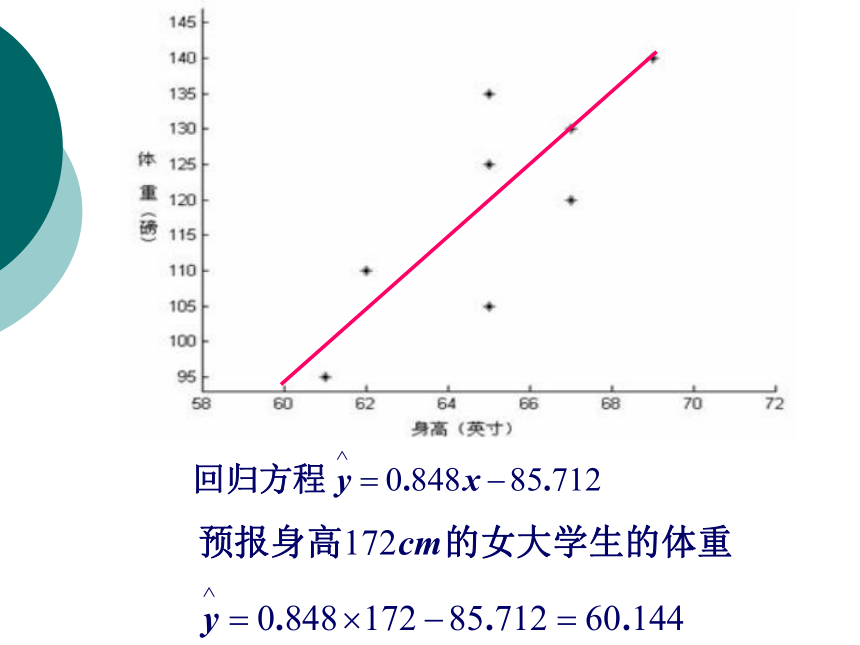
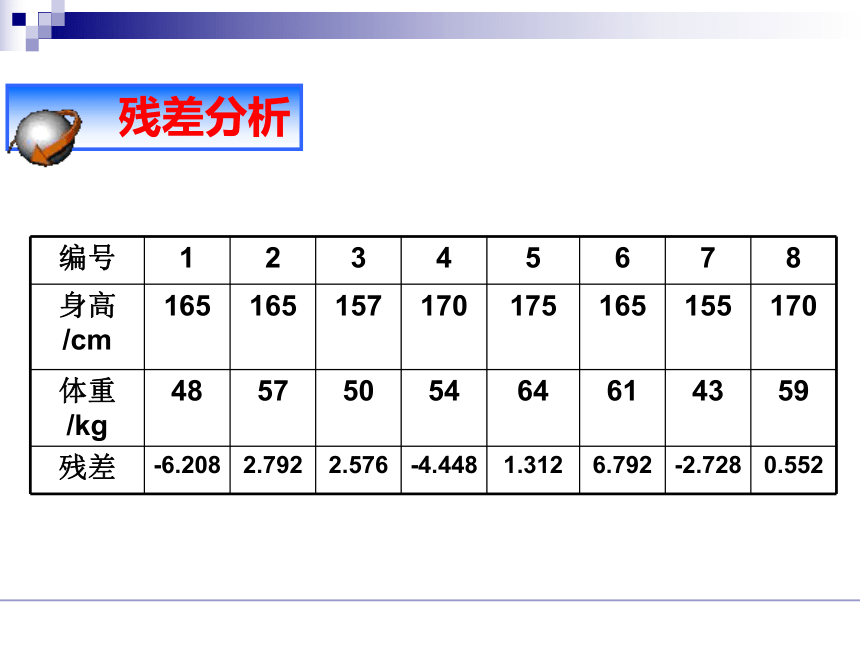
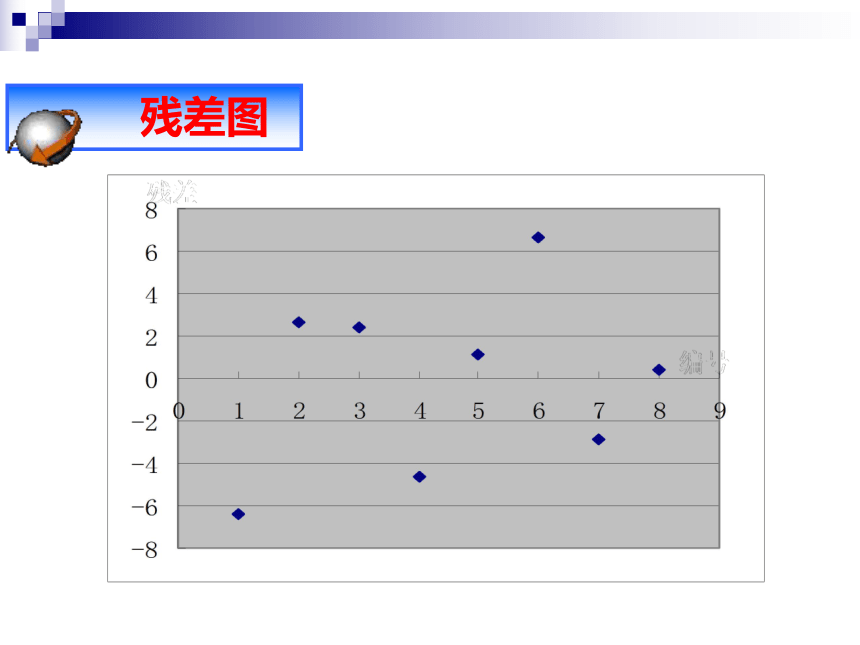
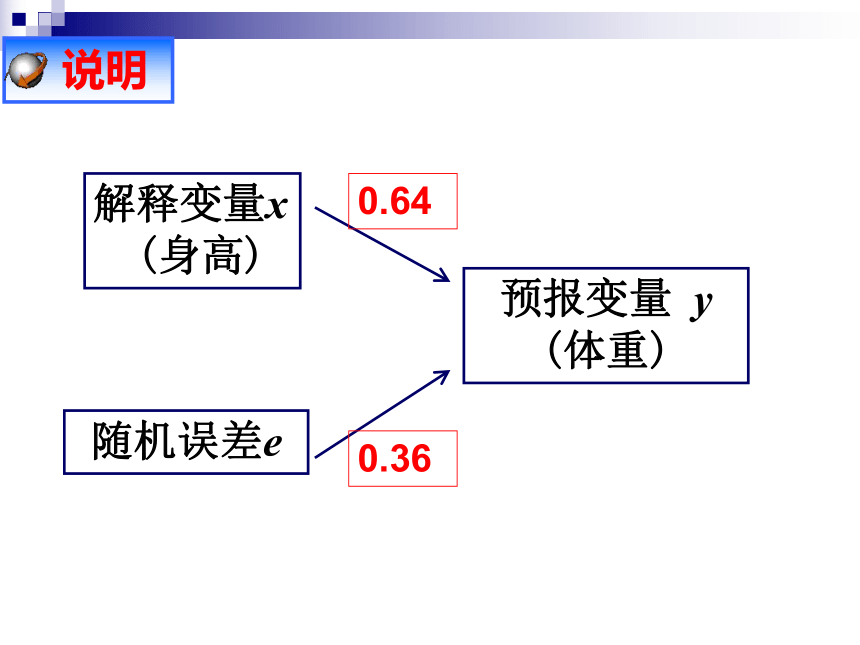
的基本思想及其初步应用 从某大学中随机选出8名女大学生,其身高和体重数据如下表:求根据女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。 例题1 残差分析 残差图解释变量x (身高)随机误差e预报变量 y (体重) 说明0.640.36用回归方程预报体重时应注意(1)模型适用的总体;
(2)模型的时间性;
(3)样本的取值范围对模型的影响;
(4)预报结果的正确理解。 说明一只红铃虫的产卵数y与温度x有关,现收集了7组观测数据,试建立y与x之间的回归方程例题21)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析. 小结建立回归模型的基本步骤:[答案] C 练习
2.在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98
B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50
D.模型4的相关指数R2为0.25
[答案] A 练习 练习4、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下: (1)建立回归模型,并残差分析,计算相关指数;
(2)你认为这个模型能较好地刻画零件数和加工时间的关系吗? 练习 [解] (1) 散点图,如图所示.残差数据如下表:以零件数为横坐标,残差为纵坐标画出残差图如图所示.回归分析知识结构图 总结
的基本思想及其初步应用 从某大学中随机选出8名女大学生,其身高和体重数据如下表:求根据女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。 例题1 残差分析 残差图解释变量x (身高)随机误差e预报变量 y (体重) 说明0.640.36用回归方程预报体重时应注意(1)模型适用的总体;
(2)模型的时间性;
(3)样本的取值范围对模型的影响;
(4)预报结果的正确理解。 说明一只红铃虫的产卵数y与温度x有关,现收集了7组观测数据,试建立y与x之间的回归方程例题21)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析. 小结建立回归模型的基本步骤:[答案] C 练习
2.在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98
B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50
D.模型4的相关指数R2为0.25
[答案] A 练习 练习4、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下: (1)建立回归模型,并残差分析,计算相关指数;
(2)你认为这个模型能较好地刻画零件数和加工时间的关系吗? 练习 [解] (1) 散点图,如图所示.残差数据如下表:以零件数为横坐标,残差为纵坐标画出残差图如图所示.回归分析知识结构图 总结
