3.1回归分析的基本思想及其初步应用 课件(15张PPT)
文档属性
| 名称 | 3.1回归分析的基本思想及其初步应用 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1001.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 11:54:27 | ||
图片预览



文档简介
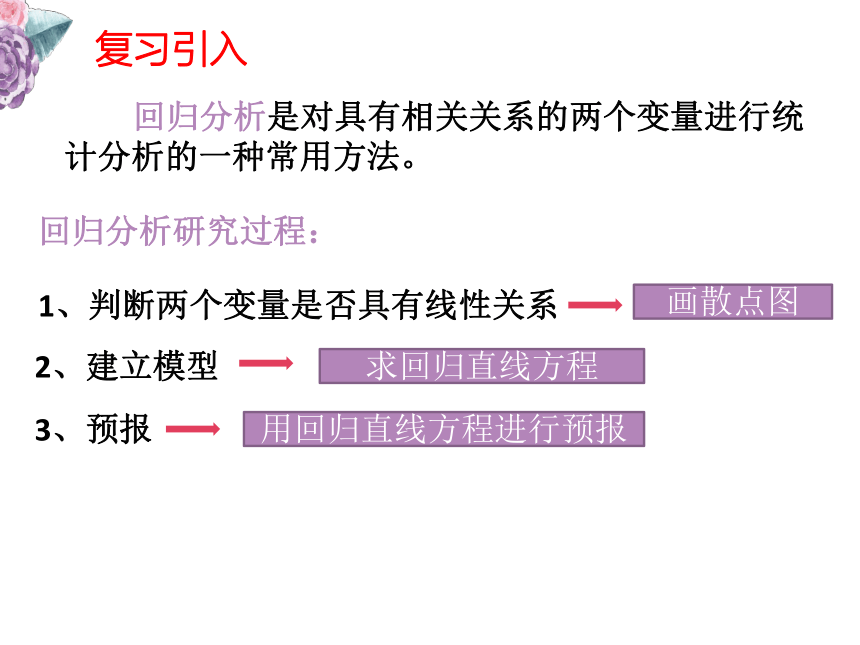
课件15张PPT。3.1回归分析的基本思想及其初步应用(1)选修2-3复习引入 回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法。1、判断两个变量是否具有线性关系
回归分析研究过程:画散点图2、建立模型求回归直线方程3、预报用回归直线方程进行预报复习引入:求回归直线方程对于一组具有线性相关关系的数据
我们知道其回归直线 的斜率和截距的最小二乘估计分别为
其中 称为样本点的中心
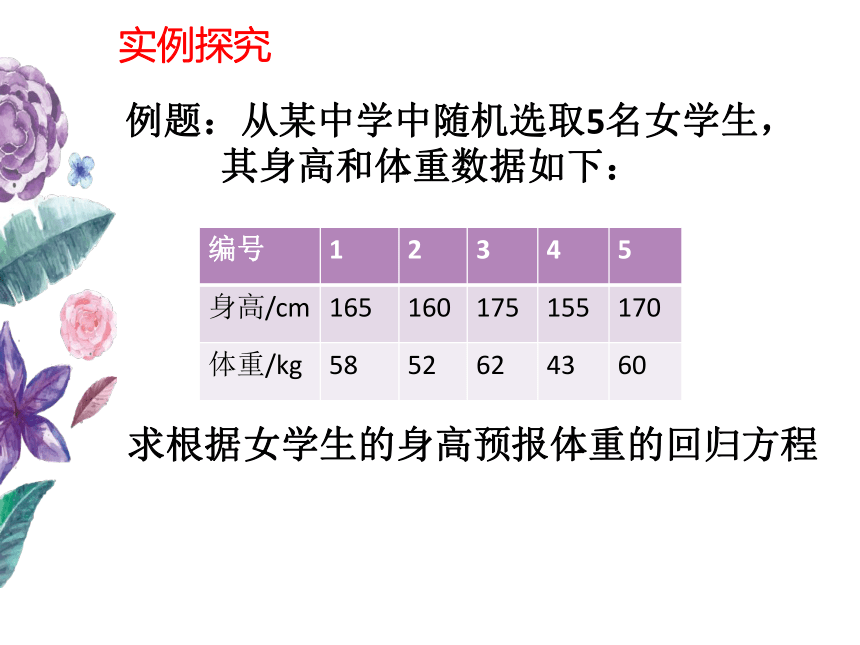
实例探究例题:从某中学中随机选取5名女学生,
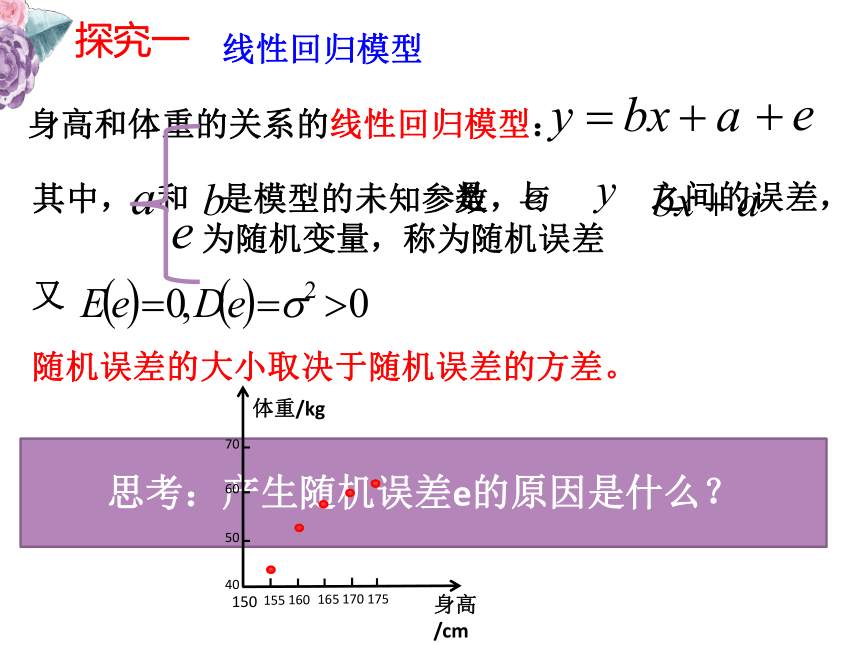
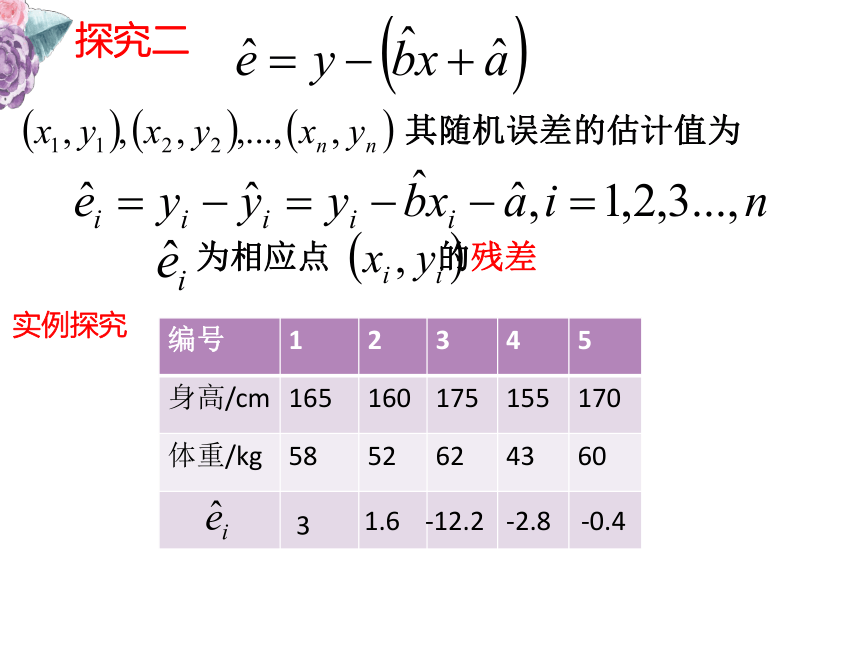
其身高和体重数据如下:求根据女学生的身高预报体重的回归方程探究一身高和体重的关系的线性回归模型:又随机误差的大小取决于随机误差的方差。 是 与 之间的误差,思考:产生随机误差e的原因是什么?线性回归模型探究二在线性回归模型中, 是用 预报真实值 的随机误差,它是一个不可观测的量,那么应该怎样研究随机误差呢?
估计值其随机误差的估计值为 为相应点 的残差探究二实例探究 3 1.6 -12.2 -2.8-0.4 3 1.6 -12.2 -2.8 -0.42、分布均匀在水平的带状区域,说明模型较为合适3、带状区域越窄,模型越合适,模型拟合程度越高,预报精度越高残差的作用1、直观地看出数据是否有误相关系数R21、越大,模型的拟合效果越好;
越小,模型的拟合效果越差。2、越接近于1,表示回归的效果越好广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元):例题应用(1)求根据广告费预报商品额的回归方程。你认为这个
模型能较好地刻画广告费和商品销售之间的关系
吗?请说明理由(2)请你做出残差图,根据残差图分析该模型的拟合
情况
注意:1、回归方程只适用于我们所研究的样本的总体2、我们所建立的回归方程一般都有时间性3、样本取值的范围会影响回归方程的适用范围4、不能期望回归方程得到的预报值就是预报变量的精准值1、判断两个变量是否具有线性关系
画散点图2、建立模型求回归直线方程3、预报用回归直线方程进行预报小结:建立回归模型的步骤画出残差图,分析是否有异常,检查数据是否有误或模型是否合适,或通过计算相关系数R2,分析模型是否合适。1234 3 1.6 -12.2 -2.8 -0.4例题:从某中学中随机选取5名女学生,
其身高和体重数据如下:思考请大家计算出相关系数R2,根据相关系数R2来分析模型的拟合程度实验作业请大家分小组收集20个同学的物理成绩和数学成绩,小组合作,建立一个回归模型,用物理成绩来预报数学成绩,并分析这个模型能否较好的刻画物理成绩和数学成绩的关系。要求:请提交数据及分析过程。作业:1、作业本:课本P89 习题3.1 第一题
2、完成配套练习
回归分析研究过程:画散点图2、建立模型求回归直线方程3、预报用回归直线方程进行预报复习引入:求回归直线方程对于一组具有线性相关关系的数据
我们知道其回归直线 的斜率和截距的最小二乘估计分别为
其中 称为样本点的中心
实例探究例题:从某中学中随机选取5名女学生,
其身高和体重数据如下:求根据女学生的身高预报体重的回归方程探究一身高和体重的关系的线性回归模型:又随机误差的大小取决于随机误差的方差。 是 与 之间的误差,思考:产生随机误差e的原因是什么?线性回归模型探究二在线性回归模型中, 是用 预报真实值 的随机误差,它是一个不可观测的量,那么应该怎样研究随机误差呢?
估计值其随机误差的估计值为 为相应点 的残差探究二实例探究 3 1.6 -12.2 -2.8-0.4 3 1.6 -12.2 -2.8 -0.42、分布均匀在水平的带状区域,说明模型较为合适3、带状区域越窄,模型越合适,模型拟合程度越高,预报精度越高残差的作用1、直观地看出数据是否有误相关系数R21、越大,模型的拟合效果越好;
越小,模型的拟合效果越差。2、越接近于1,表示回归的效果越好广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元):例题应用(1)求根据广告费预报商品额的回归方程。你认为这个
模型能较好地刻画广告费和商品销售之间的关系
吗?请说明理由(2)请你做出残差图,根据残差图分析该模型的拟合
情况
注意:1、回归方程只适用于我们所研究的样本的总体2、我们所建立的回归方程一般都有时间性3、样本取值的范围会影响回归方程的适用范围4、不能期望回归方程得到的预报值就是预报变量的精准值1、判断两个变量是否具有线性关系
画散点图2、建立模型求回归直线方程3、预报用回归直线方程进行预报小结:建立回归模型的步骤画出残差图,分析是否有异常,检查数据是否有误或模型是否合适,或通过计算相关系数R2,分析模型是否合适。1234 3 1.6 -12.2 -2.8 -0.4例题:从某中学中随机选取5名女学生,
其身高和体重数据如下:思考请大家计算出相关系数R2,根据相关系数R2来分析模型的拟合程度实验作业请大家分小组收集20个同学的物理成绩和数学成绩,小组合作,建立一个回归模型,用物理成绩来预报数学成绩,并分析这个模型能否较好的刻画物理成绩和数学成绩的关系。要求:请提交数据及分析过程。作业:1、作业本:课本P89 习题3.1 第一题
2、完成配套练习
