1.1 分类加法计数原理和分步乘法计数原理 课件(50张PPT)
文档属性
| 名称 | 1.1 分类加法计数原理和分步乘法计数原理 课件(50张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 538.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 12:13:24 | ||
图片预览






文档简介
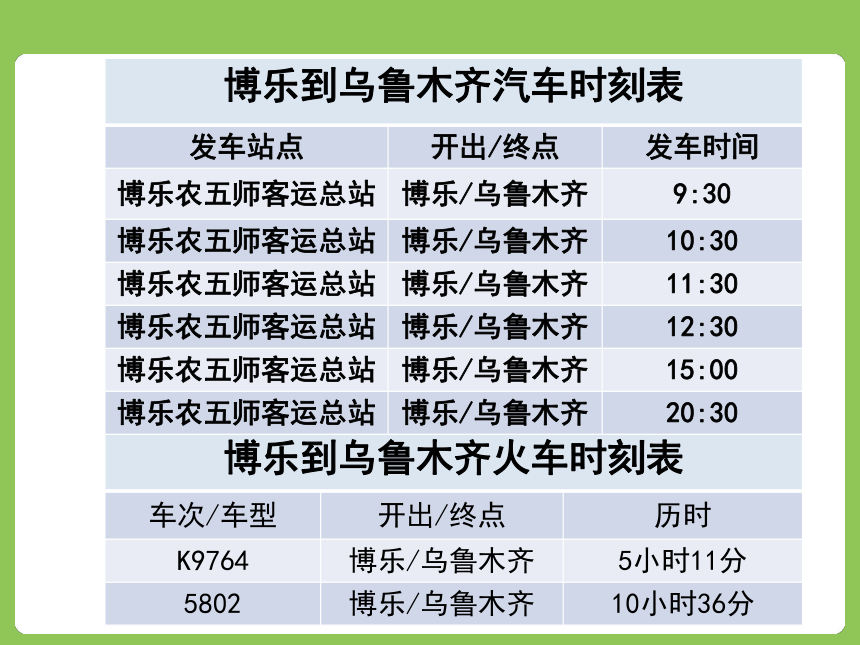
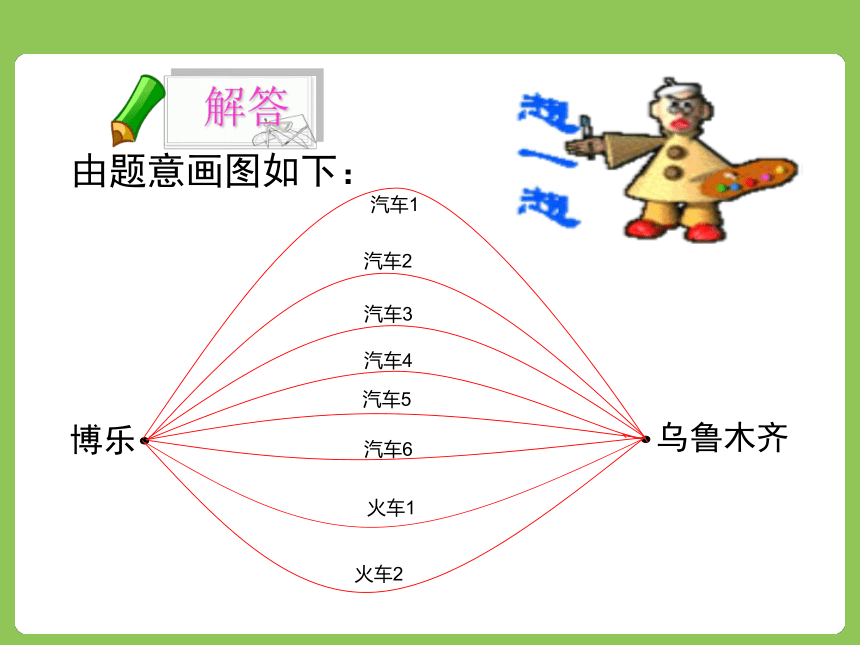
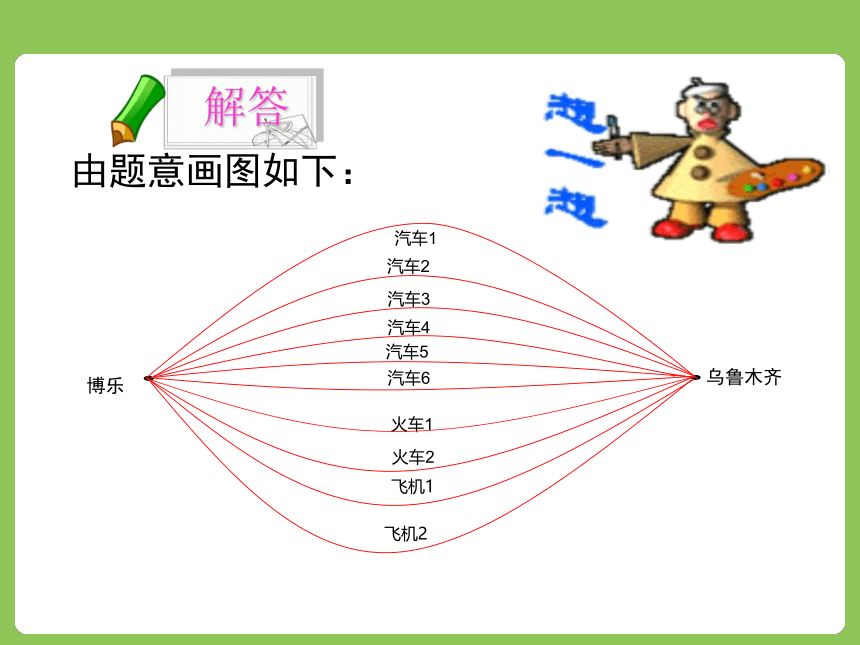
课件50张PPT。观看视频 高级中学某老师要从博乐到乌鲁木齐,可以乘火车,也可以乘汽车.乘坐表如下图. 乘坐这些交通工具从博乐到乌鲁木齐共有多少种不同的走法? 由题意画图如下:观察有什么特征解:
从博乐到乌鲁木齐有2类方案,
第一类方案:乘汽车,有6种方法;第二类方案:乘火车,有2种方法.所以从博乐到乌鲁木齐共有6+2=8种方法.分类加法计数原理
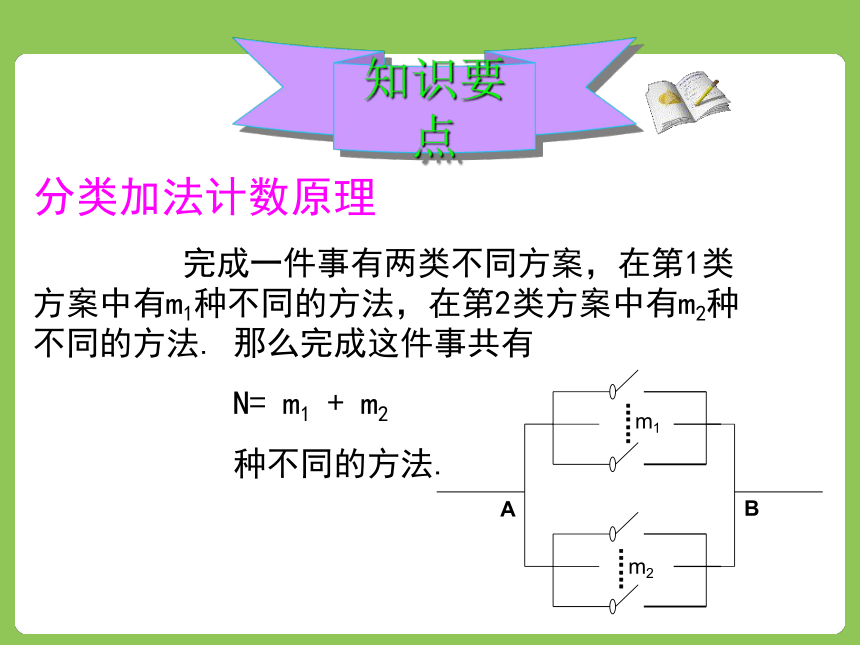
完成一件事有两类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法. 那么完成这件事共有
N= m1 + m2
种不同的方法.如果该老师还可以乘飞机去乌鲁木齐,航班时刻表如下图,那么该老师有多少种方法从博乐到达乌鲁木齐呢? 由题意画图如下:解:
从博乐到乌鲁木齐有3类方案,
第一类方案:乘汽车,有6种方法;
第二类方案:乘火车,有2种方法;
第三类方案:乘飞机,有2种方法.
所以从博乐到乌鲁木齐共有6+2+2=10种方法.观察有什么特征分类加法计数原理推广
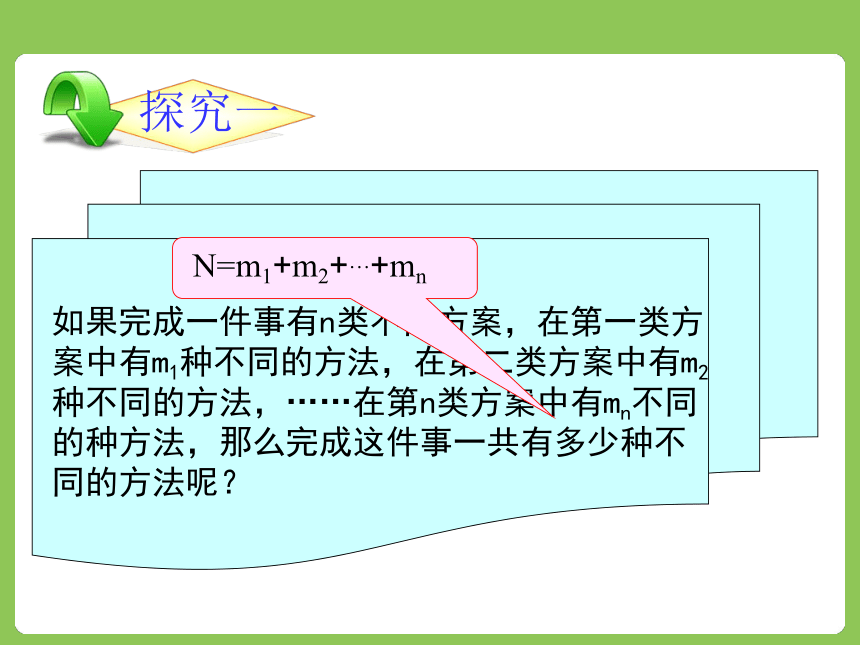
如果完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3类方案中有m3种不同的方法,那么完成这件事共有
N=m1+m2+m3
种不同的方法.
N=m1+m2+…+mn 12.9即将到来,农五师高级中学准备组织班级进行大合唱比赛,高二(5)班学生收集了高音类曲目和中音类曲目具体情况如下: 如果每班只能选一首曲目参加比赛,那么高二(5)班共有多少种选择呢?继续解答解:
高二(5)班有两类方案可以选择,
第一类方案,高音类,有4种方法
第二类方案,中音类,有5种方法
因此根据分类加法计数原理,高二(5)班可能的曲目共有
4+5=9(种)你能否发现这些问题有什么共同特征?该老师到达乌鲁木齐有10种方法,到达乌鲁木齐后要前往福州参加培训,可以乘火车也可以乘飞机, 到福州的乘坐表如图所示,那么该老师从博乐到乌鲁木齐再到福州共有多少种方法?105×解:
从博乐到福州有两步,
第一步:从博乐到乌鲁木齐,有10种方法;
第二步:从乌鲁木齐到福州,有5种方法.
所以从博乐到乌鲁木齐再到福州共有 10×5=50种方法.观察有什么特征分步乘法计数原理
完成一件事需要两个步骤,做第1步有m1种不同的方法,做第2步有 m2种不同的方法. 那么完成这件事共有
N=m1×m2
种不同的方法.如果该老师到达福州后要去离机场最近的锦江之星宾馆入住,共有三路公交车到达该宾馆。那么该老师有多少种方法从博乐到达锦江之星宾馆呢?解:
从博乐到福州锦江之星宾馆分三步,
第一步:从博乐到乌鲁木齐,有10种方法;
第二步:从乌鲁木齐到福州,有5种方法;
第三步:从福州到锦江之星宾馆有3种方法.
所以从博乐到锦江之星宾馆共有 10×5×3=150种方法.观察有什么特征分步乘法计数原理推广
如果完成一件事需要三个步骤,在第1步中有m1种不同的方法,在第2步中有m2不同的种方法,在第3步中有m3种不同的方法,那么完成这件事共有 N=m1×m2×m3
种不同的方法.
N=m1×m2×…×mn某班有3名学生准备参加校运动会的100米、200米、跳远、跳高四项比赛,如果每班每项限报一人,每人限报一项,则这3名学生参赛的不同方法有多少种?解析:
由于每班每人限报1人,
故当前面的学生选了某项之后,
后面的学生不能再报,
由分步乘法计数原理,
有4×3×2=24 种不同的参赛方法.你能否发现这些问题有什么共同特征?某同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆.
(1). 若他从这些参考书中带1本去图书馆,有多少种不同的带法?
(2).若带外语、数学、物理参考书各1本,有多少种不同的带法?
(3).若从这些参考书中选2本不同学科的参考书带到图书馆,有多少种不同的带法?
解:从这些参考书中带1本书,有三类方案,
第一类,带外语书,有5种方法;
第二类,带数学书,有4种方法;
第三类,带物理书,有3种方法.
根据分类加法计数原理,不同取法的种数是
N=5+4+3=12种解:带3本不同的学科参考书,分成三个步骤完成:
第一步,带1本外语书,有5种方法;
第二步,带1本数学书,有4种方法;
第三步,带1本物理书,有3种方法.
根据分步乘法计数原理,不同取法的种数是
N=5×4×3=60解:从这些参考书中选择2本不同的参考书,可以分为三类完成:
第一类,带1本外语书和1本数学书,
有5×4=20种方法;
第二类,带1本外语书和1本物理书,
有5×3=15种方法;
第三类,带1本数学书和1本物理书,
有3×4=12种方法.
即选择2本不同的参考书共有20+15+12=47种方法.分类计数原理:分步计数原理:完成一件事有两类不同方案,在第1类方案中有m1 种不同的方法,在第2类方案中有 m2种不同的方法.那么完成这件事共有
N= m1 + m2
种不同的方法.完成一件事需要两个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法.那么完成这件事共有
N= m1 × m2
种不同的方法. 两个计数原理用来计算“完成一件事”的方法总数
分类完成
类类相加分步完成
步步相乘
每类方案中的每一种方法都能独立完成这件事
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
类类独立 不重不漏
步步相依 步骤完整
如图,要让电路从A从到B处接通,可有多少条不同的路径?
解:
电路从A到B处接通可以分为三类方案:
第一类方案:有3种方法;
第二类方案:有1种方法;
第三类方案:从A到B分为两步:
第一步中有2种方法;
第二步中有2种方法;
第三类方案中,共有2×2=4种方法.
所以,电路从A到B处通路共有3+1+4=8种方法.从甲地到乙地有2种走法,从乙地到丙地有4种走法,从甲地不经过乙地到丙地有3种走法,则从甲地到丙地的不同的走法共有 多少种不同的走法.
解:从甲地到丙地可以分成两类完成:
第一类,从甲地经过乙地到丙地;
又分为两步,第一步,从甲地到乙地,共有2种走法;
第二步,从乙地到丙地,有4种方法;
根据分步计数原理,第一类中,从甲地到丙地共有
2×4=8种走法;
第二类,从甲地不经过乙地到丙地,共有3种走法.
根据分类加法计数原理,不同走法的种数是
N=8+3=11 种在A、B两区域内可以选择0~9内的任意整数,当A区域内的数比B区域内的数大时,共有多少种结果?利用分类计数原理解决问题: 第一类,A区域的数字为1,B区域上的数字有1种选法;
第二类,A区域的数字为2,B区域上的数字有2种选法;
第三类,A区域的数字为3,B区域上的数字有3种选法;
……
第九类,A区域的数字为9,B区域的数字有9种选法.
根据分类相加计数原理,A区域内的数比B区域内的数大的有
1+2+3+……+9=45种结果.
利用对称性解决问题:………… 共有100种情况,其中有10种是相同的,
100-10=90, A区域比B区域大的共有 90÷2=45种结果.利用坐标法解决问题:x<yx>yx大于y的部分共有45个整数点,所有A区域比B区域大的两位数共有45种结果如图所示,A、B、C、D四个区域,用红、黄、蓝三种颜色涂色,要求任意两个相邻区域的颜色各不相同,共有多少种不同的涂法?可以分为两类方案:
第一类方案:共用三种颜色去涂色
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;第三步,C区域选择一个颜色,有2种选择;第四步,D区域选择一个颜色,有1种选择.
第一类方案中,共有 3×2×2×1=12种方法.
第二类方案:共用了两种颜色去涂色
第一步,A区域选择一个颜色,有3种选择;第二步,B区域选择一个颜色,有2种选择;第三步,C区域与A区域选择颜色相同;
第四步,D区域与B区域选择相同.
第二类方案中,共有3×2×1×1=6种方法.
则共有12+6=18种方法ABCD方法一:如图所示,A、B、C、D四个区域,用红、黄、蓝三种颜色涂色,要求任意两个相邻区域的颜色各不相同,共有多少种不同的涂法?ABCD可以分为两类方案:
第一类方案:若A、C涂色相同
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;
第三步,C区域与A区域选择相同,有1种选择;
第四步,D区域选择一个颜色,有2种选择.
第一类方案中,共有 3×2×1×2=12种方法.
第二类方案:若A、C涂色不相同
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;
第三步,C区域选择一个颜色且与A颜色不同 ,有1种选择;
第四步,D区域选择一个颜色,有1种选择.
第二类方案中,共有3×2×1×1=6种方法.
则共有12+6=18种方法方法二: 在运用排列、组合方法时,经常要用到分类加法计数原理与分步乘法计数原理. 这节课,就是排列、组合方法的一个基础. 两个定义:分类加法计数原理、分步 乘法计数原理
三个思想:转化与化归、类比思想、 数形结合解答计数原理问题的一般思维过程:作业:
教材p12 1、2描述分类计数原理和分步计数原理的诗:●两大原理妙无穷
●解题应用各不同
●多思缜密最重要
●茫茫数理此中求再 见敬请指导.
从博乐到乌鲁木齐有2类方案,
第一类方案:乘汽车,有6种方法;第二类方案:乘火车,有2种方法.所以从博乐到乌鲁木齐共有6+2=8种方法.分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法. 那么完成这件事共有
N= m1 + m2
种不同的方法.如果该老师还可以乘飞机去乌鲁木齐,航班时刻表如下图,那么该老师有多少种方法从博乐到达乌鲁木齐呢? 由题意画图如下:解:
从博乐到乌鲁木齐有3类方案,
第一类方案:乘汽车,有6种方法;
第二类方案:乘火车,有2种方法;
第三类方案:乘飞机,有2种方法.
所以从博乐到乌鲁木齐共有6+2+2=10种方法.观察有什么特征分类加法计数原理推广
如果完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3类方案中有m3种不同的方法,那么完成这件事共有
N=m1+m2+m3
种不同的方法.
N=m1+m2+…+mn 12.9即将到来,农五师高级中学准备组织班级进行大合唱比赛,高二(5)班学生收集了高音类曲目和中音类曲目具体情况如下: 如果每班只能选一首曲目参加比赛,那么高二(5)班共有多少种选择呢?继续解答解:
高二(5)班有两类方案可以选择,
第一类方案,高音类,有4种方法
第二类方案,中音类,有5种方法
因此根据分类加法计数原理,高二(5)班可能的曲目共有
4+5=9(种)你能否发现这些问题有什么共同特征?该老师到达乌鲁木齐有10种方法,到达乌鲁木齐后要前往福州参加培训,可以乘火车也可以乘飞机, 到福州的乘坐表如图所示,那么该老师从博乐到乌鲁木齐再到福州共有多少种方法?105×解:
从博乐到福州有两步,
第一步:从博乐到乌鲁木齐,有10种方法;
第二步:从乌鲁木齐到福州,有5种方法.
所以从博乐到乌鲁木齐再到福州共有 10×5=50种方法.观察有什么特征分步乘法计数原理
完成一件事需要两个步骤,做第1步有m1种不同的方法,做第2步有 m2种不同的方法. 那么完成这件事共有
N=m1×m2
种不同的方法.如果该老师到达福州后要去离机场最近的锦江之星宾馆入住,共有三路公交车到达该宾馆。那么该老师有多少种方法从博乐到达锦江之星宾馆呢?解:
从博乐到福州锦江之星宾馆分三步,
第一步:从博乐到乌鲁木齐,有10种方法;
第二步:从乌鲁木齐到福州,有5种方法;
第三步:从福州到锦江之星宾馆有3种方法.
所以从博乐到锦江之星宾馆共有 10×5×3=150种方法.观察有什么特征分步乘法计数原理推广
如果完成一件事需要三个步骤,在第1步中有m1种不同的方法,在第2步中有m2不同的种方法,在第3步中有m3种不同的方法,那么完成这件事共有 N=m1×m2×m3
种不同的方法.
N=m1×m2×…×mn某班有3名学生准备参加校运动会的100米、200米、跳远、跳高四项比赛,如果每班每项限报一人,每人限报一项,则这3名学生参赛的不同方法有多少种?解析:
由于每班每人限报1人,
故当前面的学生选了某项之后,
后面的学生不能再报,
由分步乘法计数原理,
有4×3×2=24 种不同的参赛方法.你能否发现这些问题有什么共同特征?某同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆.
(1). 若他从这些参考书中带1本去图书馆,有多少种不同的带法?
(2).若带外语、数学、物理参考书各1本,有多少种不同的带法?
(3).若从这些参考书中选2本不同学科的参考书带到图书馆,有多少种不同的带法?
解:从这些参考书中带1本书,有三类方案,
第一类,带外语书,有5种方法;
第二类,带数学书,有4种方法;
第三类,带物理书,有3种方法.
根据分类加法计数原理,不同取法的种数是
N=5+4+3=12种解:带3本不同的学科参考书,分成三个步骤完成:
第一步,带1本外语书,有5种方法;
第二步,带1本数学书,有4种方法;
第三步,带1本物理书,有3种方法.
根据分步乘法计数原理,不同取法的种数是
N=5×4×3=60解:从这些参考书中选择2本不同的参考书,可以分为三类完成:
第一类,带1本外语书和1本数学书,
有5×4=20种方法;
第二类,带1本外语书和1本物理书,
有5×3=15种方法;
第三类,带1本数学书和1本物理书,
有3×4=12种方法.
即选择2本不同的参考书共有20+15+12=47种方法.分类计数原理:分步计数原理:完成一件事有两类不同方案,在第1类方案中有m1 种不同的方法,在第2类方案中有 m2种不同的方法.那么完成这件事共有
N= m1 + m2
种不同的方法.完成一件事需要两个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法.那么完成这件事共有
N= m1 × m2
种不同的方法. 两个计数原理用来计算“完成一件事”的方法总数
分类完成
类类相加分步完成
步步相乘
每类方案中的每一种方法都能独立完成这件事
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
类类独立 不重不漏
步步相依 步骤完整
如图,要让电路从A从到B处接通,可有多少条不同的路径?
解:
电路从A到B处接通可以分为三类方案:
第一类方案:有3种方法;
第二类方案:有1种方法;
第三类方案:从A到B分为两步:
第一步中有2种方法;
第二步中有2种方法;
第三类方案中,共有2×2=4种方法.
所以,电路从A到B处通路共有3+1+4=8种方法.从甲地到乙地有2种走法,从乙地到丙地有4种走法,从甲地不经过乙地到丙地有3种走法,则从甲地到丙地的不同的走法共有 多少种不同的走法.
解:从甲地到丙地可以分成两类完成:
第一类,从甲地经过乙地到丙地;
又分为两步,第一步,从甲地到乙地,共有2种走法;
第二步,从乙地到丙地,有4种方法;
根据分步计数原理,第一类中,从甲地到丙地共有
2×4=8种走法;
第二类,从甲地不经过乙地到丙地,共有3种走法.
根据分类加法计数原理,不同走法的种数是
N=8+3=11 种在A、B两区域内可以选择0~9内的任意整数,当A区域内的数比B区域内的数大时,共有多少种结果?利用分类计数原理解决问题: 第一类,A区域的数字为1,B区域上的数字有1种选法;
第二类,A区域的数字为2,B区域上的数字有2种选法;
第三类,A区域的数字为3,B区域上的数字有3种选法;
……
第九类,A区域的数字为9,B区域的数字有9种选法.
根据分类相加计数原理,A区域内的数比B区域内的数大的有
1+2+3+……+9=45种结果.
利用对称性解决问题:………… 共有100种情况,其中有10种是相同的,
100-10=90, A区域比B区域大的共有 90÷2=45种结果.利用坐标法解决问题:x<yx>yx大于y的部分共有45个整数点,所有A区域比B区域大的两位数共有45种结果如图所示,A、B、C、D四个区域,用红、黄、蓝三种颜色涂色,要求任意两个相邻区域的颜色各不相同,共有多少种不同的涂法?可以分为两类方案:
第一类方案:共用三种颜色去涂色
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;第三步,C区域选择一个颜色,有2种选择;第四步,D区域选择一个颜色,有1种选择.
第一类方案中,共有 3×2×2×1=12种方法.
第二类方案:共用了两种颜色去涂色
第一步,A区域选择一个颜色,有3种选择;第二步,B区域选择一个颜色,有2种选择;第三步,C区域与A区域选择颜色相同;
第四步,D区域与B区域选择相同.
第二类方案中,共有3×2×1×1=6种方法.
则共有12+6=18种方法ABCD方法一:如图所示,A、B、C、D四个区域,用红、黄、蓝三种颜色涂色,要求任意两个相邻区域的颜色各不相同,共有多少种不同的涂法?ABCD可以分为两类方案:
第一类方案:若A、C涂色相同
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;
第三步,C区域与A区域选择相同,有1种选择;
第四步,D区域选择一个颜色,有2种选择.
第一类方案中,共有 3×2×1×2=12种方法.
第二类方案:若A、C涂色不相同
第一步,A区域选择一个颜色,有3种选择;
第二步,B区域选择一个颜色,有2种选择;
第三步,C区域选择一个颜色且与A颜色不同 ,有1种选择;
第四步,D区域选择一个颜色,有1种选择.
第二类方案中,共有3×2×1×1=6种方法.
则共有12+6=18种方法方法二: 在运用排列、组合方法时,经常要用到分类加法计数原理与分步乘法计数原理. 这节课,就是排列、组合方法的一个基础. 两个定义:分类加法计数原理、分步 乘法计数原理
三个思想:转化与化归、类比思想、 数形结合解答计数原理问题的一般思维过程:作业:
教材p12 1、2描述分类计数原理和分步计数原理的诗:●两大原理妙无穷
●解题应用各不同
●多思缜密最重要
●茫茫数理此中求再 见敬请指导.
