1.1 分类加法计数原理与分步乘法计数原理(一) 课件(24张PPT)
文档属性
| 名称 | 1.1 分类加法计数原理与分步乘法计数原理(一) 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 123.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 12:21:46 | ||
图片预览






文档简介
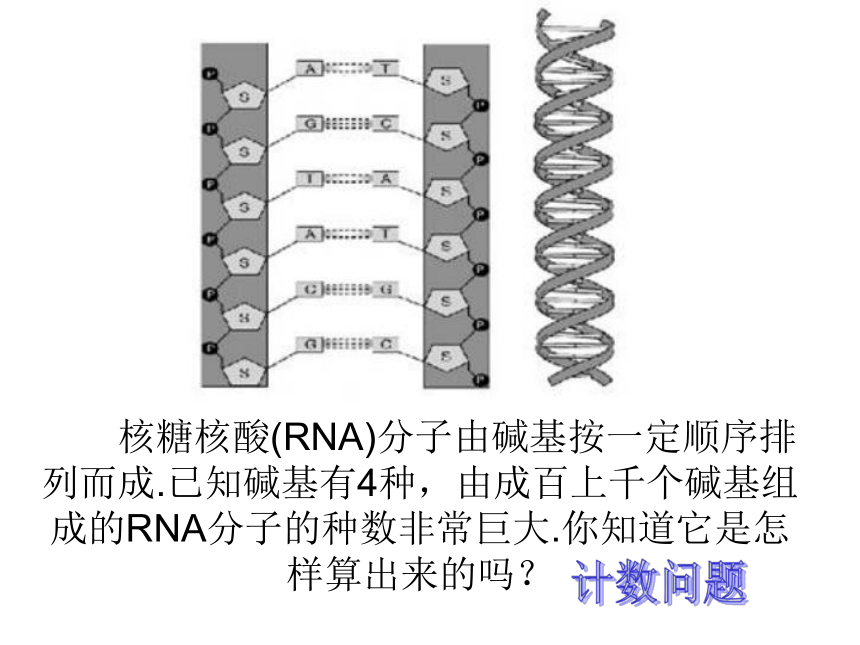
课件24张PPT。分类加法计数原理与 分步乘法计数原理 (第一课时) 2011年9月29日天宫一号成功发射,此次有4种濒临灭绝的植物种子搭载“天宫一号”进入太空,希望令种子产生基因变异.大哉,数学之为用!
从火箭之速,到粒子之微,无处不用数学。 核糖核酸(RNA)分子由碱基按一定顺序排列而成.已知碱基有4种,由成百上千个碱基组成的RNA分子的种数非常巨大.你知道它是怎样算出来的吗?计数问题 在计算机中的字符由二进制表示,英文字母和汉字所需的字节数不一样.你知道为什么吗? 问题1 汉字在计算机的机器语言中是用16位的数字表示(0或1),你如何“数出”16位数字最多可以表示多少个不同的汉字? 计数问题问题2 (自主探究)尝试完成下列计数问题,并从数学的角度对这些问题进行分类,试说明分类的依据. 看学案问题2,
完成表一和表二 (1)(4)(5):完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法. 那么完成这件事共有N=m+n种不同的方法. 叫做:分类加法计数原理 (2)(3)(6):完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法. 那么完成这件事共有N=m×n 种不同的方法.
叫做:分步乘法计数原理 探究归纳分析:(1)明确目标:要完成一件什么事情?
(2)如何完成?分类
(3)如何列式?加法解:这名同学可以任取一个专业,在A、B两所大学中只能选择一所,在A大学中有5种专业选择方法,在B大学中有4种专业选择方法.又由于没有一个强项专业是两所大学共有的,因此根据分类计数原理:这名同学可能的专业选择共有5+4=9种例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学 B大学
化学 会计学
医学 信息技术学
物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择呢? 生物学 数学
思考: 若还有C大学,其中强项专业为:新闻学、金融学、人力资源学.那么,他共有多少种选择呢?注意:类别增加,且专业各不相同.——分类加法计数原理的一般形式思考2:某班级组织了三个研究性学习小组,已知数理组20人,科技组15人,人文组12人,现从班级中选出一人担任班长,你认为总共有多少种不同的选法?请各抒己见.分类的要求——“不重不漏” 例2 要从甲、乙、丙、丁4幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?解:从4幅画中选出2幅挂在左、右两边墙上,可以分两个步骤完成:第1步,从4幅画中选1幅挂在左边墙上,有4种选法;第2步,从剩下的3幅画中选1幅挂在右边墙上,有3种选法.根据分步乘法计数原理,不同挂法的种数是 N=4×3=1212种挂法可以表示如下:例2 要从甲、乙、丙、丁4幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?思考 若还需要再选1幅画挂在在前面墙上的指定位置,共有多少种不同的挂法?N=4 × 3 × 2=24分步乘法计数原理的一般形式例3 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. ①从书架上任取1本书,有多少种不同的取法? ②从书架的第1、2、3层各取1本书,有多少种不同的取法?分析:
(1)要完成哪一件事?——“任取一本”与“各取一本”(2)如何完成这件事?——“分类”还是“分步”(3)如何列式?有一即可不可兼取缺一不可必须同取区别1“分类”问题,相加“分步”问题,相乘区别2
有一即可,不能兼取:每类办法都能独立完成这件事情.直达目标.缺一不可,必须同取:每一步得到的只是中间结果,任何一步都不能能独立完成这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情. 中转完成.例3 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. ①从书架上任取1本书,有多少种不同的取法? ②从书架的第1、2、3层各取1本书,有多少种不同的取法?③从书架上任取两本不同学科的书,有多少种不同的取法?N1=4×3=12N2=4×2=8N3=6×2=6N= N1+N2 +N3=26 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =14 巩固练习 创新设计
请根据今天所学习的原理,以四人小组为单位, 设计一个运用两个计数原理的计数问题.创新设计
请根据今天所学习的原理,以四人小组为单位,设计一个运用两个计数原理的计数问题.解决问题1 汉字在计算机的机器语言中是用16位的数字表示(0或1),你如何“数出”16位数字共能表示多少个不同的汉字? 延伸阅读 常用汉字数量大约是2500到7000之间,根据统计:毛泽东所有的著作仅含3136个不同的汉字. 知识方法思想分类加法计数原理;
分步乘法计数原理.归纳与类比;
分类法、分步法.特殊到一般;化归转化.小结升华 知识感悟 计数原理入门径, 何时相加何时乘? 分类相加无重漏, 分步相乘步骤整。课后作业 1.书面作业:课本习题1.1A组第1,3,4题.
2.阅读作业:课本P11-12 研究与发现“子集的个数有多少”.
3.弹性作业:编一道运用分类加法计数原理和分步乘法计数原理解答的应用题,并加以解答.
从火箭之速,到粒子之微,无处不用数学。 核糖核酸(RNA)分子由碱基按一定顺序排列而成.已知碱基有4种,由成百上千个碱基组成的RNA分子的种数非常巨大.你知道它是怎样算出来的吗?计数问题 在计算机中的字符由二进制表示,英文字母和汉字所需的字节数不一样.你知道为什么吗? 问题1 汉字在计算机的机器语言中是用16位的数字表示(0或1),你如何“数出”16位数字最多可以表示多少个不同的汉字? 计数问题问题2 (自主探究)尝试完成下列计数问题,并从数学的角度对这些问题进行分类,试说明分类的依据. 看学案问题2,
完成表一和表二 (1)(4)(5):完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法. 那么完成这件事共有N=m+n种不同的方法. 叫做:分类加法计数原理 (2)(3)(6):完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法. 那么完成这件事共有N=m×n 种不同的方法.
叫做:分步乘法计数原理 探究归纳分析:(1)明确目标:要完成一件什么事情?
(2)如何完成?分类
(3)如何列式?加法解:这名同学可以任取一个专业,在A、B两所大学中只能选择一所,在A大学中有5种专业选择方法,在B大学中有4种专业选择方法.又由于没有一个强项专业是两所大学共有的,因此根据分类计数原理:这名同学可能的专业选择共有5+4=9种例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学 B大学
化学 会计学
医学 信息技术学
物理学 法学
工程学
如果这名同学只能选一个专业,那么他共有多少种选择呢? 生物学 数学
思考: 若还有C大学,其中强项专业为:新闻学、金融学、人力资源学.那么,他共有多少种选择呢?注意:类别增加,且专业各不相同.——分类加法计数原理的一般形式思考2:某班级组织了三个研究性学习小组,已知数理组20人,科技组15人,人文组12人,现从班级中选出一人担任班长,你认为总共有多少种不同的选法?请各抒己见.分类的要求——“不重不漏” 例2 要从甲、乙、丙、丁4幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?解:从4幅画中选出2幅挂在左、右两边墙上,可以分两个步骤完成:第1步,从4幅画中选1幅挂在左边墙上,有4种选法;第2步,从剩下的3幅画中选1幅挂在右边墙上,有3种选法.根据分步乘法计数原理,不同挂法的种数是 N=4×3=1212种挂法可以表示如下:例2 要从甲、乙、丙、丁4幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?思考 若还需要再选1幅画挂在在前面墙上的指定位置,共有多少种不同的挂法?N=4 × 3 × 2=24分步乘法计数原理的一般形式例3 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. ①从书架上任取1本书,有多少种不同的取法? ②从书架的第1、2、3层各取1本书,有多少种不同的取法?分析:
(1)要完成哪一件事?——“任取一本”与“各取一本”(2)如何完成这件事?——“分类”还是“分步”(3)如何列式?有一即可不可兼取缺一不可必须同取区别1“分类”问题,相加“分步”问题,相乘区别2
有一即可,不能兼取:每类办法都能独立完成这件事情.直达目标.缺一不可,必须同取:每一步得到的只是中间结果,任何一步都不能能独立完成这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情. 中转完成.例3 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. ①从书架上任取1本书,有多少种不同的取法? ②从书架的第1、2、3层各取1本书,有多少种不同的取法?③从书架上任取两本不同学科的书,有多少种不同的取法?N1=4×3=12N2=4×2=8N3=6×2=6N= N1+N2 +N3=26 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =14 巩固练习 创新设计
请根据今天所学习的原理,以四人小组为单位, 设计一个运用两个计数原理的计数问题.创新设计
请根据今天所学习的原理,以四人小组为单位,设计一个运用两个计数原理的计数问题.解决问题1 汉字在计算机的机器语言中是用16位的数字表示(0或1),你如何“数出”16位数字共能表示多少个不同的汉字? 延伸阅读 常用汉字数量大约是2500到7000之间,根据统计:毛泽东所有的著作仅含3136个不同的汉字. 知识方法思想分类加法计数原理;
分步乘法计数原理.归纳与类比;
分类法、分步法.特殊到一般;化归转化.小结升华 知识感悟 计数原理入门径, 何时相加何时乘? 分类相加无重漏, 分步相乘步骤整。课后作业 1.书面作业:课本习题1.1A组第1,3,4题.
2.阅读作业:课本P11-12 研究与发现“子集的个数有多少”.
3.弹性作业:编一道运用分类加法计数原理和分步乘法计数原理解答的应用题,并加以解答.
