1.3.2 “杨辉三角”与二项式系数的性质 课件(18张PPT)
文档属性
| 名称 | 1.3.2 “杨辉三角”与二项式系数的性质 课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 12:08:42 | ||
图片预览



文档简介
课件18张PPT。1.3.2“杨辉三角”
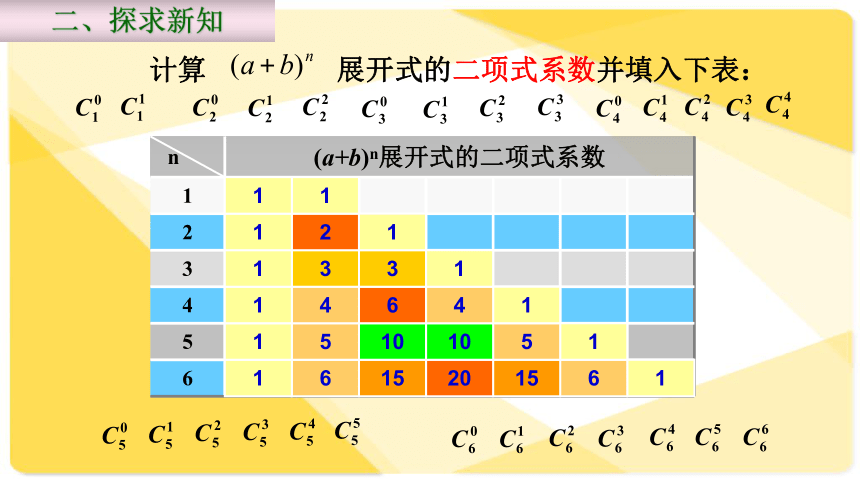
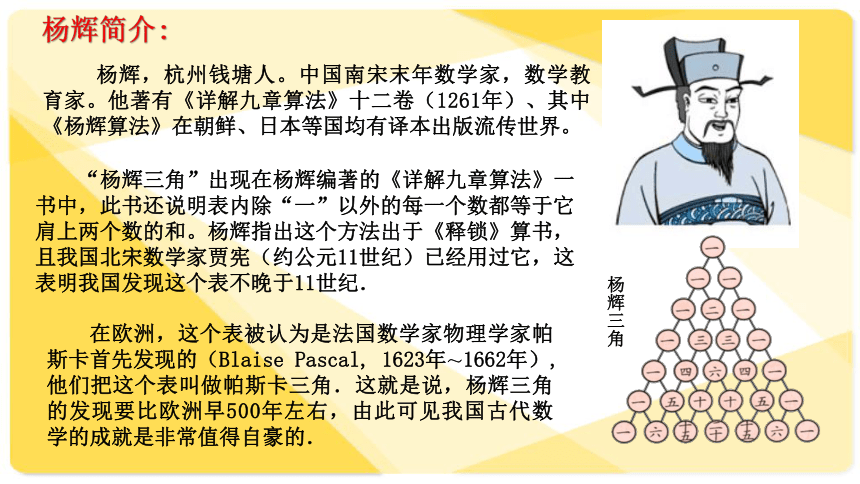
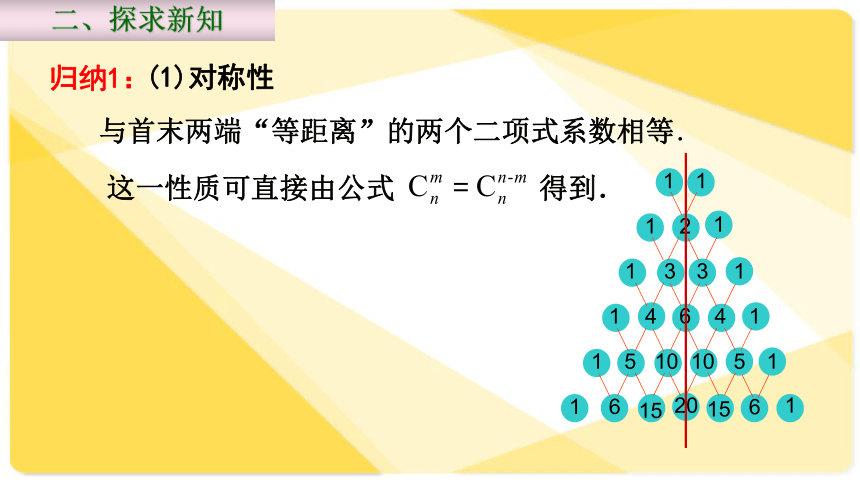
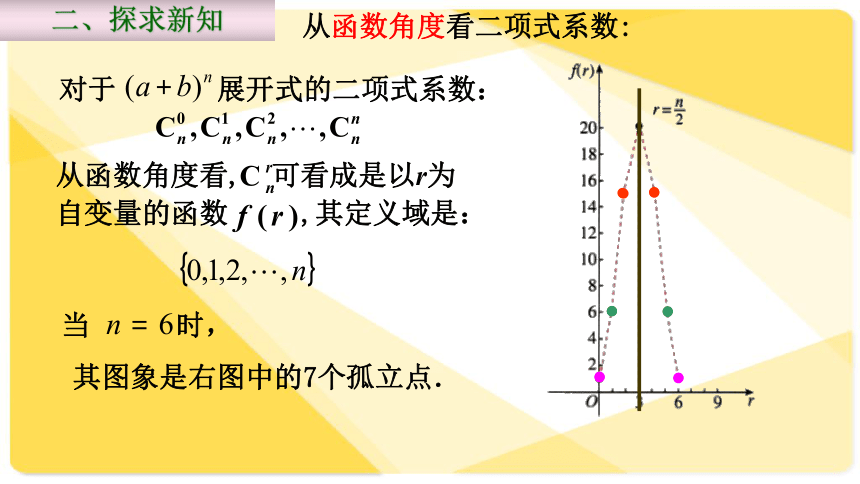
与二项式系数的性质人民教育出版社数学选修2-3 二项式定理:二项展开式中的二项式系数指的是那些?展开式的第 项为:一般地,对于 有一、复习回顾计算 展开式的二项式系数并填入下表:二、探求新知 杨辉,杭州钱塘人。中国南宋末年数学家,数学教育家。他著有《详解九章算法》十二卷(1261年)、其中《杨辉算法》在朝鲜、日本等国均有译本出版流传世界。杨辉简介: 在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的(Blaise Pascal, 1623年~1662年),他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得自豪的. “杨辉三角”出现在杨辉编著的《详解九章算法》一书中,此书还说明表内除“一”以外的每一个数都等于它肩上两个数的和。杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪.杨辉三角思考1:请看系数有没有明显的规律?(1)每行的数有什么特点?(2)上下两行有什么关系吗? (3)根据这两条规律,大家能写出下面的二项式系数吗?(2)在相邻两行中,除1以外的每一个数都等于它“肩上”两数的和,即:(1)在同一行中,每行两端都是1,与这两个1等距离的项的系数相等,即:二、探求新知(1)对称性 与首末两端“等距离”的两个二项式系数相等.这一性质可直接由公式 得到.二、探求新知归纳1:对于 展开式的二项式系数: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,二、探求新知从函数角度看二项式系数:其图象是右图中的7个孤立点.思考2:结合杨辉三角形和对应函数图像,二项式系数是怎么变化的,单调性是怎样的?二、探求新知在同一行中,每行的数都是先增后减的!(2)增减性与最大值 二、探求新知思考3:观察杨辉三角形,各行的数的和为多少?246416832……第5行 1 5 10 10 5 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第8行 1 8 28 56 70 56 28 8 1第n行……三、知识升华奇数项数字的和与所有偶数项数字的和呢?二、探求新知-2-109410933. 已知
则 方法——赋值法.杨辉三角的其它规律四、思维拓展:“杨辉三角”中的一些秘密第6行 1 6 15 6 1第7行 1 7 21 21 7 1课外探索1:由下面各式的和,探索其规律四、思维拓展:“杨辉三角”中的一些秘密 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……138132134第8行 1 8 28 56 70 56 28 8 1这就是著名的斐波那契数列 课外探索2:写出斜线上各行数字的和,有什么规律?四、思维拓展:“杨辉三角”中的一些秘密斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。斐波那契数列以如下被以递归的方法定义:斐波纳契数列的通项公式: 在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果自然界中动物的繁殖、植物的生长规律都遵循斐波拉契数列这一规律。四、思维拓展:“杨辉三角”中的一些秘密四、思维拓展:“杨辉三角”中的一些秘密五、当堂小结2.利用杨辉三角和函数图像可得二项式系数的对称性,增减性和最大值; 3.常用赋值法解决二项式系数有关问题;4.课外探索:通过观察找出杨辉三角每行数据间的相互关系,发现更多隐藏在杨辉三角里的秘密,得出更多关于二项式定理系数的性质!1.当 时,常用杨辉三角处理二项式系数的问题;谢谢指导!
与二项式系数的性质人民教育出版社数学选修2-3 二项式定理:二项展开式中的二项式系数指的是那些?展开式的第 项为:一般地,对于 有一、复习回顾计算 展开式的二项式系数并填入下表:二、探求新知 杨辉,杭州钱塘人。中国南宋末年数学家,数学教育家。他著有《详解九章算法》十二卷(1261年)、其中《杨辉算法》在朝鲜、日本等国均有译本出版流传世界。杨辉简介: 在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的(Blaise Pascal, 1623年~1662年),他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得自豪的. “杨辉三角”出现在杨辉编著的《详解九章算法》一书中,此书还说明表内除“一”以外的每一个数都等于它肩上两个数的和。杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪.杨辉三角思考1:请看系数有没有明显的规律?(1)每行的数有什么特点?(2)上下两行有什么关系吗? (3)根据这两条规律,大家能写出下面的二项式系数吗?(2)在相邻两行中,除1以外的每一个数都等于它“肩上”两数的和,即:(1)在同一行中,每行两端都是1,与这两个1等距离的项的系数相等,即:二、探求新知(1)对称性 与首末两端“等距离”的两个二项式系数相等.这一性质可直接由公式 得到.二、探求新知归纳1:对于 展开式的二项式系数: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,二、探求新知从函数角度看二项式系数:其图象是右图中的7个孤立点.思考2:结合杨辉三角形和对应函数图像,二项式系数是怎么变化的,单调性是怎样的?二、探求新知在同一行中,每行的数都是先增后减的!(2)增减性与最大值 二、探求新知思考3:观察杨辉三角形,各行的数的和为多少?246416832……第5行 1 5 10 10 5 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第8行 1 8 28 56 70 56 28 8 1第n行……三、知识升华奇数项数字的和与所有偶数项数字的和呢?二、探求新知-2-109410933. 已知
则 方法——赋值法.杨辉三角的其它规律四、思维拓展:“杨辉三角”中的一些秘密第6行 1 6 15 6 1第7行 1 7 21 21 7 1课外探索1:由下面各式的和,探索其规律四、思维拓展:“杨辉三角”中的一些秘密 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……138132134第8行 1 8 28 56 70 56 28 8 1这就是著名的斐波那契数列 课外探索2:写出斜线上各行数字的和,有什么规律?四、思维拓展:“杨辉三角”中的一些秘密斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。斐波那契数列以如下被以递归的方法定义:斐波纳契数列的通项公式: 在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果自然界中动物的繁殖、植物的生长规律都遵循斐波拉契数列这一规律。四、思维拓展:“杨辉三角”中的一些秘密四、思维拓展:“杨辉三角”中的一些秘密五、当堂小结2.利用杨辉三角和函数图像可得二项式系数的对称性,增减性和最大值; 3.常用赋值法解决二项式系数有关问题;4.课外探索:通过观察找出杨辉三角每行数据间的相互关系,发现更多隐藏在杨辉三角里的秘密,得出更多关于二项式定理系数的性质!1.当 时,常用杨辉三角处理二项式系数的问题;谢谢指导!
