2.4 正态分布 课件26张PPT
文档属性
| 名称 | 2.4 正态分布 课件26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 12:18:02 | ||
图片预览





文档简介
课件26张PPT。2.4 正态分布教学目标:
1.?知识目标:
理解并掌握(标准)正态分布和正态曲线的概念、意义及性质,并能简单应用。
2.能力目标:
能用正态分布、正态曲线研究有关随机变量分布的规律,引导学生通过观察并探究规律,提高分析问题,解决问题的能力;培养学生数形结合,函数与
方程等数学思想方法。
3.?情感目标:
通过教学中一系列的探究过程使学生体验发现的快乐,形成积极的情感,培养学生的进取意识和科学精神。授课人:昂 冉 在实际遇到的许多随机现象都服从或近似服从正态分布:在生产中,在正常生产条件下各种产品的质量指标; 在测量中,测量结果; 在生物学中,同一群体的某一特征;……; 在气象中,某地每年七月份的平均气温、平均湿度
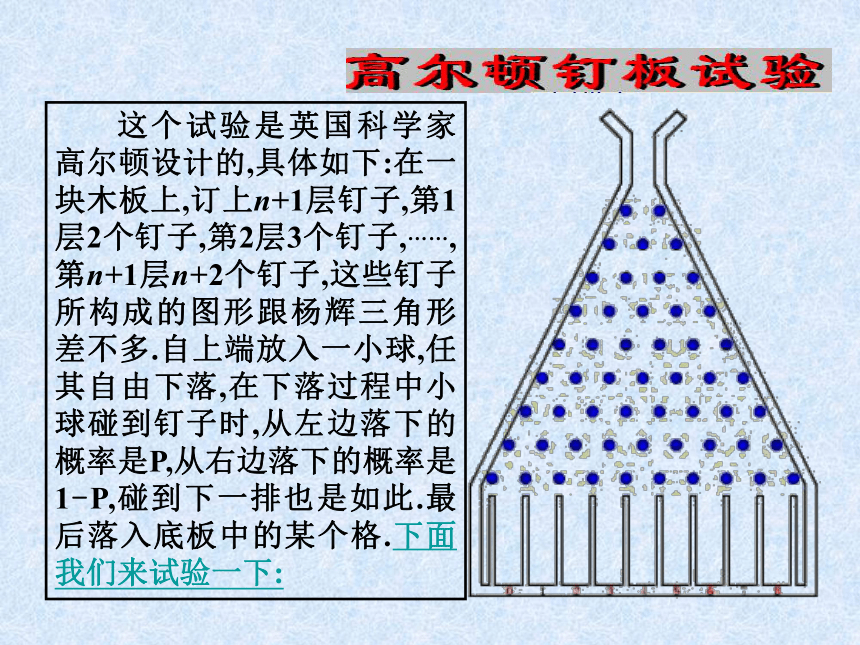
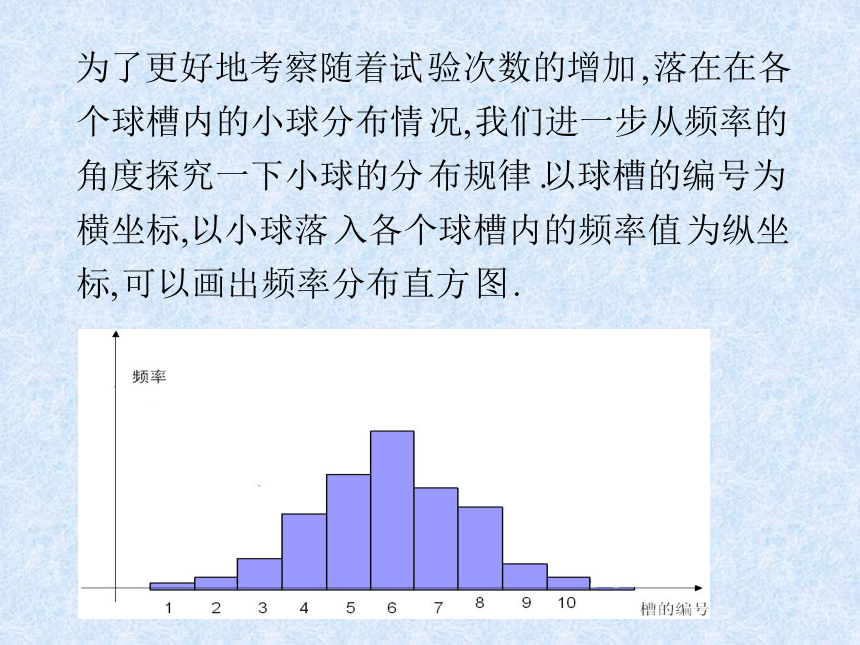
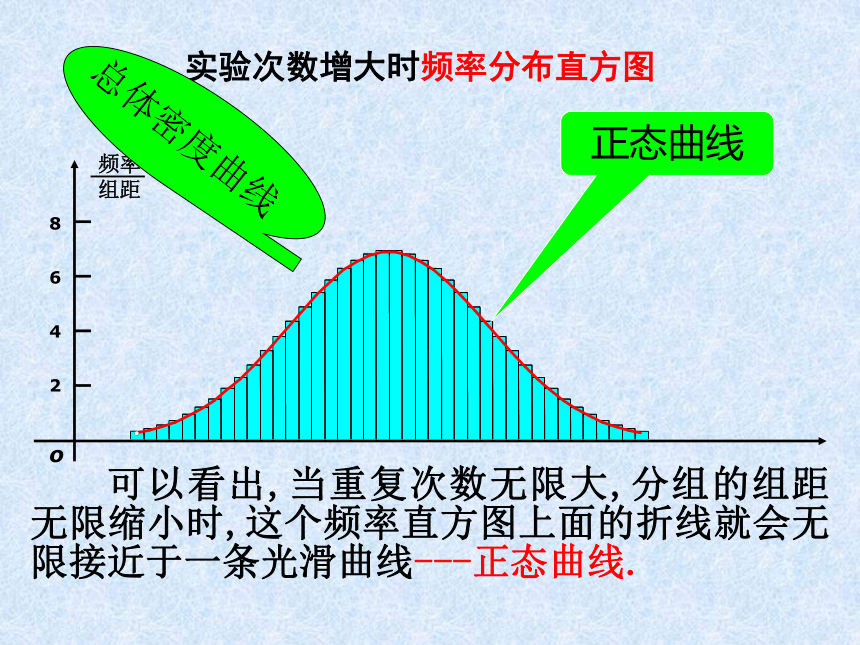
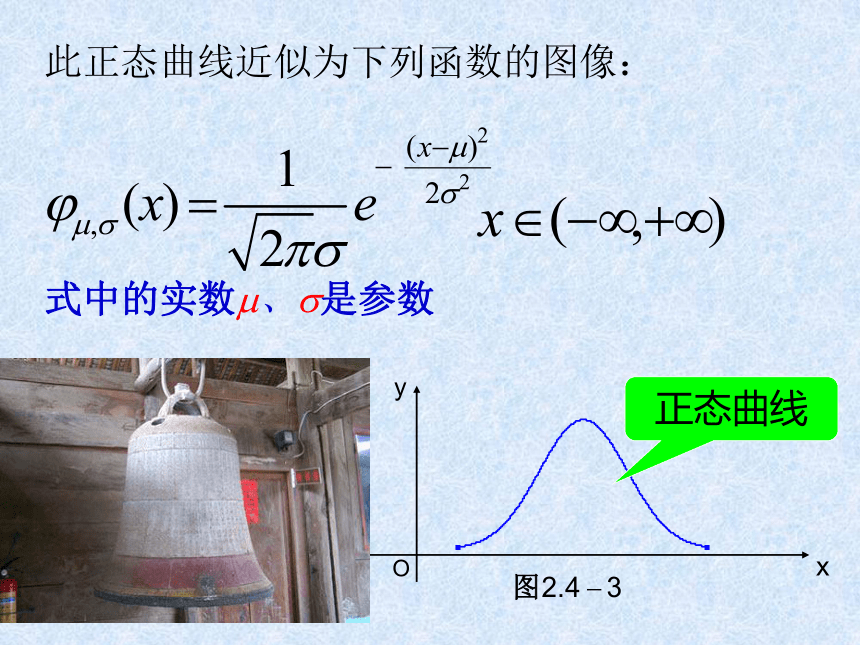
以及降雨量等,水文中的水位; 总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。正态分布在概率和统计中占有重要地位。 这个试验是英国科学家高尔顿设计的,具体如下:在一块木板上,订上n+1层钉子,第1层2个钉子,第2层3个钉子,……,第n+1层n+2个钉子,这些钉子所构成的图形跟杨辉三角形差不多.自上端放入一小球,任其自由下落,在下落过程中小球碰到钉子时,从左边落下的概率是P,从右边落下的概率是1-P,碰到下一排也是如此.最后落入底板中的某个格.下面我们来试验一下:o2468实验次数增大时频率分布直方图正态曲线 可以看出,当重复次数无限大,分组的组距无限缩小时,这个频率直方图上面的折线就会无限接近于一条光滑曲线---正态曲线.正态曲线此正态曲线近似为下列函数的图像:式中的实数m、s是参数 若用X表示落下的小球第1次与高尔顿板底部接触时的坐标,则X是一个随机变量.X落在区间(a,b]的概率为:则称X 的分布为正态分布. 正态分布由参数m、s唯一确定, m、s分别表示总体的平均数与标准差.正态分布记作N( m,s2).其图象称为正态曲线.1.正态分布定义xy0 a b如果对于任何实数
a
A.
B.
C.
D.B练一练正态密度函数表示式当μ= 0,σ=1时标准正态密度函数表示式2.正态曲线的性质具有两头低、中间高、左右对称的基本特征(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 2、正态曲线的性质(4)曲线与x轴之间的面积为1(3)曲线在x=μ处达到峰值(最高点)σ=0.5μ= -1μ=0 μ= 1 (5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移。2、正态曲线的性质??=1μ=0 (6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.2、正态曲线的性质练一练 设两个正态分布N(μ1,σ1)(σ1>0)和
N(μ2,σ2)(σ2>0)的密度函数图象如图所
示,则有( )A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1>σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2A特别有(熟记)3. 3σ原则 由于这些概率值很小(一般不超过5 % ),通常称这些情况发生为小概率事件。 正态总体在 以外取值的概率只有0.0026.操作应用,巩固新知例1、(1)在某次数学考试中,考生的X ~N(90,100).
考试成绩X位于区间(70,110)上的概率是
(2)设连续型随机变量X~N(0,1),则 = , = . 0.50.95440.9544例2、若X~N(5,1),求P(6 P(4 所以P(3 =0.9544-0.6826=0.2718,
由对称性得P(3所以P(62.已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228D练习:1.设连续型随机变量X~N(μ, σ2),则 = , 0.5归纳小结1.正态曲线及其特点;
2.正态分布及概率计算;
3.3s原则。作
业第75页习题2.4的A组1,B组2;
课外思考.请尝试从解析式角度分析正态曲线的对称性与最值。正态分布B:在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 ,已知成绩在90分以上(含90分)的学生有12名。试问此次参赛的学生总数约有多少人?
1.?知识目标:
理解并掌握(标准)正态分布和正态曲线的概念、意义及性质,并能简单应用。
2.能力目标:
能用正态分布、正态曲线研究有关随机变量分布的规律,引导学生通过观察并探究规律,提高分析问题,解决问题的能力;培养学生数形结合,函数与
方程等数学思想方法。
3.?情感目标:
通过教学中一系列的探究过程使学生体验发现的快乐,形成积极的情感,培养学生的进取意识和科学精神。授课人:昂 冉 在实际遇到的许多随机现象都服从或近似服从正态分布:在生产中,在正常生产条件下各种产品的质量指标; 在测量中,测量结果; 在生物学中,同一群体的某一特征;……; 在气象中,某地每年七月份的平均气温、平均湿度
以及降雨量等,水文中的水位; 总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。正态分布在概率和统计中占有重要地位。 这个试验是英国科学家高尔顿设计的,具体如下:在一块木板上,订上n+1层钉子,第1层2个钉子,第2层3个钉子,……,第n+1层n+2个钉子,这些钉子所构成的图形跟杨辉三角形差不多.自上端放入一小球,任其自由下落,在下落过程中小球碰到钉子时,从左边落下的概率是P,从右边落下的概率是1-P,碰到下一排也是如此.最后落入底板中的某个格.下面我们来试验一下:o2468实验次数增大时频率分布直方图正态曲线 可以看出,当重复次数无限大,分组的组距无限缩小时,这个频率直方图上面的折线就会无限接近于一条光滑曲线---正态曲线.正态曲线此正态曲线近似为下列函数的图像:式中的实数m、s是参数 若用X表示落下的小球第1次与高尔顿板底部接触时的坐标,则X是一个随机变量.X落在区间(a,b]的概率为:则称X 的分布为正态分布. 正态分布由参数m、s唯一确定, m、s分别表示总体的平均数与标准差.正态分布记作N( m,s2).其图象称为正态曲线.1.正态分布定义xy0 a b如果对于任何实数
a
A.
B.
C.
D.B练一练正态密度函数表示式当μ= 0,σ=1时标准正态密度函数表示式2.正态曲线的性质具有两头低、中间高、左右对称的基本特征(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 2、正态曲线的性质(4)曲线与x轴之间的面积为1(3)曲线在x=μ处达到峰值(最高点)σ=0.5μ= -1μ=0 μ= 1 (5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移。2、正态曲线的性质??=1μ=0 (6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.2、正态曲线的性质练一练 设两个正态分布N(μ1,σ1)(σ1>0)和
N(μ2,σ2)(σ2>0)的密度函数图象如图所
示,则有( )A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1>σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2A特别有(熟记)3. 3σ原则 由于这些概率值很小(一般不超过5 % ),通常称这些情况发生为小概率事件。 正态总体在 以外取值的概率只有0.0026.操作应用,巩固新知例1、(1)在某次数学考试中,考生的X ~N(90,100).
考试成绩X位于区间(70,110)上的概率是
(2)设连续型随机变量X~N(0,1),则 = , = . 0.50.95440.9544例2、若X~N(5,1),求P(6
由对称性得P(3
A.0.9544 B.0.0456 C.0.9772 D.0.0228D练习:1.设连续型随机变量X~N(μ, σ2),则 = , 0.5归纳小结1.正态曲线及其特点;
2.正态分布及概率计算;
3.3s原则。作
业第75页习题2.4的A组1,B组2;
课外思考.请尝试从解析式角度分析正态曲线的对称性与最值。正态分布B:在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 ,已知成绩在90分以上(含90分)的学生有12名。试问此次参赛的学生总数约有多少人?
