选修2-3 第二章 随机变量及其分布 统计与概率复习课件 27张PPT
文档属性
| 名称 | 选修2-3 第二章 随机变量及其分布 统计与概率复习课件 27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 12:22:38 | ||
图片预览





文档简介
课件27张PPT。课程改革永无止境,
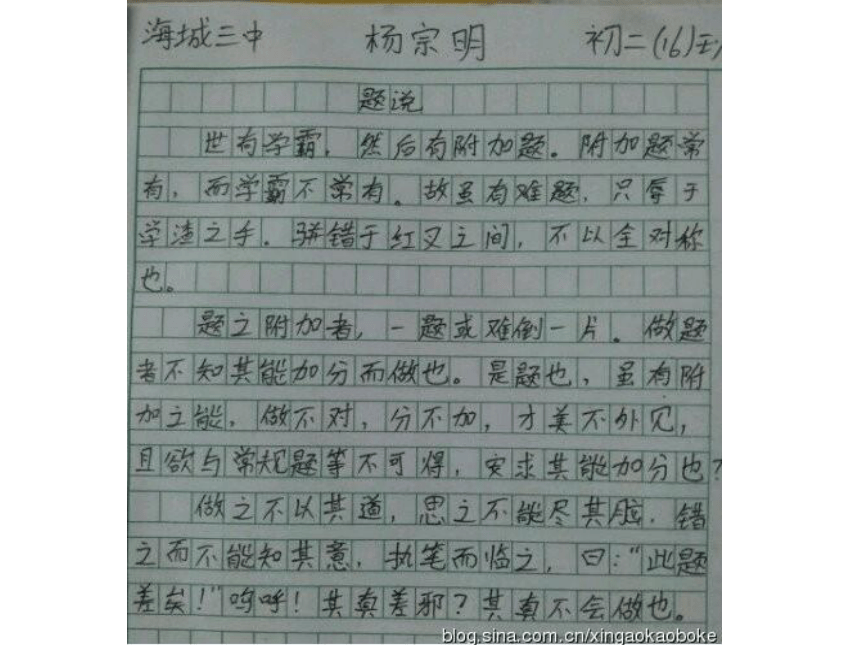
对高中数学教学的认识和探讨永远在路上 复习:统计与概率高中数学《题说》 ……
做之不能以其道,思之不能尽其法,错之而不能知其意,执笔而临之,曰:“此题难矣!”呜呼!其真难邪?其真不会做也。从总体中
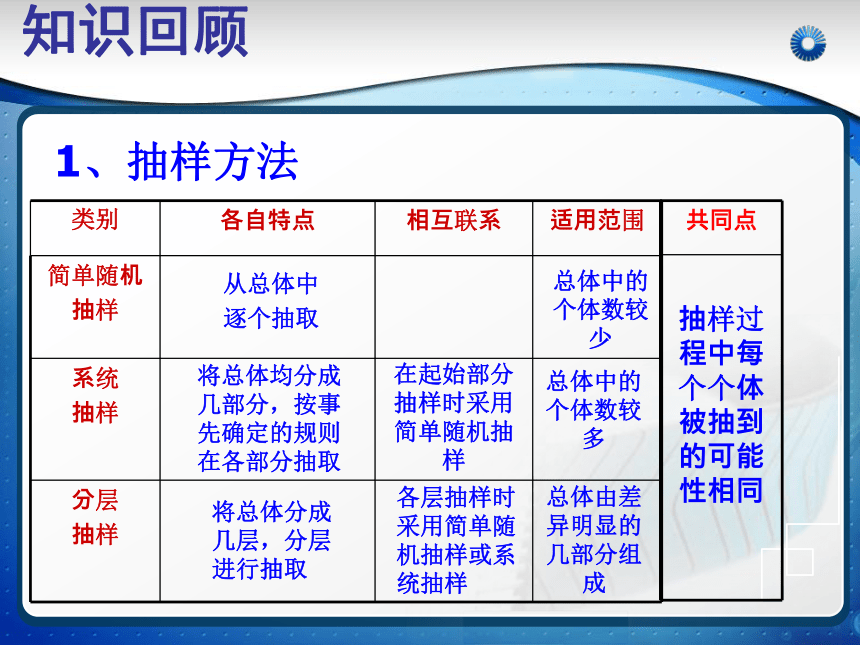
逐个抽取将总体均分成几部分,按事先确定的规则在各部分抽取将总体分成几层,分层进行抽取在起始部分抽样时采用简单随机抽样各层抽样时采用简单随机抽样或系统抽样总体中的个体数较少总体中的个体数较多1、抽样方法总体由差异明显的几部分组成知识回顾 一般地,作频率分布直方图的步骤如下:(1)求极差。(2)决定组数和组距。
(3)分组。 (4)列出频率分布表;
(5)画出频率分布直方图(纵轴表示频率/组距).2、总体分布的估计知识回顾3、总体特征数的估计设一组样本数据 ,众数、中位数、
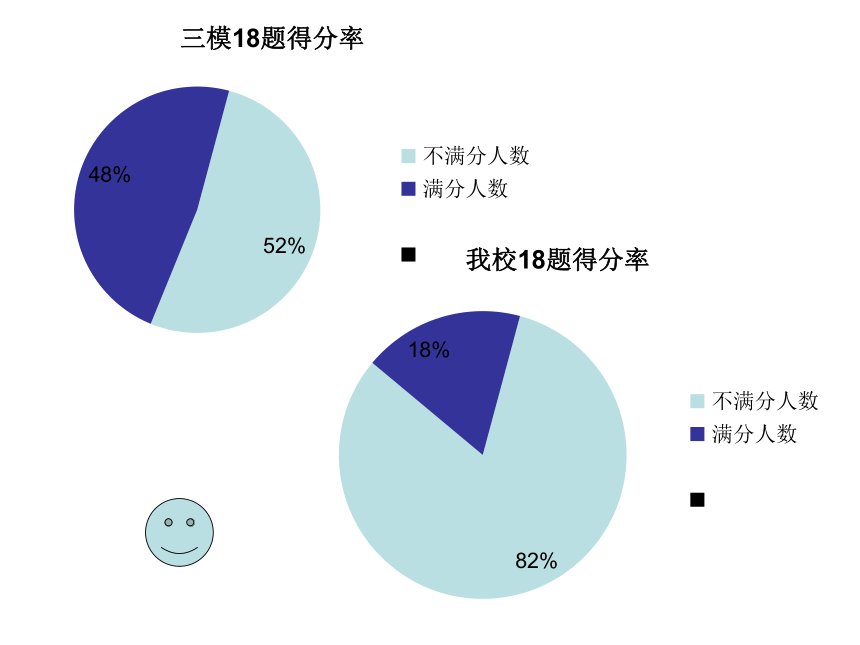
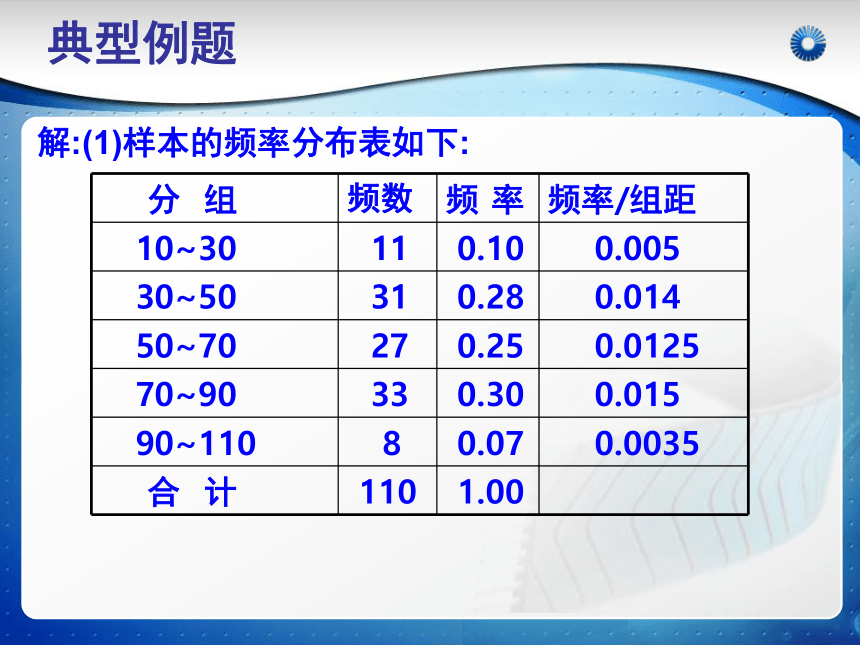
平均数、方差、标准差例:本次三模,数学有效试卷共116份,除去其他科未答满者3人,为便 于计算,再随机剔除3人,成绩分组以及各组的频 数如下:
[10,30),11; [30,50),31;
[50,70),27; [70,90),33; [90,110),8;
(1)列出样本的频率分布表
(2)画出频率分布直方图
(3)根据频率分布直方图求众数、中位数、平均数、方差
典型例题解:(1)样本的频率分布表如下:典型例题(2)频率分布直方图:典型例题(2)频率分布直方图:典型例题1:求某一组频率时,其中有两个组以上的纵坐标相等。
2:纵坐标为频率比组距,易与频 率混淆。
3:分层抽样时,人数易错。
频率分布直方图多出现在大题第一问, 是做概率的基础数据,一错全错!
总结易错处:独立性检验例:以三模与二模本班成绩做对比,问是否有90%的把握认为学习成绩上升与学习时间超过晚上12点有关?高考考查重点:
1、相互独立事件的概率.
2、n次独立重复试验的模型及二项分布.
辨析:
互斥事件、对立事件、相互独立事件相互独立与二项分布复习(1)独立重复试验
在相同条件下可重复进行的,各次之间相互独立的一种试验,在这种试验中每一次试验只有____结果,即要么发生,要么不发生,且任何一次试验中发生的概率都是______的.
(2)二项分布 进行n次试验,如果满足以下条件:
①每次试验只有两个相互独立的结果,
②“成功”的概率均为p,“失败”的概率均为1-p;
2.独立重复试验与二项分布两种一样③各次试验是相互独立的.
(1)设X为大黄在途中遇到红灯的次数,求X的分布列;
(2)设Y为大黄在首次停下来前经过的路口数,求Y的分布列;
(3)求大黄在途中至少遇到一次红灯的概率.
(2)由于Y表示这名学生在首次停车时经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5,6.
其中:{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.超几何分布与二项分布的区别和联系
① 超几何分布定义:一批产品共N件,其中有M件次品,随机取出的n件产品中,次品数x服从超几何分布,
超几何分布满足两个条件:一是抽取的产品不再放回,二是总产品数量N较小。
②二项分布定义:在n次独立重复试验中,每次试验A发生的概率均为p,那么在n次独立重复试验中,事件A恰好发生k次的概率,
则称X服从二项分布,记为X~B(n,p)
二项分布也满足两个条件:一是有放回、独立重复;二是恰好发生k次。
③当抽取的方式从无放回变为有放回或者总产品数量N很大时,超几何分布变为二项分布 .例:长时间用手机上网严重影响学生健康与学习,如果学生平均每周手机的时长超过30个小时,则被称为网瘾少年,为了解高三学生的手机上网情况,经统计,四班30人中有10人一周上网超过30小时,五班20人中有10人一周上网超过30小时。
(1)从四班的样本数据中抽取4人,求恰有1人是网瘾少年的概率
(2)从五班的样本中随机抽取4人,记网瘾少年人数为X,写出其分布列和数学期望(1)混淆“互斥”与“对立”、“互斥”与
“独立”而致误
(2)混淆“条件概率”与“相互独立事件的概
率”而致误
(3)混淆“二项分布”与“超几何分布”而致误
(4)忽视正态分布的图像而致误
(5)线性回归方程的性质不熟练而致误
(6)不理解独立性检验的思想而致误 统计与概率教学总结统计与概率教学总结 (1)注重培养学生阅读理解能力;
(2)注重提升学生数学建模能力;
(3)注重培养学生处理数据能力;
(4)注重提高学生准确运算能力。统计与概率教学总结 (1)对照考纲复习课本?吃透基本定义定理
(2)按照“知识-题型-方法-思想”构建知识
体系
(3)数学思想方法:函数、方程、数形结合、
分类讨论
(4)找错题原因更重要,试卷关键字作记号统计与概率教学总结正态分布下节任务单几何概型回归方程复习思路1、对照考纲复习课本?吃透基本定义定理2、按照“知识-题型-方法-思想”构建知识体系 3、数学思想方法:函数、方程、数形结合、分类讨论?4、找准错题原因更重要?试卷关键字可做记号在高考备考中,每次考试和做题中一定要有始有终,每次在做题时能一步一步算准确,才能提高运算的准确度,避免计算失误!为了避免审题失误,在考试时一定要先把题仔细阅读一遍,可以把试卷上关键字做上记号来提示你充分而准确地利用已知条件。?
对高中数学教学的认识和探讨永远在路上 复习:统计与概率高中数学《题说》 ……
做之不能以其道,思之不能尽其法,错之而不能知其意,执笔而临之,曰:“此题难矣!”呜呼!其真难邪?其真不会做也。从总体中
逐个抽取将总体均分成几部分,按事先确定的规则在各部分抽取将总体分成几层,分层进行抽取在起始部分抽样时采用简单随机抽样各层抽样时采用简单随机抽样或系统抽样总体中的个体数较少总体中的个体数较多1、抽样方法总体由差异明显的几部分组成知识回顾 一般地,作频率分布直方图的步骤如下:(1)求极差。(2)决定组数和组距。
(3)分组。 (4)列出频率分布表;
(5)画出频率分布直方图(纵轴表示频率/组距).2、总体分布的估计知识回顾3、总体特征数的估计设一组样本数据 ,众数、中位数、
平均数、方差、标准差例:本次三模,数学有效试卷共116份,除去其他科未答满者3人,为便 于计算,再随机剔除3人,成绩分组以及各组的频 数如下:
[10,30),11; [30,50),31;
[50,70),27; [70,90),33; [90,110),8;
(1)列出样本的频率分布表
(2)画出频率分布直方图
(3)根据频率分布直方图求众数、中位数、平均数、方差
典型例题解:(1)样本的频率分布表如下:典型例题(2)频率分布直方图:典型例题(2)频率分布直方图:典型例题1:求某一组频率时,其中有两个组以上的纵坐标相等。
2:纵坐标为频率比组距,易与频 率混淆。
3:分层抽样时,人数易错。
频率分布直方图多出现在大题第一问, 是做概率的基础数据,一错全错!
总结易错处:独立性检验例:以三模与二模本班成绩做对比,问是否有90%的把握认为学习成绩上升与学习时间超过晚上12点有关?高考考查重点:
1、相互独立事件的概率.
2、n次独立重复试验的模型及二项分布.
辨析:
互斥事件、对立事件、相互独立事件相互独立与二项分布复习(1)独立重复试验
在相同条件下可重复进行的,各次之间相互独立的一种试验,在这种试验中每一次试验只有____结果,即要么发生,要么不发生,且任何一次试验中发生的概率都是______的.
(2)二项分布 进行n次试验,如果满足以下条件:
①每次试验只有两个相互独立的结果,
②“成功”的概率均为p,“失败”的概率均为1-p;
2.独立重复试验与二项分布两种一样③各次试验是相互独立的.
(1)设X为大黄在途中遇到红灯的次数,求X的分布列;
(2)设Y为大黄在首次停下来前经过的路口数,求Y的分布列;
(3)求大黄在途中至少遇到一次红灯的概率.
(2)由于Y表示这名学生在首次停车时经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5,6.
其中:{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.超几何分布与二项分布的区别和联系
① 超几何分布定义:一批产品共N件,其中有M件次品,随机取出的n件产品中,次品数x服从超几何分布,
超几何分布满足两个条件:一是抽取的产品不再放回,二是总产品数量N较小。
②二项分布定义:在n次独立重复试验中,每次试验A发生的概率均为p,那么在n次独立重复试验中,事件A恰好发生k次的概率,
则称X服从二项分布,记为X~B(n,p)
二项分布也满足两个条件:一是有放回、独立重复;二是恰好发生k次。
③当抽取的方式从无放回变为有放回或者总产品数量N很大时,超几何分布变为二项分布 .例:长时间用手机上网严重影响学生健康与学习,如果学生平均每周手机的时长超过30个小时,则被称为网瘾少年,为了解高三学生的手机上网情况,经统计,四班30人中有10人一周上网超过30小时,五班20人中有10人一周上网超过30小时。
(1)从四班的样本数据中抽取4人,求恰有1人是网瘾少年的概率
(2)从五班的样本中随机抽取4人,记网瘾少年人数为X,写出其分布列和数学期望(1)混淆“互斥”与“对立”、“互斥”与
“独立”而致误
(2)混淆“条件概率”与“相互独立事件的概
率”而致误
(3)混淆“二项分布”与“超几何分布”而致误
(4)忽视正态分布的图像而致误
(5)线性回归方程的性质不熟练而致误
(6)不理解独立性检验的思想而致误 统计与概率教学总结统计与概率教学总结 (1)注重培养学生阅读理解能力;
(2)注重提升学生数学建模能力;
(3)注重培养学生处理数据能力;
(4)注重提高学生准确运算能力。统计与概率教学总结 (1)对照考纲复习课本?吃透基本定义定理
(2)按照“知识-题型-方法-思想”构建知识
体系
(3)数学思想方法:函数、方程、数形结合、
分类讨论
(4)找错题原因更重要,试卷关键字作记号统计与概率教学总结正态分布下节任务单几何概型回归方程复习思路1、对照考纲复习课本?吃透基本定义定理2、按照“知识-题型-方法-思想”构建知识体系 3、数学思想方法:函数、方程、数形结合、分类讨论?4、找准错题原因更重要?试卷关键字可做记号在高考备考中,每次考试和做题中一定要有始有终,每次在做题时能一步一步算准确,才能提高运算的准确度,避免计算失误!为了避免审题失误,在考试时一定要先把题仔细阅读一遍,可以把试卷上关键字做上记号来提示你充分而准确地利用已知条件。?
