再探“杨辉三角”课件31张PPT
图片预览







文档简介
课件31张PPT。再探“杨辉三角”落实学科核心素养教学,培养学生自主学习能力。人教A版选修2-3第一章第三节《易·系辞上》
河出图 洛出书
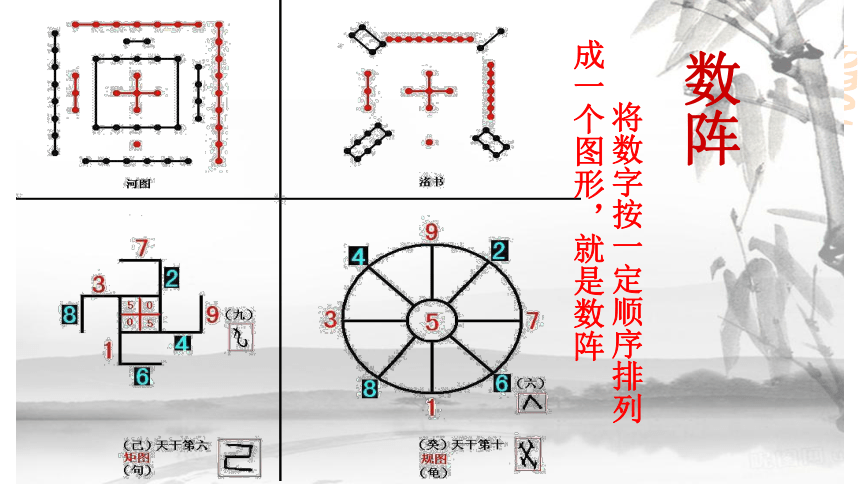
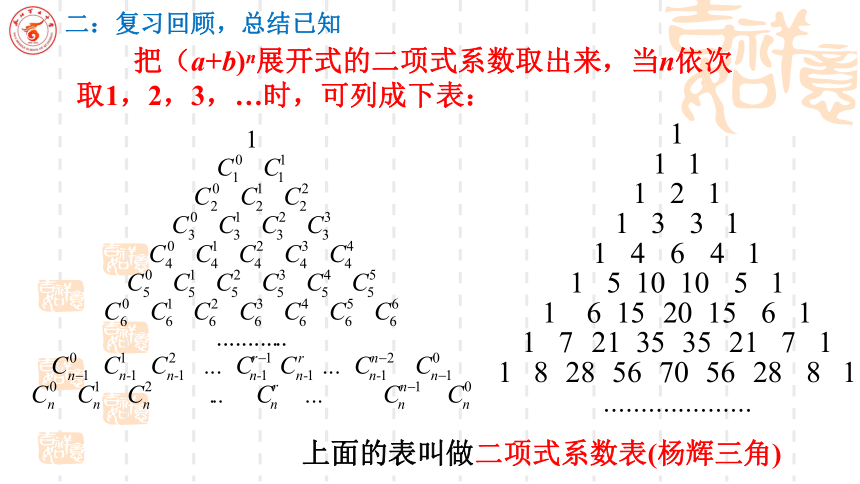
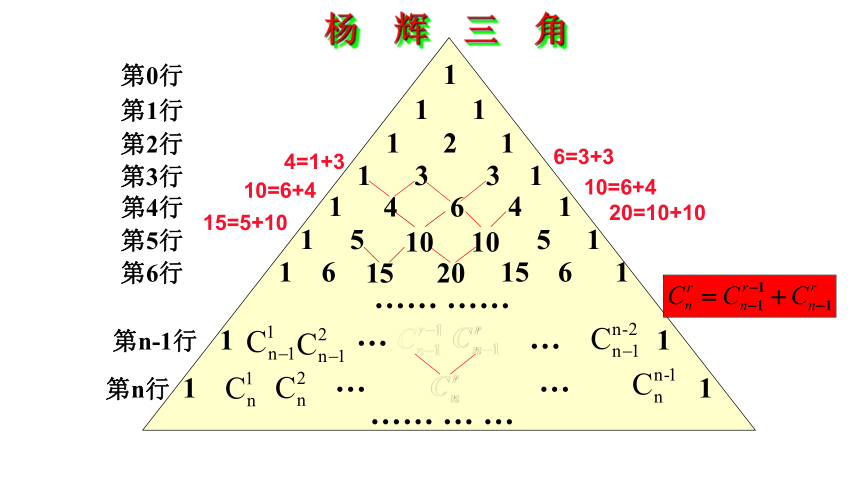
圣人则之一:引经据典,步入新课数阵 将数字按一定顺序排列成一个图形,就是数阵《九章算法》杨辉 开方作法本源图手算高次方根研究高阶等差级数(垛积术) 研究微积分差分方程、无穷级数 贾宪华罗庚朱世杰艾萨克·牛顿 把(a+b)n展开式的二项式系数取出来,当n依次取1,2,3,…时,可列成下表:上面的表叫做二项式系数表(杨辉三角)二:复习回顾,总结已知第5行 1 5 5 1第0行 1杨辉三角第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 1第6行 1 6 15 6 1第n-1行 1 1第n行 1 1…… …………………… … … 1515=5+102020=10+1010=6+41010=6+41066=3+34=1+34(1)对称性:
与首末两端“等距离”的两个二项式系数相等.(a+b)n展开式的二项式系数依次是: (3)增减性与最大值: (2)递推性:
除1以外的每一个数都等于它肩上两个数的和.从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.杨辉三角的基本性质(4)二项式系数的和:“横看成岭侧成峰,
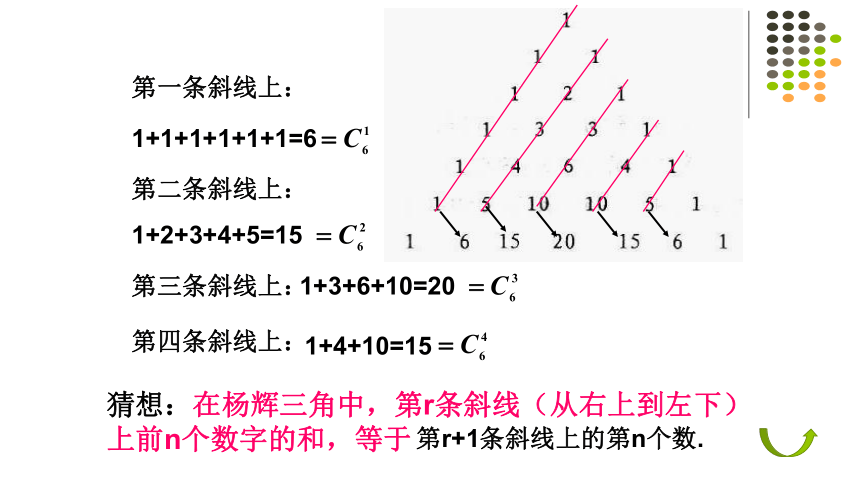
远近高低各不同。”三:小组合作,共探新知第一条斜线上:第二条斜线上:第三条斜线上:第四条斜线上:猜想:在杨辉三角中,第r条斜线(从右上到左下)上前n个数字的和,等于1+1+1+1+1+1=61+2+3+4+5=151+3+6+10=201+4+10=15第r+1条斜线上的第n个数.结论1:杨辉三角中,第m条斜(从右上到左下)上前n个数字的和,等于第m+1条斜线上第n个数即根据杨辉三角的对称性,类似可得:杨辉三角中,第m条斜(从左上到右下)上前n个数字的和,等于第m+1条斜线上第n个数。211 123581334 从第三个数起,任一数都等于前两个数的和;这就是著名的斐波那契数列 。此数列{an}满足, a1=1,a2=1,
且an=an-1+an-2 (n≥3)
这就是著名的斐波那契数列. 世事洞明皆数学,留心处处是文章。1,1,2,3,5,8,13,21,34,…此数列{an}满足, a1=1,a2=1, 且an=an-1+an-2 (n≥3)这就是著名的斐波那契数列. “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
杨辉三角与“纵横路线图”AB
杨辉三角与“纵横路线图” “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
杨辉三角与“纵横路线图”11231111113446551010151520353570 “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
由此看来,杨辉三角与纵横路线图问题有天然的联系 杨辉三角与“纵横路线图”112311111134465510101515203535701第5行 1 5 5 1第0行 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 1第6行 1 6 15 6 1第n行 11…… ……………… … … 1520101064第7行 1 7 21 35 35 21 7 1 五:教师补充,再得新知第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第n行 11…… ……………… … … 100000第7行 1 1 1 1 1 1 1 1 “0,1”三角形第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第n行 11…… ……………… … … 100000第7行 1 1 1 1 1 1 1 1 第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第7行 1 1 1 1 1 1 1 1 …… … … 1000001………… … … 第n行 1第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第7行 1 1 1 1 1 1 1 1 …… … … 1000001………… … … 第n行 1谢尔宾斯基三角形分形数学。谢尔宾斯基塔奇异、美丽的图案-----超出想象!这是数学
的杰作!华罗庚与杨辉三角的研究 华罗庚(1910-1985)是一位具有世界声誉的数学家,我国进入世界著名数学行列最杰出的代表。撰写10部专著、200篇论文和10余部科普著作。由于他的贡献,有许多定理、引理、不等式与方法等都用他的名字命名.在他的科普著作《从杨辉三角谈起》中,对杨辉三角的构成,提出了许多有趣的看法. 杨辉三角是数学之花,是中国古代数学得伟大成就。它有许多有趣的性质和用途。本节课所介绍的几个问题不过只是管中窥豹而已。同学们有兴趣的话可以找相关得专著来看。1、运用了联系、类比的观点看问题;
2、运用了从特殊到一般的归纳猜想与证明的思想方法;
3、“横看成岭侧成峰,远近高低各不同”——学习了从多角度看数阵;
4、锤炼发现问题、提出问题、解决问题的能力。六、探究小结,盘点新知
河出图 洛出书
圣人则之一:引经据典,步入新课数阵 将数字按一定顺序排列成一个图形,就是数阵《九章算法》杨辉 开方作法本源图手算高次方根研究高阶等差级数(垛积术) 研究微积分差分方程、无穷级数 贾宪华罗庚朱世杰艾萨克·牛顿 把(a+b)n展开式的二项式系数取出来,当n依次取1,2,3,…时,可列成下表:上面的表叫做二项式系数表(杨辉三角)二:复习回顾,总结已知第5行 1 5 5 1第0行 1杨辉三角第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 1第6行 1 6 15 6 1第n-1行 1 1第n行 1 1…… …………………… … … 1515=5+102020=10+1010=6+41010=6+41066=3+34=1+34(1)对称性:
与首末两端“等距离”的两个二项式系数相等.(a+b)n展开式的二项式系数依次是: (3)增减性与最大值: (2)递推性:
除1以外的每一个数都等于它肩上两个数的和.从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.杨辉三角的基本性质(4)二项式系数的和:“横看成岭侧成峰,
远近高低各不同。”三:小组合作,共探新知第一条斜线上:第二条斜线上:第三条斜线上:第四条斜线上:猜想:在杨辉三角中,第r条斜线(从右上到左下)上前n个数字的和,等于1+1+1+1+1+1=61+2+3+4+5=151+3+6+10=201+4+10=15第r+1条斜线上的第n个数.结论1:杨辉三角中,第m条斜(从右上到左下)上前n个数字的和,等于第m+1条斜线上第n个数即根据杨辉三角的对称性,类似可得:杨辉三角中,第m条斜(从左上到右下)上前n个数字的和,等于第m+1条斜线上第n个数。211 123581334 从第三个数起,任一数都等于前两个数的和;这就是著名的斐波那契数列 。此数列{an}满足, a1=1,a2=1,
且an=an-1+an-2 (n≥3)
这就是著名的斐波那契数列. 世事洞明皆数学,留心处处是文章。1,1,2,3,5,8,13,21,34,…此数列{an}满足, a1=1,a2=1, 且an=an-1+an-2 (n≥3)这就是著名的斐波那契数列. “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
杨辉三角与“纵横路线图”AB
杨辉三角与“纵横路线图” “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
杨辉三角与“纵横路线图”11231111113446551010151520353570 “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法? AB
由此看来,杨辉三角与纵横路线图问题有天然的联系 杨辉三角与“纵横路线图”112311111134465510101515203535701第5行 1 5 5 1第0行 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 1第6行 1 6 15 6 1第n行 11…… ……………… … … 1520101064第7行 1 7 21 35 35 21 7 1 五:教师补充,再得新知第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第n行 11…… ……………… … … 100000第7行 1 1 1 1 1 1 1 1 “0,1”三角形第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第n行 11…… ……………… … … 100000第7行 1 1 1 1 1 1 1 1 第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第7行 1 1 1 1 1 1 1 1 …… … … 1000001………… … … 第n行 1第5行 1 1 1 1第0行 1第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 1第6行 1 0 1 0 1第7行 1 1 1 1 1 1 1 1 …… … … 1000001………… … … 第n行 1谢尔宾斯基三角形分形数学。谢尔宾斯基塔奇异、美丽的图案-----超出想象!这是数学
的杰作!华罗庚与杨辉三角的研究 华罗庚(1910-1985)是一位具有世界声誉的数学家,我国进入世界著名数学行列最杰出的代表。撰写10部专著、200篇论文和10余部科普著作。由于他的贡献,有许多定理、引理、不等式与方法等都用他的名字命名.在他的科普著作《从杨辉三角谈起》中,对杨辉三角的构成,提出了许多有趣的看法. 杨辉三角是数学之花,是中国古代数学得伟大成就。它有许多有趣的性质和用途。本节课所介绍的几个问题不过只是管中窥豹而已。同学们有兴趣的话可以找相关得专著来看。1、运用了联系、类比的观点看问题;
2、运用了从特殊到一般的归纳猜想与证明的思想方法;
3、“横看成岭侧成峰,远近高低各不同”——学习了从多角度看数阵;
4、锤炼发现问题、提出问题、解决问题的能力。六、探究小结,盘点新知
