人教版七年级数学上册第一章 有理数--1.3.1 第1课时 有理数的加法法则 课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册第一章 有理数--1.3.1 第1课时 有理数的加法法则 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-14 15:01:55 | ||
图片预览





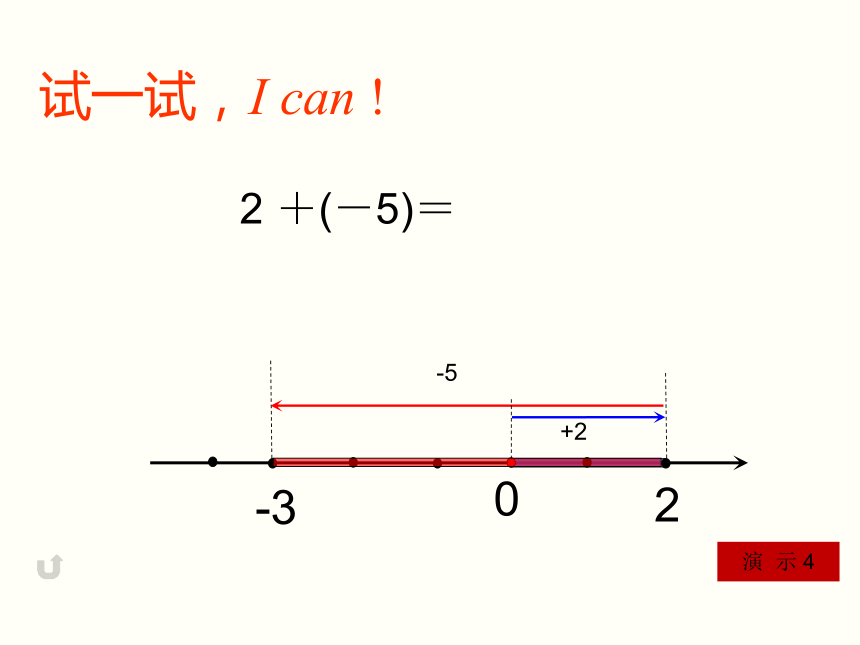
文档简介
(共30张PPT)
1.3 有理数的加减法
第一章 有理数
导入新课
讲授新课
当堂练习
课堂小结
学练优七年级数学上(RJ)
教学课件
第1课时 有理数的加法法则
1.3.1 有理数的加法
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
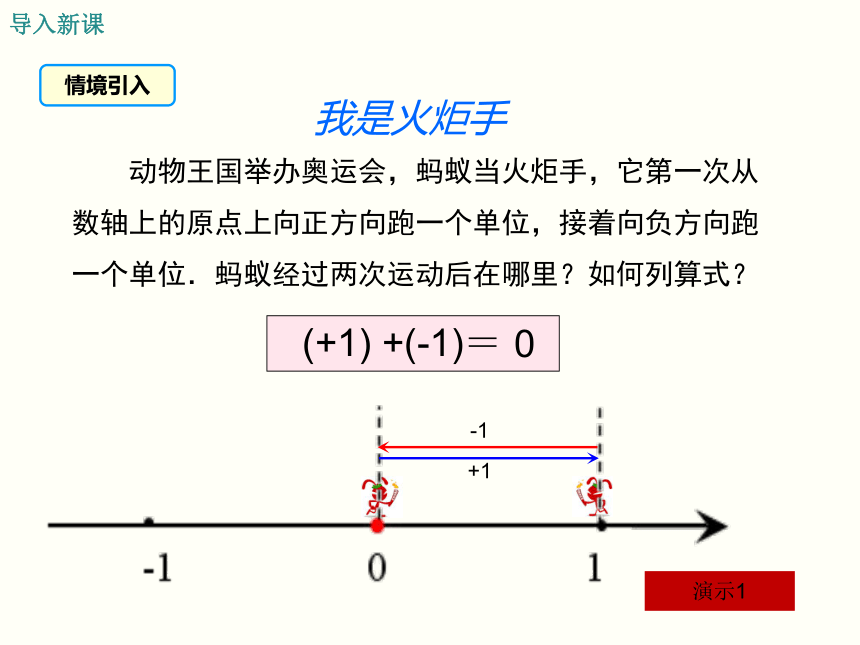
我是火炬手
演示1
+1
-1
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
导入新课
情境引入
8+(-8),(-3.5)+(+3.5)这两个算式的结果是多少呢?如何用上面的例子来解释?
讲授新课
合作探究
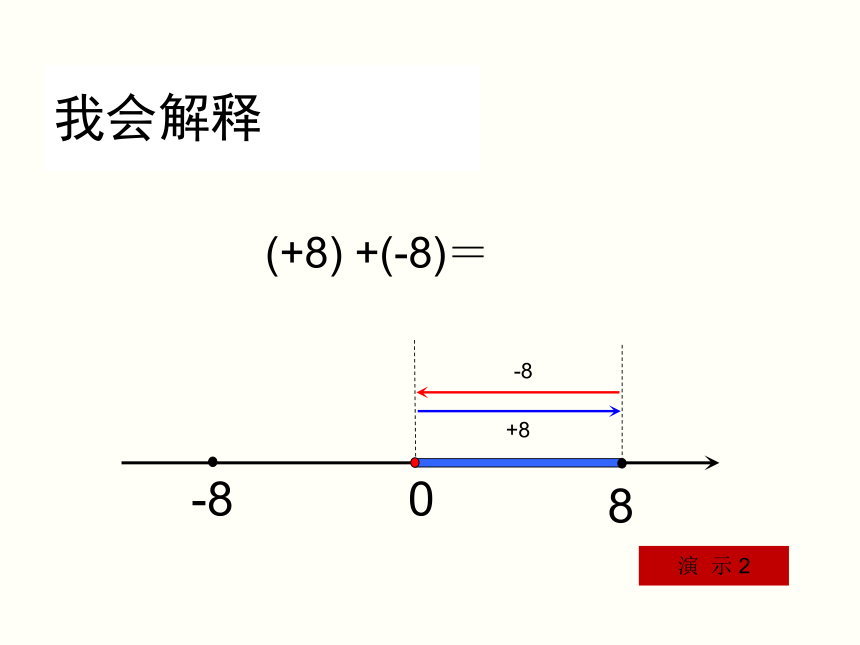
我会解释
(+8) +(-8)=
8
-8
0
+8
-8
演 示 2
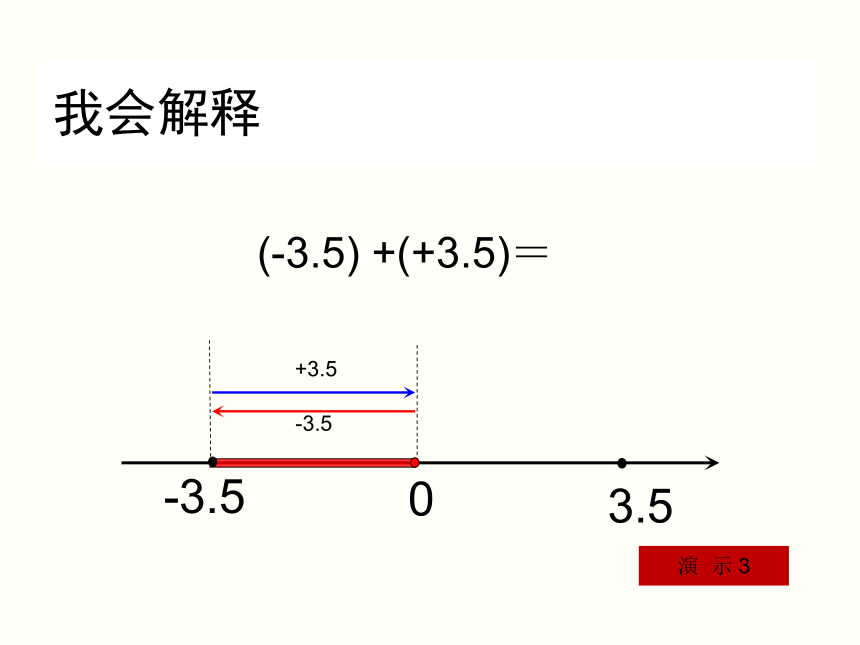
我会解释
(-3.5) +(+3.5)=
3.5
-3.5
0
-3.5
+3.5
演 示 3
(+1) +(-1)=0
8+(-8)=0
(-3.5)+(+3.5)=0
问题:观察上面算式中各个加数的特征及结果,你有什么发现?
仿照前面例子,尝试解释下面算式的结果.
(1) 2 +(-5)=
(2) 8 +(-6)=
(3) (-8) +5=
(4) 5 +3=
(5) (-2) +(-3)=
2
-3
0
-5
+2
演 示 4
试一试,I can !
2 +(-5)=
8
-2
0
-6
+8
演 示 5
试一试,I can !
8 +(-6)=
2
4
6
0
+5
-8
演 示 6
试一试,I can !
(-8) +(+5)=
-2
-4
-6
-8
-8
2
8
+5
演 示 7
试一试,I can !
+5 +(+3)=
6
4
2
0
+3
-2
0
-3
演 示 8
试一试,I can !
(-2) +(-3)=
-1
-2
-3
-4
-2
-5
1
你还能用其他方法来解释有理数的加法运算吗?小组讨论,并用你的方法解释以上五道算式的运算结果.
游戏规则
-1
+1
(+1) +(-1)=
演 示 9
-1与+1相加抵消,结果为0
-1
+1
表示+1
表示-1
0
利用游戏规则,如何解释下面算式的结果?
(1) 2 +(-5)=
(2) 8 +(-6)=
(3) (-8) +5=
(4) 5 +3=
(5) (-2) +(-3)=
演示
轻松解释(1)
-1
+1
-1
-1
-1
-1
+1
(+2) +(-5)=
演示
轻松解释(2)
(+8) +(-6)=
演示
轻松解释(3)
(-8) +(+5)=
+1
-1
-1
演示
轻松解释(4)
5 +(+3)=
+1
+1
+1
+1
+1
+1
+1
+1
演示
轻松解释(5)
(-2) +(-3)=
-1
-1
-1
-1
-1
两个有理数相加,和的符号怎样确定?
和的绝对值如何确定?
讨论:
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
总结归纳
例1 计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.
典例精析
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0
互为相反意义的量可以全部抵消或部分抵消.
例2 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
红队 黄队 蓝队 净胜球
红队 4:1 0:1 2
黄队 1:4 1:0 -2
蓝队 1:0 0:1 0
解:每个队的进球总数记为正数,失球总数记为负数,
这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数
为( ).
1
1
(+1)+(-1)=0
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3);?? (6)(-1.9)+(-0.11);
(7)(-9.18)+6.18; (8)4.2+(-6.7).
当堂练习
计算
答案:(1)-3.3 (2)-4.7 (3)2.4 (4)5
(5)3.7 (6)-2.01 (7)-3 (8)-2.5
学科网
课堂小结
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
见《学练优》本课时练习
课后作业
1.3 有理数的加减法
第一章 有理数
导入新课
讲授新课
当堂练习
课堂小结
学练优七年级数学上(RJ)
教学课件
第1课时 有理数的加法法则
1.3.1 有理数的加法
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
我是火炬手
演示1
+1
-1
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
导入新课
情境引入
8+(-8),(-3.5)+(+3.5)这两个算式的结果是多少呢?如何用上面的例子来解释?
讲授新课
合作探究
我会解释
(+8) +(-8)=
8
-8
0
+8
-8
演 示 2
我会解释
(-3.5) +(+3.5)=
3.5
-3.5
0
-3.5
+3.5
演 示 3
(+1) +(-1)=0
8+(-8)=0
(-3.5)+(+3.5)=0
问题:观察上面算式中各个加数的特征及结果,你有什么发现?
仿照前面例子,尝试解释下面算式的结果.
(1) 2 +(-5)=
(2) 8 +(-6)=
(3) (-8) +5=
(4) 5 +3=
(5) (-2) +(-3)=
2
-3
0
-5
+2
演 示 4
试一试,I can !
2 +(-5)=
8
-2
0
-6
+8
演 示 5
试一试,I can !
8 +(-6)=
2
4
6
0
+5
-8
演 示 6
试一试,I can !
(-8) +(+5)=
-2
-4
-6
-8
-8
2
8
+5
演 示 7
试一试,I can !
+5 +(+3)=
6
4
2
0
+3
-2
0
-3
演 示 8
试一试,I can !
(-2) +(-3)=
-1
-2
-3
-4
-2
-5
1
你还能用其他方法来解释有理数的加法运算吗?小组讨论,并用你的方法解释以上五道算式的运算结果.
游戏规则
-1
+1
(+1) +(-1)=
演 示 9
-1与+1相加抵消,结果为0
-1
+1
表示+1
表示-1
0
利用游戏规则,如何解释下面算式的结果?
(1) 2 +(-5)=
(2) 8 +(-6)=
(3) (-8) +5=
(4) 5 +3=
(5) (-2) +(-3)=
演示
轻松解释(1)
-1
+1
-1
-1
-1
-1
+1
(+2) +(-5)=
演示
轻松解释(2)
(+8) +(-6)=
演示
轻松解释(3)
(-8) +(+5)=
+1
-1
-1
演示
轻松解释(4)
5 +(+3)=
+1
+1
+1
+1
+1
+1
+1
+1
演示
轻松解释(5)
(-2) +(-3)=
-1
-1
-1
-1
-1
两个有理数相加,和的符号怎样确定?
和的绝对值如何确定?
讨论:
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
总结归纳
例1 计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.
典例精析
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0
互为相反意义的量可以全部抵消或部分抵消.
例2 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
红队 黄队 蓝队 净胜球
红队 4:1 0:1 2
黄队 1:4 1:0 -2
蓝队 1:0 0:1 0
解:每个队的进球总数记为正数,失球总数记为负数,
这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数
为( ).
1
1
(+1)+(-1)=0
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3);?? (6)(-1.9)+(-0.11);
(7)(-9.18)+6.18; (8)4.2+(-6.7).
当堂练习
计算
答案:(1)-3.3 (2)-4.7 (3)2.4 (4)5
(5)3.7 (6)-2.01 (7)-3 (8)-2.5
学科网
课堂小结
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
见《学练优》本课时练习
课后作业
