北师大版七上数学第四章基本平面图形章末课堂练习(含答案)
文档属性
| 名称 | 北师大版七上数学第四章基本平面图形章末课堂练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 08:47:01 | ||
图片预览

文档简介
北师大版七上数学第四章基本平面图形复习课同步课堂练习
判断题
射线没有端点.
平角是一条直线.
延长线段AB到C,使BC=AB.
射线AB与射线BA表示同一条射线.
过一点有且只有一条直线与已知直线平行.
垂直于同一直线的两直线互相垂直.
7.平行于同一直线的两直线互相平行.
8.大于90°的角是钝角.
选择题
1.两个锐角的和( )
A.一定是锐角 B.一定是直角
C.一定是钝角 D.可能是钝角、直角或钝角
2.平角上有三点A、B、C,如果AB=8,AC=5,BC=3,则( )
点C在线段AB上
点C在线段AB的延长线上
点C在直线AB外
点C可能在直线AB上,也可能在直线AB外
3.如图,B、C是线段AD上任意两点,M是AB的中点,N是CD的中点,若MN=a,BC=b.则线段AD的长是( )
A、2(a-b) B、2a-b
C、a+b D、a-b
4.已知∠AOB=30°,∠BOC=80°,∠AOC=50°,那么( )
射线OB在∠AOC内
射线OB在∠AOC外
射线OB与射线OA重合
射线OB与射线OC重合
5.如图所示,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )
A、75° B、15° C、105° D、165°
6.在海上,灯塔位于一艘船的北偏东40°方向,那么这艘船位于这个灯塔的( )
A、南偏西50°方向 B、南偏西40°方向
C、北偏东50°方向 D、北偏东40°方向
填空题
不在同一直线上的四点最多能确定________条直线。
如图,点C、D、E在线段AB上,且AC=CD=DE=EB,则图中相等的线段还有______。
如图所示,点C是∠AOB的边OA上一点,D、E是OB上两点,则图中共有_________长线段;________射线;_______个小于平角的角。
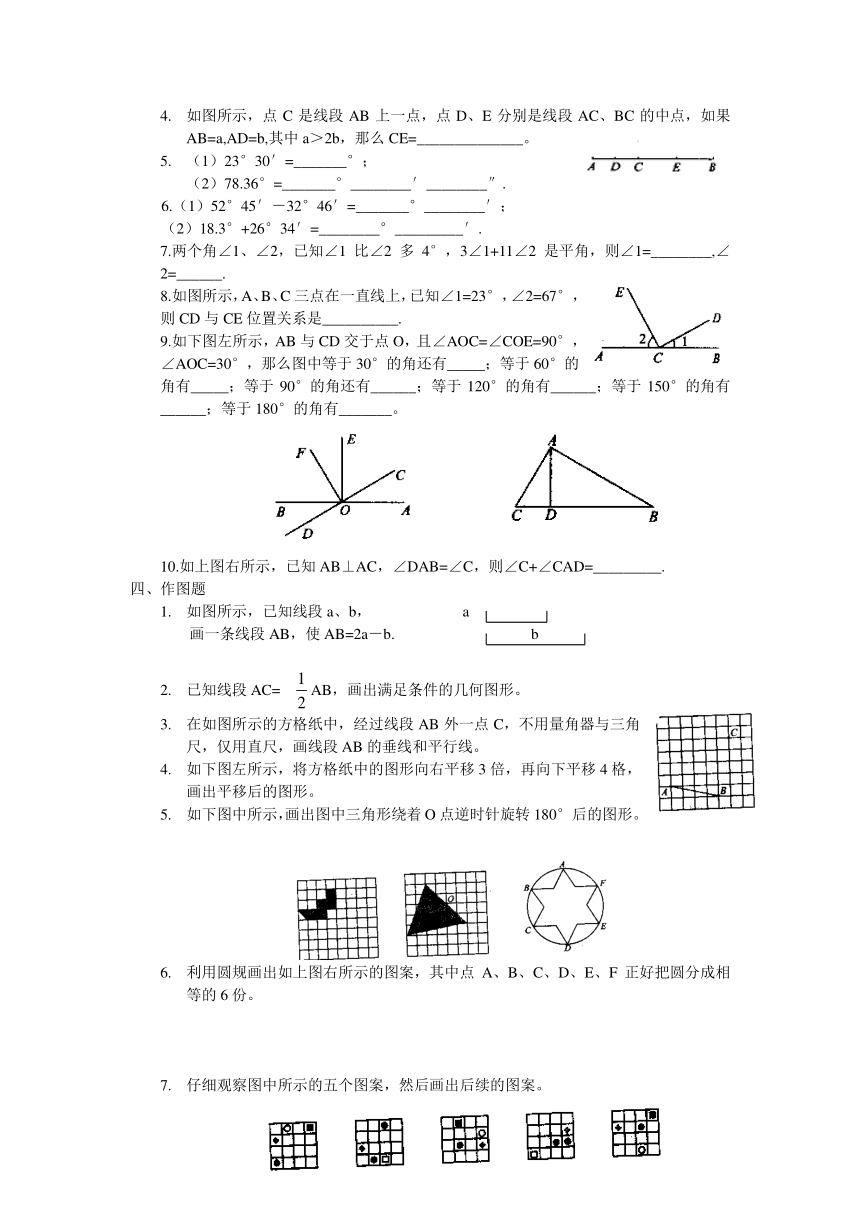
如图所示,点C是线段AB上一点,点D、E分别是线段AC、BC的中点,如果AB=a,AD=b,其中a>2b,那么CE=______________。
(1)23°30′=_______°;
(2)78.36°=_______°________′________″.
6.(1)52°45′-32°46′=_______°________′;
(2)18.3°+26°34′=________°_________′.
7.两个角∠1、∠2,已知∠1比∠2多4°,3∠1+11∠2是平角,则∠1=________,∠2=______.
8.如图所示,A、B、C三点在一直线上,已知∠1=23°,∠2=67°,则CD与CE位置关系是__________.
9.如下图左所示,AB与CD交于点O,且∠AOC=∠COE=90°,∠AOC=30°,那么图中等于30°的角还有_____;等于60°的角有_____;等于90°的角还有______;等于120°的角有______;等于150°的角有______;等于180°的角有_______。
10.如上图右所示,已知AB⊥AC,∠DAB=∠C,则∠C+∠CAD=_________.
作图题
如图所示,已知线段a、b, a
画一条线段AB,使AB=2a-b. b
已知线段AC=AB,画出满足条件的几何图形。
在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线和平行线。
如下图左所示,将方格纸中的图形向右平移3倍,再向下平移4格,画出平移后的图形。
如下图中所示,画出图中三角形绕着O点逆时针旋转180°后的图形。
利用圆规画出如上图右所示的图案,其中点A、B、C、D、E、F正好把圆分成相等的6份。
仔细观察图中所示的五个图案,然后画出后续的图案。
计算题
1. 51°37′-32°45′31″ 2. 35°35′35″×5
3. (180°-91°32′24″)2 4. 176°51′3
5. 把34.37°化成度、分、秒 6. 把26°17′42″化成度
解答题
用两条直线最多可以把一个平面分成几部分?3条直线呢?4条直线呢?平面上有(a)4条、(b)5条、(c)6条直线,其中任意两条不平行,任意三条不交于同一点,它们把平面分成几部分?你能总结出什么规律吗?
在纸上画出四个点(其中任意三点不在同一条直线上),经过每两个点用直尺画一条直线,一共可以画几条?画出所有直线,并指出图中以这四个点为端点的线段及射线的条数。
如图所示是一副三角尺拼成的两个图案。
确定图(1)中所示是一副三角尺拼成的两个图案。
在图(2)中,求∠EFC、∠CED、∠AFC的度数。
适当地剪几刀,就可以把上图中的十字变成一个正方形,有人说剪两刀就可以了,你相信吗?不妨试试看。
能否将4支铅笔排成如图所示的形状?你能否设计一个事实上不存在的图形?
参考答案
一、1.× 2.× 3.√ 4.×
5.× 6.× 7.√ 8.×
二、1.D 2.A 3.B 4.B
5.C 6.B
三、1. 6 2.AD=CE=DB、AE=CB 3.6;5 ;10
4. 5.(1)23.5° (2)78°21′36″
6.(1)19°59′ (2)44°52′ 7. 16°; 12° 8. 垂直
9.∠FOE、∠BOD; ∠COE、∠BOF; ∠BOE、∠DOF; ∠AOF、∠DOE;
∠BOC; ∠AOB、∠COD
10.90
四、
1.如图所示,AB=2a-b
2.图略。有三种情况:①点C在线段AB上;②点C在线段BA延长线上;③点C在直线AB外
3.如图所示,CB⊥AB,CD∥AB
4.如图所示即为平移后的图形
5.如图所示,右上为旋转后的图形,右下为原图形
6.略
7.如图所示
五、1. 18°51′29″ 2. 177°57′55″ 3. 44°13′48″
5.34°22′12″ 6.26.295°
六、1. .两条直线可以把平面分成4部分.3条直线(直线相互不平行也不通过同一个点)把平面分成7部分,如图所示、作第4条直线,它与前3条直线交于3点,这3点把第4条直线分成4段,相应地平面也就增加了4部分,所示4条直线把平面分成7+4=11部分,作第5条直线,它被分成5段,相应地平面增加5部分,所以5条直线把平面分成7+4+5=16部分,于是6条直线把平面分成7+4+5+6=22部分。事实上,1条直线把平面分成2部分,2条直线把平面分成2+2=4部分,3条直线把平面分成2+2+3=7部分,……,那么条直线把平面分成2+2+3+4+…+=部分。
2.提示:∵∠BOC-∠AOC=(∠BOD+∠COD)-(∠AOD-∠COD)=∠BOD+∠COD-∠AOD+∠COD=2∠COD=30°,∴∠COD=15°
3.如图所示,经过纸上四点(其中每三个点不在同一直线上)有6条直线,图中以这四个点为端点的线段有6条,射线有24条
4.(1)∠A=60°,∠ABC=90°,∠ABD=135°,∠ACB=30°,∠ACD=75°,∠D=90°∠BCD=45°,∠CBD=45°;(2)∠EFC=45°,∠CED=60°,∠AFC=135°。
5.如图所示,左图为原图,上画的虚线是剪切线,右图为剪拼后的图形
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
