12.3 角的平分线的性质(要点讲解+当堂检测+答案) 第1课时 学案
文档属性
| 名称 | 12.3 角的平分线的性质(要点讲解+当堂检测+答案) 第1课时 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:26:50 | ||
图片预览

文档简介
人教版数学八年级上册同步学案
第十二章 全等三角形
12.3 角的平分线的性质
第1课时 角的平分线的性质
要 点 讲 解
要点一 角平分线的作法
1. 一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线叫做角的平分线.作已知角的平分线的方法有很多,主要有折叠法和尺规作图法,尺规作图法是常用的方法,尺规作图一定要保留作图痕迹,并且要有结论.
2. 角平分线的画法是以“三边分别相等的两个三角形全等”和“全等三角形的对应角相等”的性质为理论根据的.作已知角的平分线的方法有多种,除了常用的尺规作图法外,还可以用三角板、角尺等作图.
经典例题1 分别画出已知钝角和平角的平分线.
解:钝角∠AOB的平分线的作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(2)分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部交于点C;
(3)画射线OC.射线OC即为所求,如图①所示.
图① 图②
用同样的作法作平角的平分线如图②所示.
要点二 角的平分线的性质
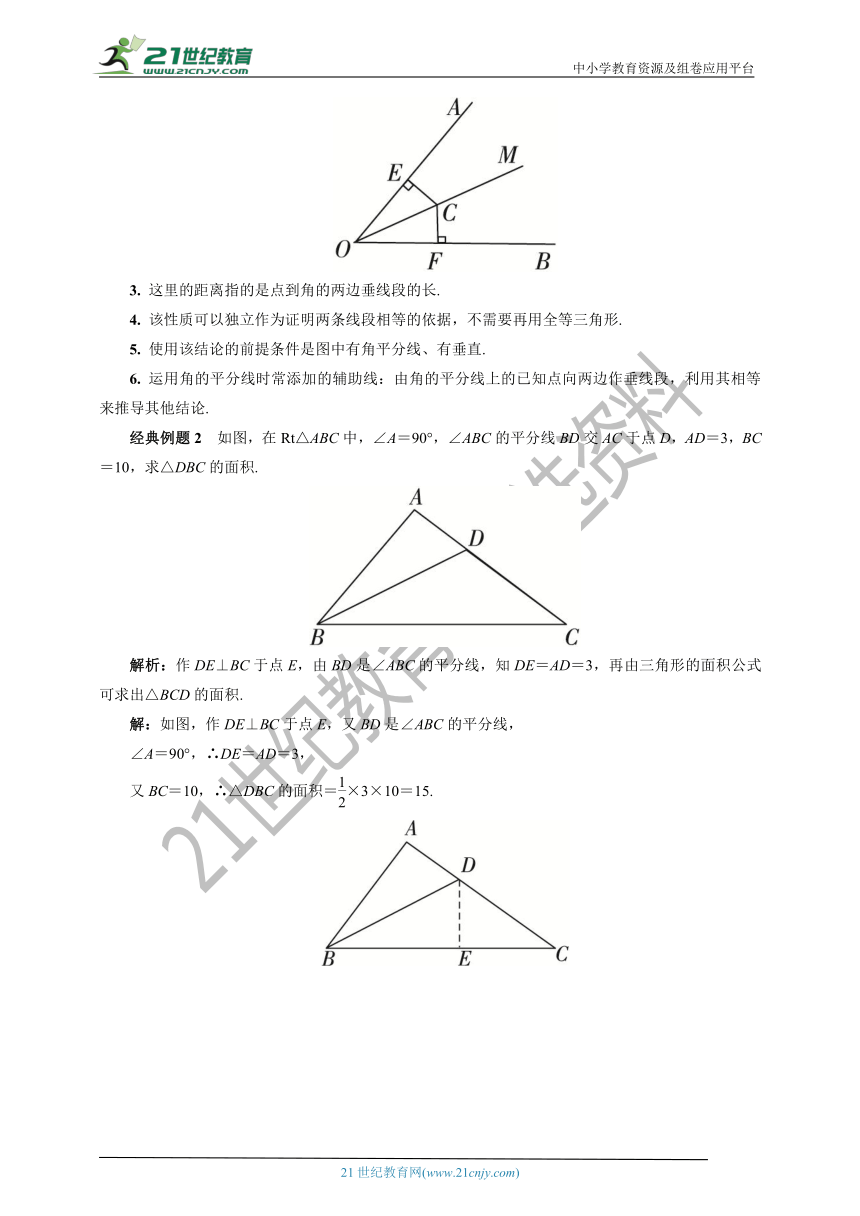
1. 角的平分线上的点到角的两边的距离相等.
2. 书写格式:如图所示,∵OM是∠AOB的平分线,C是OM上一点,CE⊥OA于点E,CF⊥OB于点F,∴CE=CF.
3. 这里的距离指的是点到角的两边垂线段的长.
4. 该性质可以独立作为证明两条线段相等的依据,不需要再用全等三角形.
5. 使用该结论的前提条件是图中有角平分线、有垂直.
6. 运用角的平分线时常添加的辅助线:由角的平分线上的已知点向两边作垂线段,利用其相等来推导其他结论.
经典例题2 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,求△DBC的面积.
解析:作DE⊥BC于点E,由BD是∠ABC的平分线,知DE=AD=3,再由三角形的面积公式可求出△BCD的面积.
解:如图,作DE⊥BC于点E,又BD是∠ABC的平分线,
∠A=90°,∴DE=AD=3,
又BC=10,∴△DBC的面积=×3×10=15.
当 堂 检 测
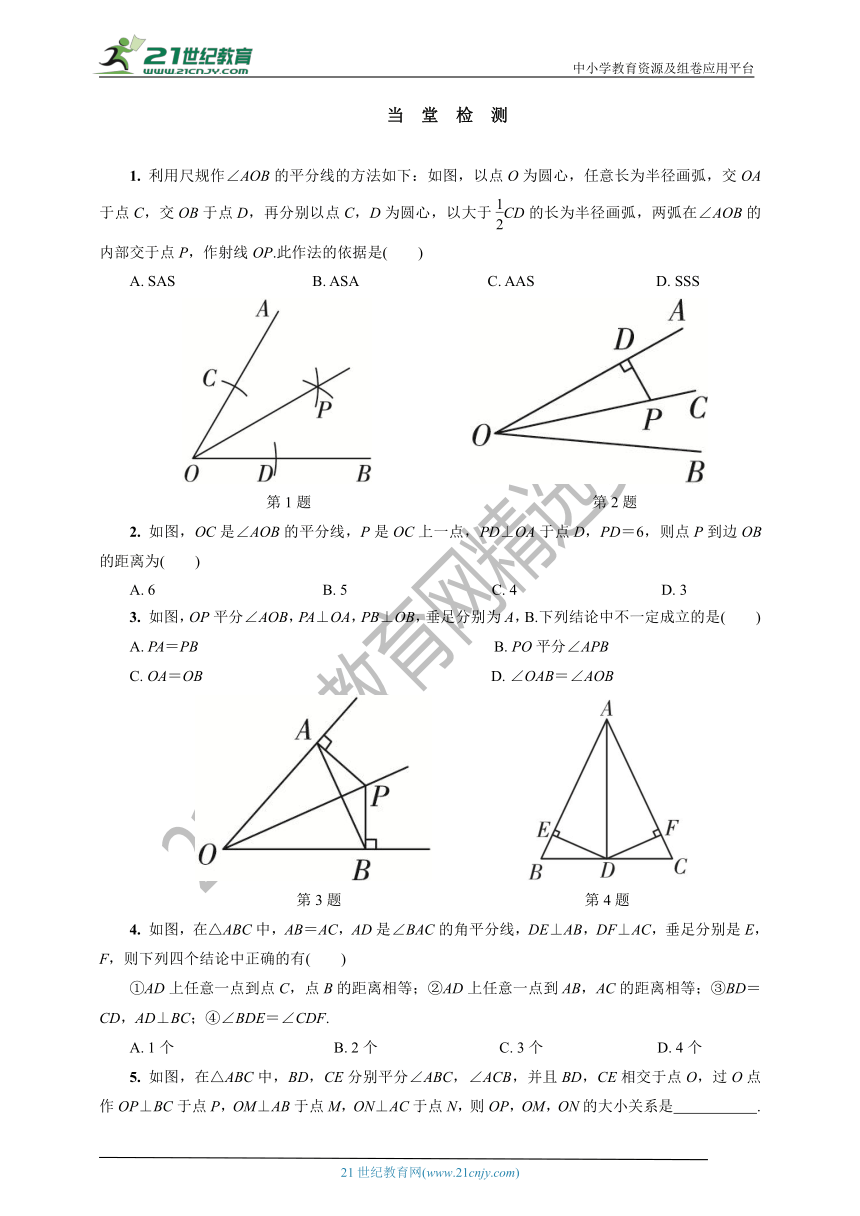
1. 利用尺规作∠AOB的平分线的方法如下:如图,以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D,再分别以点C,D为圆心,以大于CD的长为半径画弧,两弧在∠AOB的内部交于点P,作射线OP.此作法的依据是( )
A. SAS B. ASA C. AAS D. SSS
第1题 第2题
2. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A. 6 B. 5 C. 4 D. 3
3. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A. PA=PB B. PO平分∠APB
C. OA=OB D. ∠OAB=∠AOB
第3题 第4题
4. 如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论中正确的有( )
①AD上任意一点到点C,点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.
A. 1个 B. 2个 C. 3个 D. 4个
5. 如图,在△ABC中,BD,CE分别平分∠ABC,∠ACB,并且BD,CE相交于点O,过O点作OP⊥BC于点P,OM⊥AB于点M,ON⊥AC于点N,则OP,OM,ON的大小关系是 .
第5题 第6题
6. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
7. 如图,△ABC的角平分线AD交BC于点D,BD∶DC=2∶1.若AC=3cm,则AB= .
8. 已知△ABC,在△ABC内求作一点P,使它到△ABC三边的距离相等.
9. 如图,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.
求证:PM=PN.
当堂检测参考答案
1. D 2. A 3. D 4. D
5. OP=OM=ON
6. 4
7. 6cm
8. 解:如图,分别作∠A,∠B的平分线交于点P,则点P到△ABC三边的距离相等.
9. 证明:∵BD为∠ABC的平分线,∴∠ABD=∠CBD.在△ABD和△CBD中, ∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB.∵点P在BD上,PM⊥AD,PN⊥CD,∴PM=PN.
第十二章 全等三角形
12.3 角的平分线的性质
第1课时 角的平分线的性质
要 点 讲 解
要点一 角平分线的作法
1. 一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线叫做角的平分线.作已知角的平分线的方法有很多,主要有折叠法和尺规作图法,尺规作图法是常用的方法,尺规作图一定要保留作图痕迹,并且要有结论.
2. 角平分线的画法是以“三边分别相等的两个三角形全等”和“全等三角形的对应角相等”的性质为理论根据的.作已知角的平分线的方法有多种,除了常用的尺规作图法外,还可以用三角板、角尺等作图.
经典例题1 分别画出已知钝角和平角的平分线.
解:钝角∠AOB的平分线的作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(2)分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部交于点C;
(3)画射线OC.射线OC即为所求,如图①所示.
图① 图②
用同样的作法作平角的平分线如图②所示.
要点二 角的平分线的性质
1. 角的平分线上的点到角的两边的距离相等.
2. 书写格式:如图所示,∵OM是∠AOB的平分线,C是OM上一点,CE⊥OA于点E,CF⊥OB于点F,∴CE=CF.
3. 这里的距离指的是点到角的两边垂线段的长.
4. 该性质可以独立作为证明两条线段相等的依据,不需要再用全等三角形.
5. 使用该结论的前提条件是图中有角平分线、有垂直.
6. 运用角的平分线时常添加的辅助线:由角的平分线上的已知点向两边作垂线段,利用其相等来推导其他结论.
经典例题2 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,求△DBC的面积.
解析:作DE⊥BC于点E,由BD是∠ABC的平分线,知DE=AD=3,再由三角形的面积公式可求出△BCD的面积.
解:如图,作DE⊥BC于点E,又BD是∠ABC的平分线,
∠A=90°,∴DE=AD=3,
又BC=10,∴△DBC的面积=×3×10=15.
当 堂 检 测
1. 利用尺规作∠AOB的平分线的方法如下:如图,以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D,再分别以点C,D为圆心,以大于CD的长为半径画弧,两弧在∠AOB的内部交于点P,作射线OP.此作法的依据是( )
A. SAS B. ASA C. AAS D. SSS
第1题 第2题
2. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A. 6 B. 5 C. 4 D. 3
3. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A. PA=PB B. PO平分∠APB
C. OA=OB D. ∠OAB=∠AOB
第3题 第4题
4. 如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论中正确的有( )
①AD上任意一点到点C,点B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.
A. 1个 B. 2个 C. 3个 D. 4个
5. 如图,在△ABC中,BD,CE分别平分∠ABC,∠ACB,并且BD,CE相交于点O,过O点作OP⊥BC于点P,OM⊥AB于点M,ON⊥AC于点N,则OP,OM,ON的大小关系是 .
第5题 第6题
6. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
7. 如图,△ABC的角平分线AD交BC于点D,BD∶DC=2∶1.若AC=3cm,则AB= .
8. 已知△ABC,在△ABC内求作一点P,使它到△ABC三边的距离相等.
9. 如图,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.
求证:PM=PN.
当堂检测参考答案
1. D 2. A 3. D 4. D
5. OP=OM=ON
6. 4
7. 6cm
8. 解:如图,分别作∠A,∠B的平分线交于点P,则点P到△ABC三边的距离相等.
9. 证明:∵BD为∠ABC的平分线,∴∠ABD=∠CBD.在△ABD和△CBD中, ∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB.∵点P在BD上,PM⊥AD,PN⊥CD,∴PM=PN.
