1.1.2 导数的概念(课件27张PPT)
文档属性
| 名称 | 1.1.2 导数的概念(课件27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:21:47 | ||
图片预览







文档简介
课件27张PPT。第一章 导数及其应用
1.1 变化率与导数人教A版普通高中课程标准实验教科书
数学选修2-2第一章1.1十七世纪的三大数学发明 恩格斯在他的著作《自然辩证法》中,把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明. 数学来源于生活,应用于生活。十六世纪与 十七世纪,随着欧洲社会生产力的蓬勃发展,出现了许多重大的科学问题,对科学技术提出了全新的要求,比如:机械的普遍使用引起了对机械运动规律的研究,武器的进步刺激了弹道学的研究。解决这些问题需要新的数学工具,这促进了数学的发展,造就了众多伟大的数学家,他们的数学研究成果应用在很多领域,包括科学、工程、机械、军事、医学与经济学等。 走进数学史 了解“微积分” 变化是自然界的普遍现象,丰富多彩的变化问题随处可见.函数是描述运动变化规律的重要工具. 如何定量刻画千变万化的变化现象,是数学研究的重要课题. 17世纪创立的微积分就源于研究运动物体的变化规律,它是数学发展中的里程碑 . 历史上,牛顿与莱布尼茨分别独立创立了微积分. 公元1684年,莱布尼茨发表关于微积分的论文. 而牛顿在1671年发表了代表微积分发明的论文《流数术》. 微积分的创立与处理四类科学问题直接相关. 一是已知物体运动的路程关于时间的函数,求物体在任意时刻的速度与加速度,反之,已知物体的加速度关于时间的函数,求速度与路程;二是求曲线的切线;三是求函数的最大值与最小值;四是求长度、面积、体积和重心等.牛顿(Isaac Newton,1642—1727,英国),被誉为人类历史上最伟大的科学家之一,他创立了微积分,并且构筑了力学的大厦。
物理的尽头是数学,
数学的尽头是哲学. 莱布尼茨(Gottfried Wilhelm Leibniz,1646-1716,德国),是德国最重要的数学家和哲学家,一个举世罕见的科学天才,和牛顿同为微积分的创建人。他所创设的微积分符号远远优于牛顿的符号,这对微积分的发展有极大的影响。
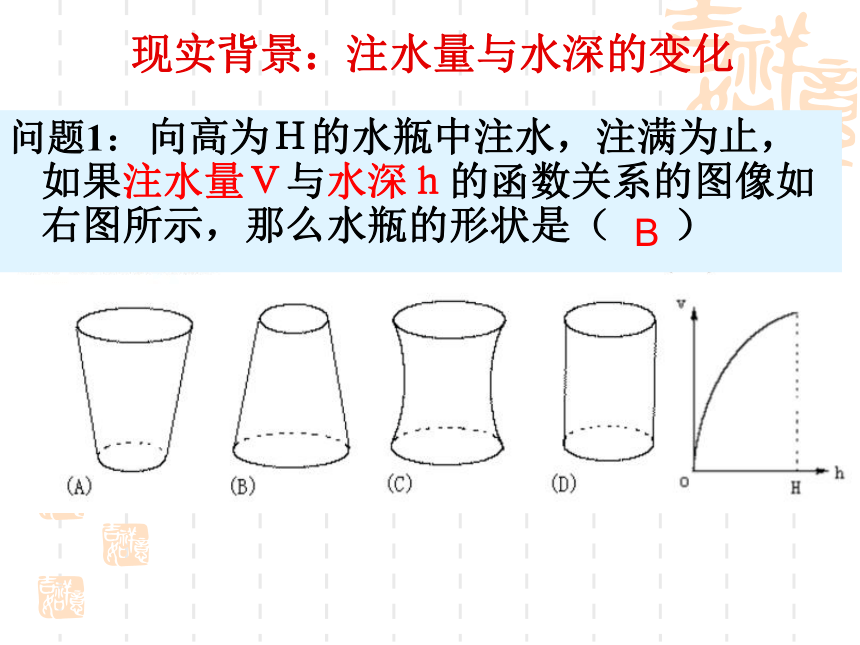
现实背景:注水量与水深的变化问题1:向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图像如右图所示,那么水瓶的形状是( ) B问题2:你吹过气球吗?回忆吹气球的过程
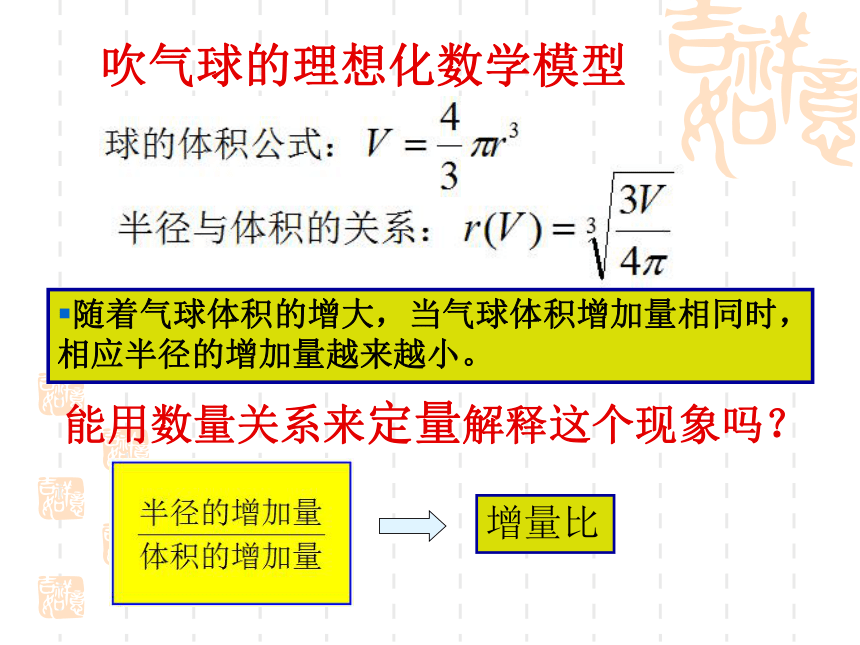
有什么变化现象?这些变化的快慢怎样?随着气球内空气容量的增加,气球的半径增加得越来越慢。你能从数学的角度,描述和解析这种变化快慢的现象吗?吹气球的理想化数学模型随着气球体积的增大,当气球体积增加量相同时,相应半径的增加量越来越小。 能用数量关系来定量解释这个现象吗?增量比你能用数量关系来定量解释这个现象吗?看图说话随着气球体积的增大,当气球体积增加量相同时,相应半径的增加量越来越小。 现实背景:高台跳水问题问题3:(1)请你计算,在 这段时间内运动员的平均速度;(2)请你计算,在 这段时间内运动员的平均速度.问题4:从个别到一般-----
用数学的眼光看问题自变量的改变量函数值的改变量平均变化率是描述变化快慢的 重要指标问题5:物体的平均速度能否精确反映它的运动状态??现实背景:高台跳水问题问题6:问题6—1:2s左右怎样表示?问题6—2:在2s “瞬间”的平均速度是什么? 化简变形“极限”是什么?无穷小量…无穷大…无限接近…逼近…庄子:一尺之棰,日取其半,万世不竭.刘徽的“割圆术”:割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣.基本思想:无限分割,以直代曲.重要意义极限(limit)运动员在某一时刻t0的瞬时速度怎样表示? 瞬时变化率问题7:依照前面的研究,你能给出函数y=f(x)在x=x0处的瞬时变化率的定义吗?这是与x0有关的确定值 ---- 导数体验导数的力量生活中的微积分 由导数的定义,我们知道:
高度 h 关于时间 t 的导数就是运动员
的 ;气球半径 r 关于体积 v 的导数就是气球的 .
牛顿:速度v关于时间t的导数是 .
瞬时速度瞬时膨胀率 实际上,导数可以描述任何事物的变化率,如效率、国内生产总值GDP的增长率,等等.瞬时加速度导数是微积分的核心概念之一微积分是数学中的一门中心学科,是从数学的角度研究变化,在涉及变化的地方,我们总会发现微积分。
历史上有两个伟大的人物牛顿和莱布尼茨对微积分的发展作出了杰出的贡献。
牛顿研究微积分着重于从运动学来考虑,莱布尼茨却是侧重于几何学来考虑。
牛顿建立了无穷小概念,从而奠定了微积分的基础。
课后作业阅读教材第6页例1
完成教材第10页习题1.1第3题
阅读教材第61页“走进微积分”
有兴趣的同学课后可上网查阅有关微积分创建的故事,了解微积分创建的意义和伟大功绩。
数学就是这样一种东西:她提醒你有无形的灵魂,她赋予她所发现的真理以生命;她唤起心神,澄清智慧;她给我们的内心思想增添光辉;她涤尽我们有生以来的蒙昧与无知。——Proclus谢谢!
再见!
数学选修2-2第一章1.1十七世纪的三大数学发明 恩格斯在他的著作《自然辩证法》中,把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明. 数学来源于生活,应用于生活。十六世纪与 十七世纪,随着欧洲社会生产力的蓬勃发展,出现了许多重大的科学问题,对科学技术提出了全新的要求,比如:机械的普遍使用引起了对机械运动规律的研究,武器的进步刺激了弹道学的研究。解决这些问题需要新的数学工具,这促进了数学的发展,造就了众多伟大的数学家,他们的数学研究成果应用在很多领域,包括科学、工程、机械、军事、医学与经济学等。 走进数学史 了解“微积分” 变化是自然界的普遍现象,丰富多彩的变化问题随处可见.函数是描述运动变化规律的重要工具. 如何定量刻画千变万化的变化现象,是数学研究的重要课题. 17世纪创立的微积分就源于研究运动物体的变化规律,它是数学发展中的里程碑 . 历史上,牛顿与莱布尼茨分别独立创立了微积分. 公元1684年,莱布尼茨发表关于微积分的论文. 而牛顿在1671年发表了代表微积分发明的论文《流数术》. 微积分的创立与处理四类科学问题直接相关. 一是已知物体运动的路程关于时间的函数,求物体在任意时刻的速度与加速度,反之,已知物体的加速度关于时间的函数,求速度与路程;二是求曲线的切线;三是求函数的最大值与最小值;四是求长度、面积、体积和重心等.牛顿(Isaac Newton,1642—1727,英国),被誉为人类历史上最伟大的科学家之一,他创立了微积分,并且构筑了力学的大厦。
物理的尽头是数学,
数学的尽头是哲学. 莱布尼茨(Gottfried Wilhelm Leibniz,1646-1716,德国),是德国最重要的数学家和哲学家,一个举世罕见的科学天才,和牛顿同为微积分的创建人。他所创设的微积分符号远远优于牛顿的符号,这对微积分的发展有极大的影响。
现实背景:注水量与水深的变化问题1:向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图像如右图所示,那么水瓶的形状是( ) B问题2:你吹过气球吗?回忆吹气球的过程
有什么变化现象?这些变化的快慢怎样?随着气球内空气容量的增加,气球的半径增加得越来越慢。你能从数学的角度,描述和解析这种变化快慢的现象吗?吹气球的理想化数学模型随着气球体积的增大,当气球体积增加量相同时,相应半径的增加量越来越小。 能用数量关系来定量解释这个现象吗?增量比你能用数量关系来定量解释这个现象吗?看图说话随着气球体积的增大,当气球体积增加量相同时,相应半径的增加量越来越小。 现实背景:高台跳水问题问题3:(1)请你计算,在 这段时间内运动员的平均速度;(2)请你计算,在 这段时间内运动员的平均速度.问题4:从个别到一般-----
用数学的眼光看问题自变量的改变量函数值的改变量平均变化率是描述变化快慢的 重要指标问题5:物体的平均速度能否精确反映它的运动状态??现实背景:高台跳水问题问题6:问题6—1:2s左右怎样表示?问题6—2:在2s “瞬间”的平均速度是什么? 化简变形“极限”是什么?无穷小量…无穷大…无限接近…逼近…庄子:一尺之棰,日取其半,万世不竭.刘徽的“割圆术”:割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣.基本思想:无限分割,以直代曲.重要意义极限(limit)运动员在某一时刻t0的瞬时速度怎样表示? 瞬时变化率问题7:依照前面的研究,你能给出函数y=f(x)在x=x0处的瞬时变化率的定义吗?这是与x0有关的确定值 ---- 导数体验导数的力量生活中的微积分 由导数的定义,我们知道:
高度 h 关于时间 t 的导数就是运动员
的 ;气球半径 r 关于体积 v 的导数就是气球的 .
牛顿:速度v关于时间t的导数是 .
瞬时速度瞬时膨胀率 实际上,导数可以描述任何事物的变化率,如效率、国内生产总值GDP的增长率,等等.瞬时加速度导数是微积分的核心概念之一微积分是数学中的一门中心学科,是从数学的角度研究变化,在涉及变化的地方,我们总会发现微积分。
历史上有两个伟大的人物牛顿和莱布尼茨对微积分的发展作出了杰出的贡献。
牛顿研究微积分着重于从运动学来考虑,莱布尼茨却是侧重于几何学来考虑。
牛顿建立了无穷小概念,从而奠定了微积分的基础。
课后作业阅读教材第6页例1
完成教材第10页习题1.1第3题
阅读教材第61页“走进微积分”
有兴趣的同学课后可上网查阅有关微积分创建的故事,了解微积分创建的意义和伟大功绩。
数学就是这样一种东西:她提醒你有无形的灵魂,她赋予她所发现的真理以生命;她唤起心神,澄清智慧;她给我们的内心思想增添光辉;她涤尽我们有生以来的蒙昧与无知。——Proclus谢谢!
再见!
