1.1.2 导数的概念课件19张PPT
文档属性
| 名称 | 1.1.2 导数的概念课件19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:33:20 | ||
图片预览





文档简介
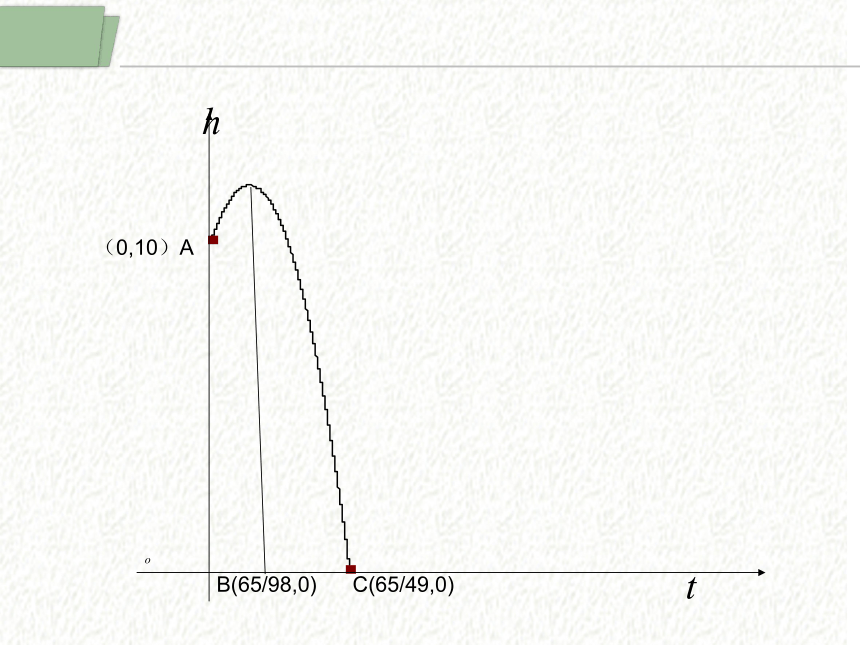
课件19张PPT。导数的概念课堂回忆1、平均变化率概念: 2、平均变化率的几何意义:表示某一点的割线斜率3、平均变化率求法:称为函数f(x)从 到 的平均变化率 (1)求增量:(2)求平均变化率学习目标理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵 ;会求函数在某点的导数.探究:高台跳水问题新课引入在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)= -4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态?吴敏霞科比(0,10)AB(65/98,0)C(65/49,0)探究(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有什么
问题吗?平均速度不能反映他在这段时间里运动状态,需要用
瞬时速度描述运动状态。 2.瞬时速度我们把物体在某一时刻的速度称为瞬时速度。运动员的平均速度不能反映他在某一时刻的瞬时速度,那么,如何求运动员的瞬时速度呢?比如,t=2时的瞬时速度是多少?考察t=2时附近的情况:如下图所示 感悟体验t=2.5附近的平均速度变化:t=3附近的平均速度变化:那如何求函数在某一点处的瞬时变化率呢?把Δx区间缩短概念形成定义:函数 y = f (x) 在 x = x0 处的瞬时变化率是称为函数 y = f (x) 在 x = x0 处的导数, 记作或 , 即导数是一种形式定义注意:瞬时变化率和导数是同一个概念的两个名称在数学中,如果某个变化的量无限地逼近于一个确定的数值,那么该定值就叫做变化的量的极限.割线的极限位置概念拓展播放例题分析 求函数y=2x2+4x在x=3处的导数. 变式B课堂小结
1. 瞬时速度的概念
2.导数的概念
3.求导数的步骤是什么?谢谢大家!
(2)你认为用平均速度描述运动员的运动状态有什么
问题吗?平均速度不能反映他在这段时间里运动状态,需要用
瞬时速度描述运动状态。 2.瞬时速度我们把物体在某一时刻的速度称为瞬时速度。运动员的平均速度不能反映他在某一时刻的瞬时速度,那么,如何求运动员的瞬时速度呢?比如,t=2时的瞬时速度是多少?考察t=2时附近的情况:如下图所示 感悟体验t=2.5附近的平均速度变化:t=3附近的平均速度变化:那如何求函数在某一点处的瞬时变化率呢?把Δx区间缩短概念形成定义:函数 y = f (x) 在 x = x0 处的瞬时变化率是称为函数 y = f (x) 在 x = x0 处的导数, 记作或 , 即导数是一种形式定义注意:瞬时变化率和导数是同一个概念的两个名称在数学中,如果某个变化的量无限地逼近于一个确定的数值,那么该定值就叫做变化的量的极限.割线的极限位置概念拓展播放例题分析 求函数y=2x2+4x在x=3处的导数. 变式B课堂小结
1. 瞬时速度的概念
2.导数的概念
3.求导数的步骤是什么?谢谢大家!
