1.1.2 导数的概念课件19张PPT
文档属性
| 名称 | 1.1.2 导数的概念课件19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:32:57 | ||
图片预览






文档简介
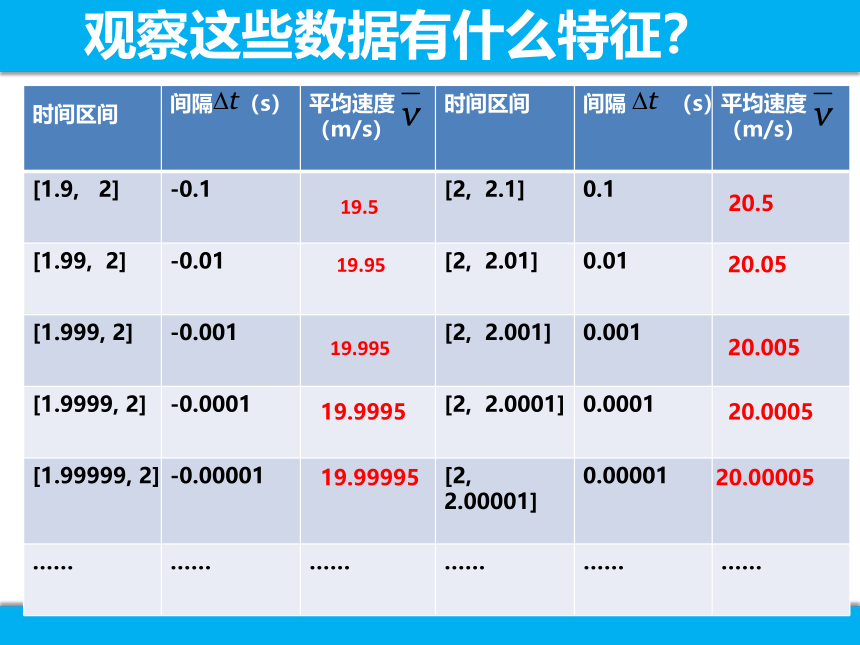
课件19张PPT。1.1.2导数的概念课前任务: 阅读课本第61-62页实习作业《走进微积分》,同学们阅读课本,并上网查阅牛顿,莱布尼茨生平简介,以及他们创立微积分的起始问题是什么?有何差异?一、求运动物体的瞬时速度观察这些数据有什么特征?小组讨论:1、当 趋近于0时,平均速度 有什么样的变化趋势?2、运动物体在2s时刻的瞬时速度是多少?理由是什么?用数学式子表示这个过程.3、运动物体在 时刻的瞬时速度怎样表示?二、求切线的斜率例2、求抛物线 在点
处的切线方程。 初中我们是怎么定义圆的切线的?观察:图中的虚线是曲线的切线吗?观察:图中的直线是曲线的切线吗? 思考:1、通过割线变切线的方法,有一般性吗?
能用来求其它切线的斜率吗?
2、仿照求瞬时速度的思路和方法,用数学式子表示这一过程。利用割线求切线利用割线求切线利用割线变切线的思路,求
抛物线 在点 处的
切线方程。 练习1:利用割线求切线的过程: 练习2:将原油精炼为汽油、柴油、塑胶
等各种不同产品,需要对原油进
行冷却和加热,如果在第 h时,
原油的温度(单位℃ )为
计算第2h
与第6h时,原油温度的瞬时变化率,并说明它们的意义。分析:在第 2h 和第6h时,原油温度的瞬时变化率就是解:所以,同理可得 它说明在第2h附近,原油温度大约以 的速率 ;
它说明在第6h附近,原油温度大约以 的速率 。
一般的, 反映了原油温度在 时刻附近的变化情况。求的值求导步骤求平均
变化率取极限5 上升53下降 作业:
完成《导数的概念》固学案
处的切线方程。 初中我们是怎么定义圆的切线的?观察:图中的虚线是曲线的切线吗?观察:图中的直线是曲线的切线吗? 思考:1、通过割线变切线的方法,有一般性吗?
能用来求其它切线的斜率吗?
2、仿照求瞬时速度的思路和方法,用数学式子表示这一过程。利用割线求切线利用割线求切线利用割线变切线的思路,求
抛物线 在点 处的
切线方程。 练习1:利用割线求切线的过程: 练习2:将原油精炼为汽油、柴油、塑胶
等各种不同产品,需要对原油进
行冷却和加热,如果在第 h时,
原油的温度(单位℃ )为
计算第2h
与第6h时,原油温度的瞬时变化率,并说明它们的意义。分析:在第 2h 和第6h时,原油温度的瞬时变化率就是解:所以,同理可得 它说明在第2h附近,原油温度大约以 的速率 ;
它说明在第6h附近,原油温度大约以 的速率 。
一般的, 反映了原油温度在 时刻附近的变化情况。求的值求导步骤求平均
变化率取极限5 上升53下降 作业:
完成《导数的概念》固学案
