1.2.2 基本初等函数的导数公式及导数的运算法则课件25张PPT?
文档属性
| 名称 | 1.2.2 基本初等函数的导数公式及导数的运算法则课件25张PPT? |

|
|
| 格式 | zip | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 00:00:00 | ||
图片预览








文档简介
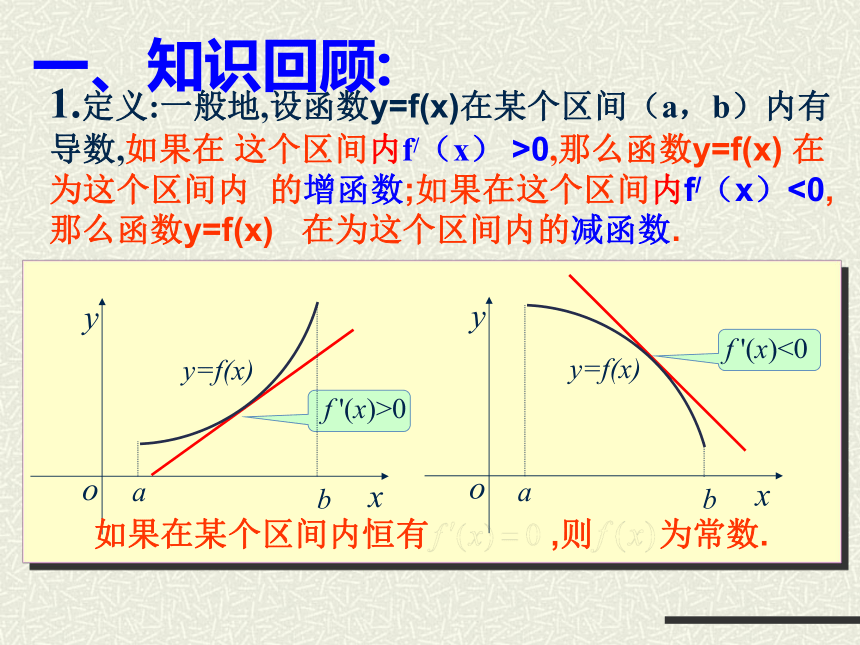
课件25张PPT。 利用导数研究函数的极值、最值 f '(x)>0f '(x)<01.定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,如果在 这个区间内f/(x) >0,那么函数y=f(x) 在为这个区间内 的增函数;如果在这个区间内f/(x)<0,那么函数y=f(x) 在为这个区间内的减函数.一、知识回顾:2.求函数单调性的一般步骤①求函数的定义域;②求函数的导数 f/(x); ③解不等式 f/(x)>0 得f(x)的单调
递增区间;
解不等式 f/(x)<0 得f(x)的单调递减区间.定义域为R时可省二、新课讲解——函数的极值: 1. 观察右下图为函数y=2x3-6x2+7的图象,从图象我们可以看出下面的结论: 函数在X=0的函数值比它附近所有各点的函数值都大,这时我们说f(0)是函数的一个极大值;0是函数 的一个极大值点。函数在X=2的函数值比它附近所有各点的函数值都小,我们说f(2)是函数的一个极小值, 2是函数 的一个极小值点。y0 如图,函数 y=f(x)在x1,x2,x3,x4等点的 函数值与这些点附近的函数值有什么关系?
Y=f(x)在这些点的导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律?2.探索思考: 从而我们得出结论: 若x0满足 f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值点,f(x0)是极值,并且如果 f/(x) 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 f/(x) 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值.极大值与极小值统称为极值. 从曲线的切线角度看,曲线在极值点处切线的斜率为0,并且,曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正.三、例题选讲:例1:求y=x3/3-4x+4的极值.因此,当x=-2时有极大值,并且,y极大值=28/3;
而,当x=2时有极小值,并且,y极小值=- 4/3.四.探索思考: 导数值为0的点一定是函数的极值点吗? 可导函数的极值点一定是它导数为零的点,反之函数的导数为零的点,不一定是该函数的极值点.例如,函数y=x3,在点x=0处的导数为零,但它不是极值点,原因是函数在点x=0处左右两侧的导数都大于零. 因此导数为零的点仅是该点为极值点的必要条件,其充分条件是在这点两侧的导数异号.
一般地,求函数y=f(x)的极值的方法是: (1):如果在x0附近的左侧 f/(x)>0 右侧 f/(x)<0 , 那么f(x0)是极大值; (2):如果在x0附近的左侧 f/(x)<0 右侧 f/(x)>0 , 那么f(x0)是极小值.解方程f/(x)=0.当f/(x)=0时:故当x=-a时,f(x)有极大值f(-a)=-2a;当x=a时,f(x)有极小值f(a)=2a.因此,当x=-1时有极大值,并且,y极大值=3;
而,当x=1时有极小值,并且,y极小值=- 3.由于g(0)=-1≤0,故只需g(1)=2-2a≤0,即a≥1.所以,a≥1是k≥-1成立的充要条件. (1)设a>0,列表如下:又5a=3b,解得a=3,b=5,c=2.(2)设a<0,列表如下:又5a=3b,解得a=-3,b=-5,c=2.练习1:已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为
10,求a、b的值.又f(1)=10,故1+a+b+a2=10.②从而所求的解为a=4,b=-11.再见 第二课时一、复习:1.设函数y=f(x)在x0及其附近有定义,如果f(x0)的值比x0
附近所有各点的函数值都大,我们说f(x0)是函数y=f(x)
的一个极大值;如果f(x0)的值比x0附近所有各点的函
数值都小,我们说f(x0)是函数y=f(x)的一个极小值.极
大值与极小值统称极值.2.当函数f(x)在x0处连续时,判别f(x0)是极大(小)值的方
法是:3.理解函数极值的定义时应注意以下几点:(1)函数的极值是一个局部性的概念,极值点是区间内
部的点而不会是端点.(2)若f(x)在某区间内有极值,那么f(x)在某区间内一定
不是单调函数,即在区间上单调的函数没有极值.(3)极大值与极小值没有必然的大小关系,即极大值不
一定比极小值大,极小值不一定比极大值小.(4)函数f(x)在某区间内有极值,它的极值点的分布是
有规律的,相邻两个极大值点之间必有一个极小值
点,同样相邻两个极小值点之间必有一个极大值点.
一般地,当函数f(x)在某区间上连续且有有限极值
点时,函数f(x)在该区间内的极大值点与极小值点
是交替出现的.(5)导数为零的点是该点为极值点的必要条件,而不是
充分条件.(6)极值只能在函数不可导的点或导数为零的点取到.4.确定函数的极值应从几何直观入手,理解可导函数在
其定义域上的单调性与函数极值的相互关系,掌握利
用导数判断函数极值的基本方法.为什么要加上这一步?又设g(x)=-ax2-2bx+a, 由于-a<0,g(x)的图象开口
向下,g(x)的值在α的右正左负,在β的左正右负.两式相加,并注意到α+β=-2b/a,于是有:故所求的值为a=2,b=0.关注用导数本质及其几何意义解决问题 3.思考: 观察下图,当t=t0时距水面的高度最大,那么函数 h(t)在此点的导数是多少呢?此点附近的图象有什么特点?相应地,导数的符号有什么变化规律?
递增区间;
解不等式 f/(x)<0 得f(x)的单调递减区间.定义域为R时可省二、新课讲解——函数的极值: 1. 观察右下图为函数y=2x3-6x2+7的图象,从图象我们可以看出下面的结论: 函数在X=0的函数值比它附近所有各点的函数值都大,这时我们说f(0)是函数的一个极大值;0是函数 的一个极大值点。函数在X=2的函数值比它附近所有各点的函数值都小,我们说f(2)是函数的一个极小值, 2是函数 的一个极小值点。y0 如图,函数 y=f(x)在x1,x2,x3,x4等点的 函数值与这些点附近的函数值有什么关系?
Y=f(x)在这些点的导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律?2.探索思考: 从而我们得出结论: 若x0满足 f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值点,f(x0)是极值,并且如果 f/(x) 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 f/(x) 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值.极大值与极小值统称为极值. 从曲线的切线角度看,曲线在极值点处切线的斜率为0,并且,曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正.三、例题选讲:例1:求y=x3/3-4x+4的极值.因此,当x=-2时有极大值,并且,y极大值=28/3;
而,当x=2时有极小值,并且,y极小值=- 4/3.四.探索思考: 导数值为0的点一定是函数的极值点吗? 可导函数的极值点一定是它导数为零的点,反之函数的导数为零的点,不一定是该函数的极值点.例如,函数y=x3,在点x=0处的导数为零,但它不是极值点,原因是函数在点x=0处左右两侧的导数都大于零. 因此导数为零的点仅是该点为极值点的必要条件,其充分条件是在这点两侧的导数异号.
一般地,求函数y=f(x)的极值的方法是: (1):如果在x0附近的左侧 f/(x)>0 右侧 f/(x)<0 , 那么f(x0)是极大值; (2):如果在x0附近的左侧 f/(x)<0 右侧 f/(x)>0 , 那么f(x0)是极小值.解方程f/(x)=0.当f/(x)=0时:故当x=-a时,f(x)有极大值f(-a)=-2a;当x=a时,f(x)有极小值f(a)=2a.因此,当x=-1时有极大值,并且,y极大值=3;
而,当x=1时有极小值,并且,y极小值=- 3.由于g(0)=-1≤0,故只需g(1)=2-2a≤0,即a≥1.所以,a≥1是k≥-1成立的充要条件. (1)设a>0,列表如下:又5a=3b,解得a=3,b=5,c=2.(2)设a<0,列表如下:又5a=3b,解得a=-3,b=-5,c=2.练习1:已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为
10,求a、b的值.又f(1)=10,故1+a+b+a2=10.②从而所求的解为a=4,b=-11.再见 第二课时一、复习:1.设函数y=f(x)在x0及其附近有定义,如果f(x0)的值比x0
附近所有各点的函数值都大,我们说f(x0)是函数y=f(x)
的一个极大值;如果f(x0)的值比x0附近所有各点的函
数值都小,我们说f(x0)是函数y=f(x)的一个极小值.极
大值与极小值统称极值.2.当函数f(x)在x0处连续时,判别f(x0)是极大(小)值的方
法是:3.理解函数极值的定义时应注意以下几点:(1)函数的极值是一个局部性的概念,极值点是区间内
部的点而不会是端点.(2)若f(x)在某区间内有极值,那么f(x)在某区间内一定
不是单调函数,即在区间上单调的函数没有极值.(3)极大值与极小值没有必然的大小关系,即极大值不
一定比极小值大,极小值不一定比极大值小.(4)函数f(x)在某区间内有极值,它的极值点的分布是
有规律的,相邻两个极大值点之间必有一个极小值
点,同样相邻两个极小值点之间必有一个极大值点.
一般地,当函数f(x)在某区间上连续且有有限极值
点时,函数f(x)在该区间内的极大值点与极小值点
是交替出现的.(5)导数为零的点是该点为极值点的必要条件,而不是
充分条件.(6)极值只能在函数不可导的点或导数为零的点取到.4.确定函数的极值应从几何直观入手,理解可导函数在
其定义域上的单调性与函数极值的相互关系,掌握利
用导数判断函数极值的基本方法.为什么要加上这一步?又设g(x)=-ax2-2bx+a, 由于-a<0,g(x)的图象开口
向下,g(x)的值在α的右正左负,在β的左正右负.两式相加,并注意到α+β=-2b/a,于是有:故所求的值为a=2,b=0.关注用导数本质及其几何意义解决问题 3.思考: 观察下图,当t=t0时距水面的高度最大,那么函数 h(t)在此点的导数是多少呢?此点附近的图象有什么特点?相应地,导数的符号有什么变化规律?
