1.2 函数的单调性与导数课件23张PPT
文档属性
| 名称 | 1.2 函数的单调性与导数课件23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 958.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 00:00:00 | ||
图片预览







文档简介
课件23张PPT。1.3.1函数的单调性与导数 如图(1)表示高台跳水运动
员的高度 h 随时间 t 变化的
函数 的图象, 图(2)表示高台跳水
运动员的速度 v 随时间 t 变
化的函数 的图象.运动员从起跳到最高
点, 以及从最高点到入水这两
段时间的运动状态有什么区别?aabbttvhOO(1)(2)探究点:函数的单调性与其导函数的关系(1)(2)aabbttvhOO①运动员从起跳到最高点,离水面的高度h随时间t 的增
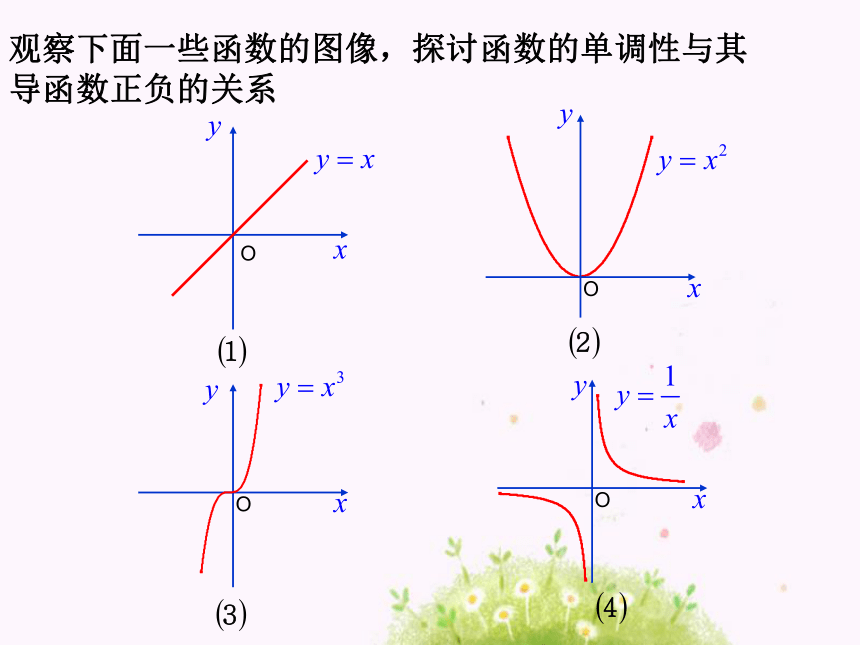
加而增加,即h(t)是增函数.相应地,(1)(2)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(1)中的函数y=x的导函数y′=__,此函数的单调增
区间为__________;1(-∞,+∞)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(2)中的函数y=x2的导函数y′=___,此函数的单调
增区间为________;单调减区间为________;2x(0,+∞)(-∞,0)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(3)中的函数y=x3的导函数y′=___,此函数的单调
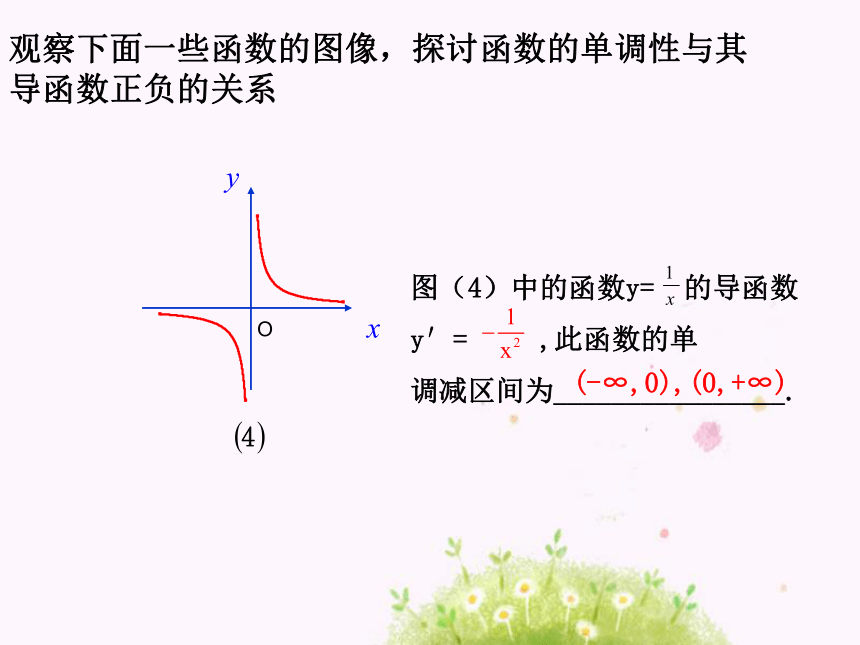
增区间为_________;3x2(-∞,+∞)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系(-∞,0),(0,+∞)根据刚才的观察,思考函数的单调性与导函数的正负有什么关系?思考:
(1)在区间(a,b)上,如果f′(x)>0,则f(x)在该区间上单调递增,反过来也成立吗?
不一定成立.例如,f(x)=x3在R上为增函数,但f′(0)=0,即f′(x)>0是f(x)在该区间上单调递增的充分不必要条件.
在区间(a,b)上,如果f′(x)<0,则f(x)在该区间上单调
递减,反过来也不一定成立
(2)利用导数求函数单调区间时,能否忽视定义域?
需要确定函数的定义域,函数的单调区间是定义域的子集.说明:
(1)端点值:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(2)符号:如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
.典例精讲y=f(x)图像唯一吗?例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.你还有没有别的方法?.根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调递增区间;
解不等式f′(x)<0,得函数单调递减区间.【总结】运用函数单调性的定义,能否求解刚才的题目?(-2,0) (-∞,-2),(0,+∞) 【变式练习】2.求可导函数f(x)单调区间的步骤知识小结思想方法小结数形结合函数的单调性与导数1、函数图像的草图【作业布置】课本P26、1、2、3、4题
员的高度 h 随时间 t 变化的
函数 的图象, 图(2)表示高台跳水
运动员的速度 v 随时间 t 变
化的函数 的图象.运动员从起跳到最高
点, 以及从最高点到入水这两
段时间的运动状态有什么区别?aabbttvhOO(1)(2)探究点:函数的单调性与其导函数的关系(1)(2)aabbttvhOO①运动员从起跳到最高点,离水面的高度h随时间t 的增
加而增加,即h(t)是增函数.相应地,(1)(2)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(1)中的函数y=x的导函数y′=__,此函数的单调增
区间为__________;1(-∞,+∞)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(2)中的函数y=x2的导函数y′=___,此函数的单调
增区间为________;单调减区间为________;2x(0,+∞)(-∞,0)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系图(3)中的函数y=x3的导函数y′=___,此函数的单调
增区间为_________;3x2(-∞,+∞)观察下面一些函数的图像,探讨函数的单调性与其
导函数正负的关系(-∞,0),(0,+∞)根据刚才的观察,思考函数的单调性与导函数的正负有什么关系?思考:
(1)在区间(a,b)上,如果f′(x)>0,则f(x)在该区间上单调递增,反过来也成立吗?
不一定成立.例如,f(x)=x3在R上为增函数,但f′(0)=0,即f′(x)>0是f(x)在该区间上单调递增的充分不必要条件.
在区间(a,b)上,如果f′(x)<0,则f(x)在该区间上单调
递减,反过来也不一定成立
(2)利用导数求函数单调区间时,能否忽视定义域?
需要确定函数的定义域,函数的单调区间是定义域的子集.说明:
(1)端点值:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(2)符号:如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
.典例精讲y=f(x)图像唯一吗?例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.你还有没有别的方法?.根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调递增区间;
解不等式f′(x)<0,得函数单调递减区间.【总结】运用函数单调性的定义,能否求解刚才的题目?(-2,0) (-∞,-2),(0,+∞) 【变式练习】2.求可导函数f(x)单调区间的步骤知识小结思想方法小结数形结合函数的单调性与导数1、函数图像的草图【作业布置】课本P26、1、2、3、4题
