3.1基本初等函数的导数公式及导数的运算法则课件22张PPT
文档属性
| 名称 | 3.1基本初等函数的导数公式及导数的运算法则课件22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 644.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:38:16 | ||
图片预览






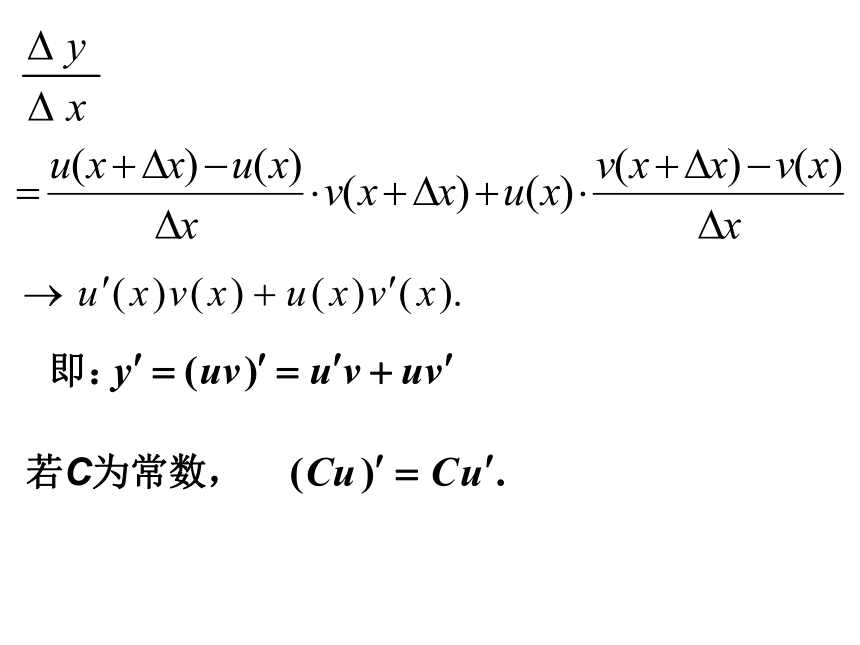
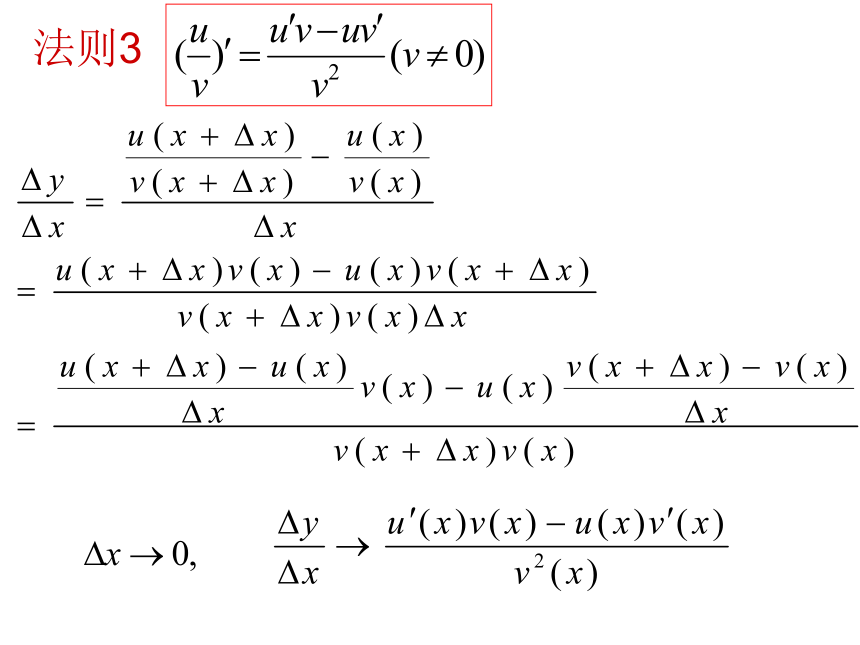

文档简介
课件22张PPT。3.2.2基本初等函数的导数公式及导数的运算法则高二数学 选修1-1 第三章 导数及其应用可以直接使用的基本初等函数的导数公式可以直接使用的基本初等函数的导数公式导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:由法则2:若C为常数, 法则3例2:求下列函数的导数:题型一:导数公式及导数运算法则的应用题型二:导数的综合应用例6.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均
相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4.解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得:
t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在
始点.故在t=0,t=4和t=8秒时物体运动的速度为零.
相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4.解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得:
t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在
始点.故在t=0,t=4和t=8秒时物体运动的速度为零.
