基于曲线切割线斜率关系的不等式研究课件16张PPT
文档属性
| 名称 | 基于曲线切割线斜率关系的不等式研究课件16张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 20:37:08 | ||
图片预览






文档简介
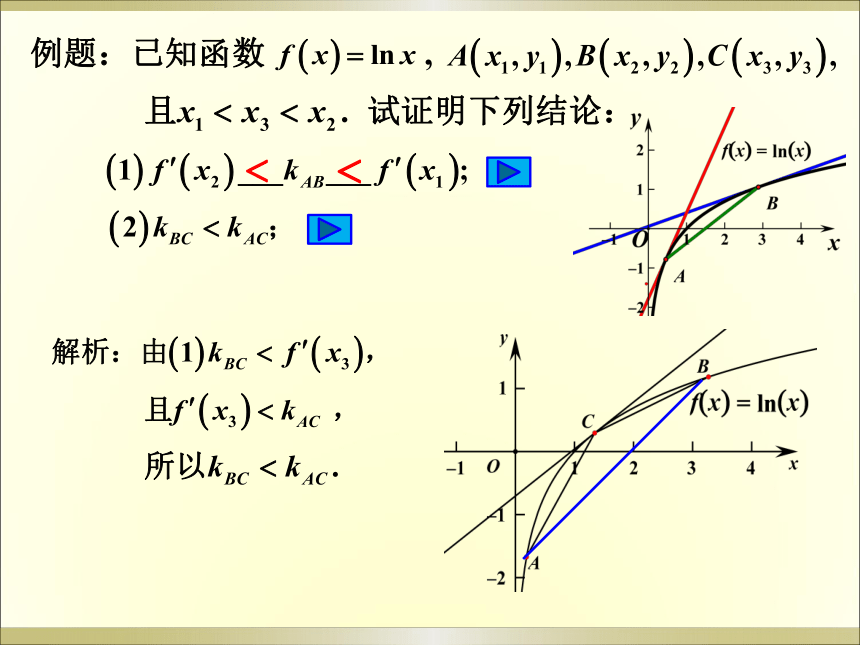
课件16张PPT。基于曲线切割线斜率关系的
不等式研究例题:已知函数 ,试证明下列结论:例题:已知函数 ,试证明下列结论:问题1:几何意义是什么?问题2:还可以等价转化成什么问题?①②(3)分析:由零点存在定理,证明:例题:已知函数 ,试证明下列结论:例题:已知函数 ,试证明下列结论:证明:原不等式转化为小结(一):对数型双元不等式题型特征及证明策略转化为含有 或 的不等式;换元(令 或 );把待证的不等式等价转化为关于 t 的不等式;构造关于t的函数 g(t) ;利用导数求解 g(t) 的最值,从而证明不等式。
(比值换元,构造新函数)解题流程:二元一元待证的不等式含有对数式等,当x1=x2时,原不等式一端分式为 型,或 或
左端=右端等形式.法二:原不等式成立.由 x1 < x2 ,构造以 x1为参数,以 x2为 自变量的函数.主元法二元一元小结(二)主元法证明对数型二元不等式解题流程: 利用导数求解 g(x) 的最值,从而证明不等式。 将其一变量当作已知范围内参数,
另一个变量作为自变量构造函数g (x) ;对比比值换元法,主元法的优缺点:优点:不用技巧,直接将待证不等式简单变形,
构造新函数;缺点:有时计算麻烦.例题:已知函数 ,试证明下列结论:对数平均值不等式:例题:已知函数 ,试证明下列结论:例2.(2017年宁德第一次市质检)(2) 若 是曲线
上的两点, .问: 是否存在 ,使得直线 的斜
率等于 ?若存在 ,求出 ;若不存在,说明理由.已知函数分析:例2.(2017年宁德第一次市质检)(2) 若 是曲线
上的两点, .问: 是否存在 ,使得直线 的斜
率等于 ?若存在 ,求出 ;若不存在,说明理由.已知函数分析:课堂小结:(一)重要不等式:(二)对数型双元不等式证法:2.主元法,构造新函数.1.比值换元 ,构造新函数;二元一元减元2.对数平均值不等式:1. x - 1 ≥ lnx思考题:指数函数 与对数函数 互为反函数,它们有很多类似的性质,能否类比研究对数函数
图像的切割线斜率关系来研究指数函数的呢?
可以得到哪些结论?怎么证明?
试写出解题策略流程.故原不等式成立.法一:由 x1 < x2 ,证明:由 x1 < x2 ,构造以 x1为参数,以 x2为 自变量的函数.故原不等式成立.
(比值换元,构造新函数)解题流程:二元一元待证的不等式含有对数式等,当x1=x2时,原不等式一端分式为 型,或 或
左端=右端等形式.法二:原不等式成立.由 x1 < x2 ,构造以 x1为参数,以 x2为 自变量的函数.主元法二元一元小结(二)主元法证明对数型二元不等式解题流程: 利用导数求解 g(x) 的最值,从而证明不等式。 将其一变量当作已知范围内参数,
另一个变量作为自变量构造函数g (x) ;对比比值换元法,主元法的优缺点:优点:不用技巧,直接将待证不等式简单变形,
构造新函数;缺点:有时计算麻烦.例题:已知函数 ,试证明下列结论:对数平均值不等式:例题:已知函数 ,试证明下列结论:例2.(2017年宁德第一次市质检)(2) 若 是曲线
上的两点, .问: 是否存在 ,使得直线 的斜
率等于 ?若存在 ,求出 ;若不存在,说明理由.已知函数分析:例2.(2017年宁德第一次市质检)(2) 若 是曲线
上的两点, .问: 是否存在 ,使得直线 的斜
率等于 ?若存在 ,求出 ;若不存在,说明理由.已知函数分析:课堂小结:(一)重要不等式:(二)对数型双元不等式证法:2.主元法,构造新函数.1.比值换元 ,构造新函数;二元一元减元2.对数平均值不等式:1. x - 1 ≥ lnx思考题:指数函数 与对数函数 互为反函数,它们有很多类似的性质,能否类比研究对数函数
图像的切割线斜率关系来研究指数函数的呢?
可以得到哪些结论?怎么证明?
试写出解题策略流程.故原不等式成立.法一:由 x1 < x2 ,证明:由 x1 < x2 ,构造以 x1为参数,以 x2为 自变量的函数.故原不等式成立.
