选修3-1 第六讲 近代数学两巨星 分析的化身──欧拉课件32张PPT
文档属性
| 名称 | 选修3-1 第六讲 近代数学两巨星 分析的化身──欧拉课件32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-14 00:00:00 | ||
图片预览









文档简介
课件32张PPT。所有人的老师分析的化身—欧拉 1.数学英雄:
欧拉(Leonhard Euler公元1707 -1783年) ,瑞士数学家,13岁进巴 塞尔大学读书,得到著名数学家贝努 利的精心指导.欧拉是科学史上最多 产的一位杰出的数学家,他从19岁开 始发表论文,直到76岁,在他那不倦 的一生中,共写下了886本书籍和论文,
其中在世时发表了700多篇论文。 彼得堡科学院为了整理他的著作,整 整用了47年。
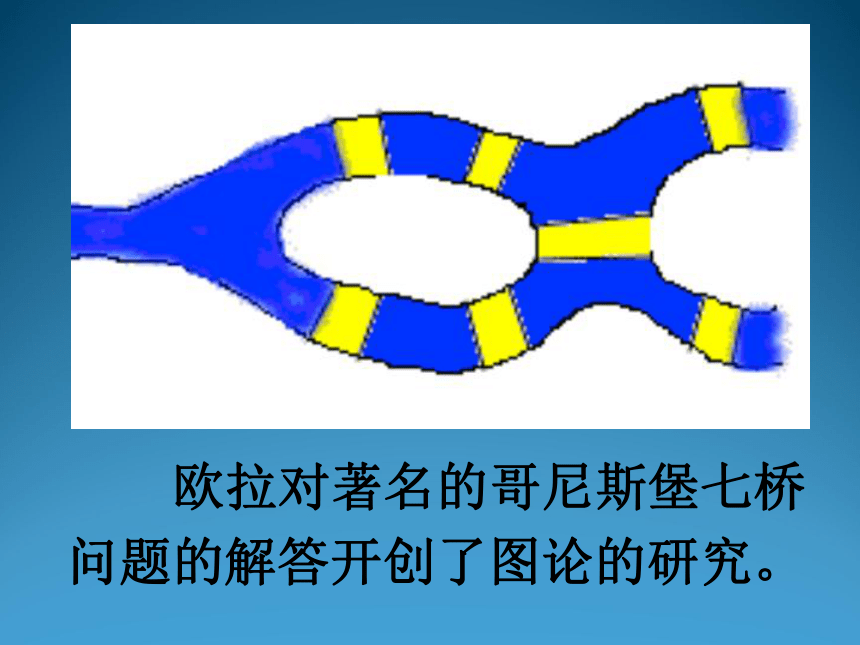
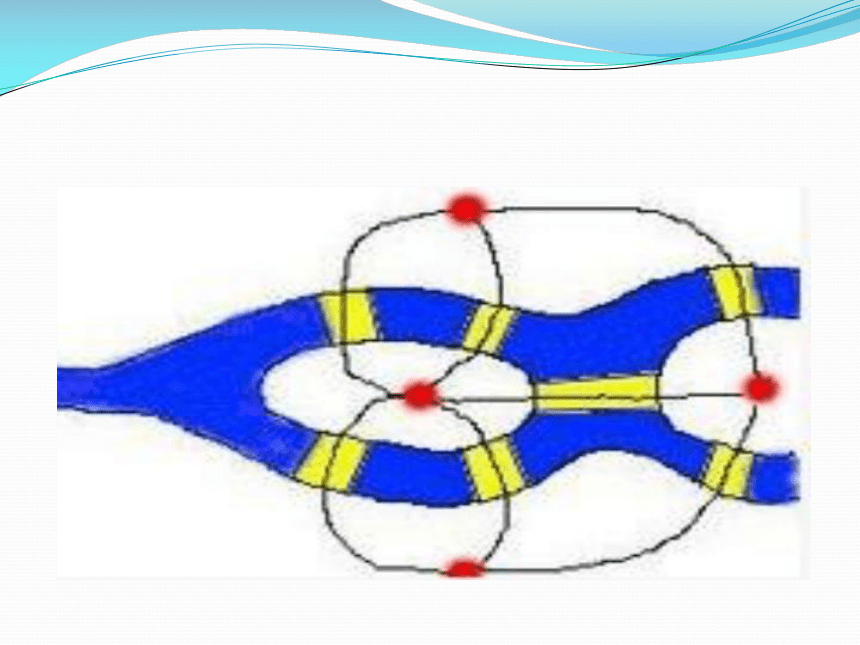
他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。欧拉对数学的研究如此之广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。2.欧拉的丰功伟绩2.欧拉的丰功伟绩图论起源于18世纪,1736年瑞士数学家欧拉(Euler)发表了图论的第一篇论文“哥尼斯堡七桥问题”。在当时的哥尼斯堡城有一条横贯全市的普雷格尔河,河中的两个岛与两岸用七座桥连结起来。当时那里的居民热衷于一个难题:有游人怎样不重复地走遍七桥,最后回到出发点。 欧拉对著名的哥尼斯堡七桥 问题的解答开创了图论的研究。 为了解决这个问题,欧拉用 A,B,C,D 4个字母代替陆地,作为 4 个顶点,将联结两块陆地的桥用相应的线段表示,于是哥尼斯堡七桥问题就变成了图中,是否存在经过每条边一次且仅一次,经过所有的顶点的回路问题了。欧拉在论文中指出,这样的回路是不存在的。 欧拉发现对任何凸多面体, 其顶点数V、棱数E、面数F之间 总有 V-E+F=2 这个关系。 V-E+F 被称为欧拉示性数, 成为拓扑学的基础概念。 简单多面体最有趣的定理之一
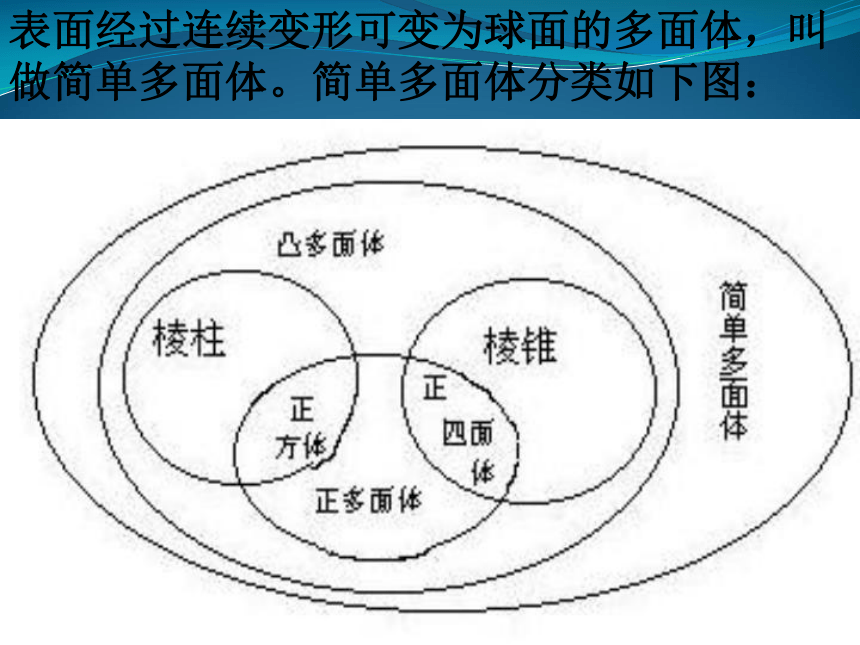
欧拉公式:V-E+F=2其中 V(Vertex)是多面体的顶点数,E(Edge)是棱数,F(Face)是面数也称欧拉示性数什么叫做正多面体?世界上有多少种正多面体?表面经过连续变形可变为球面的多面体,叫做简单多面体。简单多面体分类如下图: 用欧拉公式V-E+F=2证明:正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。用欧拉公式证明正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。证:对于正多面体,假设它的各面都是正n边形,而且每一个顶角处有m 条边相遇。这样就有:
nF=2E (1)
mV=2E (2)(1)的右边系数2是因为每边(棱)出现在2个面中, (2)的右边系数2是因为每边通过2个顶角. 把(1)和(2)代入欧拉公式中,就得到:
????????????????显然n≥3,m≥3 但n>3,且m>3又是不可能的 因此m=3,4,5, 所以E=6,12,30, 从而F =4,8,20, 这就给出了正四面体、正八面体 和正二十面体. 因此n=3,4,5,
所以E=6,12,30,
从而F=4,6,12, 这就给出了正四面体、正六面 体(即立方体)和正十二面体.知道圆周率吗?谁能够说出圆周率的全部数据?3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387538865875332083814206171776691473045982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303欧拉创设了许多数学符号,例如π(1736年)e(1748年)i(1777年)sin和cos(1748年)tg(1753年)△x(1755年)Σ(1755年)f(x)(1734年) 欧拉最先把对数定义为乘方的逆 运算,并且最先发现了对数是无穷多 值的。他证明了任一非零实数R有无 穷多个对数。欧拉使三角学成为一门 系统的科学,他首先用比值来给出三 角函数的定义,而在他以前是一直以 线段的长作为定义的。欧拉的定义使 三角学跳出只研究三角表这个圈子。 欧拉对整个三角学作了分析性的研究。最优美的数学公式 1774年,欧拉把自己多年来 研究变分问题所取得的成果集中 发表在一本书《寻求具有某种极 大或极小性质的曲线的技巧》中。欧拉从而创立了一个新的数学分 支──变分法 欧拉研究了天文学,并与 达朗贝尔及拉格朗日一起成为 天体力学的创立者 。 欧拉研究了流体的运动性质,建立了理想流体运动的基 本微分方程 ,成为流体力学的 创始人。 欧拉把自己所建立的理想流体运动的基本方程用于人体血液的流动,从而在生物学上添上了他的贡献,又以流体力学、潮汐理论为基础,丰富和发展了船舶设计制造及航海理论。 1783年9月18日下午,欧拉一边和小孙女逗着玩,一边思考着计算天王星的轨迹,突然,他从椅子上滑下来,嘴里轻声说:“我死了”。一位科学巨匠就这样停止了生命。 欧拉从19岁开始写作,直到逝世,留下了浩如烟海的论文、著作,甚至在他死后,他留下的许多手稿还丰富了后47年的圣彼得堡科学院学报。就科研成果方面来说,欧拉是数学史上或者说是自然科学史上首屈一指的。 历史学家把欧拉和阿基米德、牛顿、高斯列为有史以来贡献最大的四位数学家,依据是他们都有一个共同点,就是在创建纯粹理论的同时,还应用这些数学工具去解决大量天文、物理和力学等方面的实际问题,他们的工作是跨学科的,他们不断地从实践中吸取丰富的营养,但又不满足于具体问题的解决,而是把宇宙看作是一个有机的整体,力图揭示它的奥秘和内在规律。 法国数学家拉普拉斯则认为:读读欧拉,他是所有人的老师。瑞士教育与研究国务秘书Charles Kleiber曾表示:“没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活。惊叹欧拉 丰功伟绩;钦佩
欧拉坚持不懈的治学 精神;学习欧拉 思想和方法.祝同学们在新的学期里
更高,更快,更强
欧拉(Leonhard Euler公元1707 -1783年) ,瑞士数学家,13岁进巴 塞尔大学读书,得到著名数学家贝努 利的精心指导.欧拉是科学史上最多 产的一位杰出的数学家,他从19岁开 始发表论文,直到76岁,在他那不倦 的一生中,共写下了886本书籍和论文,
其中在世时发表了700多篇论文。 彼得堡科学院为了整理他的著作,整 整用了47年。
他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。欧拉对数学的研究如此之广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。2.欧拉的丰功伟绩2.欧拉的丰功伟绩图论起源于18世纪,1736年瑞士数学家欧拉(Euler)发表了图论的第一篇论文“哥尼斯堡七桥问题”。在当时的哥尼斯堡城有一条横贯全市的普雷格尔河,河中的两个岛与两岸用七座桥连结起来。当时那里的居民热衷于一个难题:有游人怎样不重复地走遍七桥,最后回到出发点。 欧拉对著名的哥尼斯堡七桥 问题的解答开创了图论的研究。 为了解决这个问题,欧拉用 A,B,C,D 4个字母代替陆地,作为 4 个顶点,将联结两块陆地的桥用相应的线段表示,于是哥尼斯堡七桥问题就变成了图中,是否存在经过每条边一次且仅一次,经过所有的顶点的回路问题了。欧拉在论文中指出,这样的回路是不存在的。 欧拉发现对任何凸多面体, 其顶点数V、棱数E、面数F之间 总有 V-E+F=2 这个关系。 V-E+F 被称为欧拉示性数, 成为拓扑学的基础概念。 简单多面体最有趣的定理之一
欧拉公式:V-E+F=2其中 V(Vertex)是多面体的顶点数,E(Edge)是棱数,F(Face)是面数也称欧拉示性数什么叫做正多面体?世界上有多少种正多面体?表面经过连续变形可变为球面的多面体,叫做简单多面体。简单多面体分类如下图: 用欧拉公式V-E+F=2证明:正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。用欧拉公式证明正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。证:对于正多面体,假设它的各面都是正n边形,而且每一个顶角处有m 条边相遇。这样就有:
nF=2E (1)
mV=2E (2)(1)的右边系数2是因为每边(棱)出现在2个面中, (2)的右边系数2是因为每边通过2个顶角. 把(1)和(2)代入欧拉公式中,就得到:
????????????????显然n≥3,m≥3 但n>3,且m>3又是不可能的 因此m=3,4,5, 所以E=6,12,30, 从而F =4,8,20, 这就给出了正四面体、正八面体 和正二十面体. 因此n=3,4,5,
所以E=6,12,30,
从而F=4,6,12, 这就给出了正四面体、正六面 体(即立方体)和正十二面体.知道圆周率吗?谁能够说出圆周率的全部数据?3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387538865875332083814206171776691473045982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303欧拉创设了许多数学符号,例如π(1736年)e(1748年)i(1777年)sin和cos(1748年)tg(1753年)△x(1755年)Σ(1755年)f(x)(1734年) 欧拉最先把对数定义为乘方的逆 运算,并且最先发现了对数是无穷多 值的。他证明了任一非零实数R有无 穷多个对数。欧拉使三角学成为一门 系统的科学,他首先用比值来给出三 角函数的定义,而在他以前是一直以 线段的长作为定义的。欧拉的定义使 三角学跳出只研究三角表这个圈子。 欧拉对整个三角学作了分析性的研究。最优美的数学公式 1774年,欧拉把自己多年来 研究变分问题所取得的成果集中 发表在一本书《寻求具有某种极 大或极小性质的曲线的技巧》中。欧拉从而创立了一个新的数学分 支──变分法 欧拉研究了天文学,并与 达朗贝尔及拉格朗日一起成为 天体力学的创立者 。 欧拉研究了流体的运动性质,建立了理想流体运动的基 本微分方程 ,成为流体力学的 创始人。 欧拉把自己所建立的理想流体运动的基本方程用于人体血液的流动,从而在生物学上添上了他的贡献,又以流体力学、潮汐理论为基础,丰富和发展了船舶设计制造及航海理论。 1783年9月18日下午,欧拉一边和小孙女逗着玩,一边思考着计算天王星的轨迹,突然,他从椅子上滑下来,嘴里轻声说:“我死了”。一位科学巨匠就这样停止了生命。 欧拉从19岁开始写作,直到逝世,留下了浩如烟海的论文、著作,甚至在他死后,他留下的许多手稿还丰富了后47年的圣彼得堡科学院学报。就科研成果方面来说,欧拉是数学史上或者说是自然科学史上首屈一指的。 历史学家把欧拉和阿基米德、牛顿、高斯列为有史以来贡献最大的四位数学家,依据是他们都有一个共同点,就是在创建纯粹理论的同时,还应用这些数学工具去解决大量天文、物理和力学等方面的实际问题,他们的工作是跨学科的,他们不断地从实践中吸取丰富的营养,但又不满足于具体问题的解决,而是把宇宙看作是一个有机的整体,力图揭示它的奥秘和内在规律。 法国数学家拉普拉斯则认为:读读欧拉,他是所有人的老师。瑞士教育与研究国务秘书Charles Kleiber曾表示:“没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活。惊叹欧拉 丰功伟绩;钦佩
欧拉坚持不懈的治学 精神;学习欧拉 思想和方法.祝同学们在新的学期里
更高,更快,更强
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
