选修3-1 第六讲 近代数学两巨星分析的化身──欧拉课件20张PPT
文档属性
| 名称 | 选修3-1 第六讲 近代数学两巨星分析的化身──欧拉课件20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-14 00:00:00 | ||
图片预览








文档简介
课件20张PPT。伟大的数学家——欧拉
人物简介
欧拉生平
主要贡献
欧拉之名
纪念活动
人物简介莱昂哈德·欧拉(Leonhard Euler ,1707年4月5日~1783年9月18日)是瑞士数学家和物理学家。他被数学史学者称为历史上最伟大的两位数学家之一.
欧拉还是数学史上最多产的数学家,他一生写下886种书籍论文,平均每年写出800多页,彼得堡科学院为了整理他的著作,足足忙碌了47年。欧拉生平欧拉1707年4月15日出生於瑞士的巴塞尔,1783年9月18日於俄国的彼得堡去逝。
欧拉出生於牧师家庭,自幼受到父亲的教育。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。
1727年欧拉到俄国的彼得堡科学院从事研究工作,并在1731年接替丹尼尔第一伯努利,成为物理学教授。
欧拉在分析学、数论及力学方面均有出色的表现。此外,欧拉还应俄国政府的要求,解决了不少如地图学、造船业等的实际问题。
1735年,他因工作过度以致右眼失明。
1741年,他受到普鲁士腓特烈大帝的邀请到德国科学院担任物理数学所所长一职,长达25年。
他在柏林期间的研究内容更加广泛,涉及行星运动、刚体运动、热力学、弹道学、人口学等等,这些工作与他的数学研究互相推动着。
1766年,他应俄国沙皇喀德林二世的礼聘重回彼得堡
1771年,一场重病使他的左眼亦完全失明,但他以其惊人的记忆力和心算技巧继续从事科学创作。
1783年9月18日逝世于俄国的彼得堡.
欧拉的主要贡献1.数论
欧拉首先发现二次互反律,欧拉还引入了以他名字命名的数论中的欧拉函数
欧拉证明过一个定理,如今叫中国剩余定理,也叫孙子定理,在孙子算经中有一个简单的特例,后由南宋数学家秦九韶给出了一般形式。后来欧拉、高斯分别重新发现了这个定理,并给出了证明。
2.代数
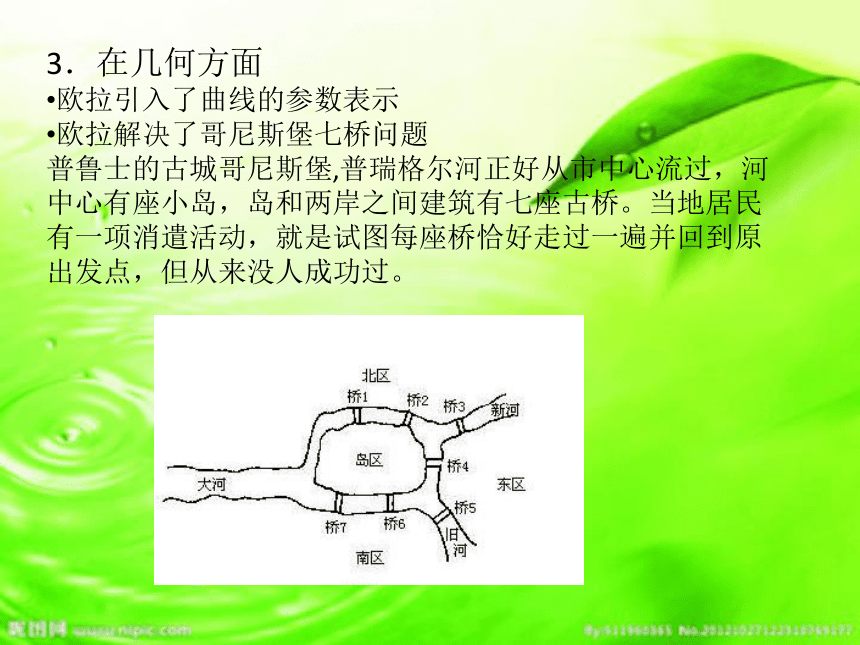
欧拉《代数学入门》一书,是16世纪中期开始发展的代数学的一个系统总结。3.在几何方面
欧拉引入了曲线的参数表示
欧拉解决了哥尼斯堡七桥问题
普鲁士的古城哥尼斯堡,普瑞格尔河正好从市中心流过,河中心有座小岛,岛和两岸之间建筑有七座古桥。当地居民有一项消遣活动,就是试图每座桥恰好走过一遍并回到原出发点,但从来没人成功过。 欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0 个就是2 个(连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两端,因此任何图能一笔画成,奇点要么没有要么在两端) 欧拉证明了这种走法是不可能的。他对七桥问题的抽象和论证思想,开创了一个新的学科:图论(Graph)。4.在微积分方面
先后发表了《无穷小分析引论》(1748)、《微分学》(1755)、《积分学》(1768)等著作。
欧拉提出了自己的函数概念:一个变量的函数是由该变量和一些数或常量以任何方式构成的解析表达式。
欧拉又再次扩张了他的函数概念:如果某些变量以这样一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随之变化,则将前面的变量称为后面变量的函数。(函数概念的雏形)此后经过众多数学家一百多年的发展和完善,才得到现在函数的概念。
把实函数的许多结果形式地推广到复数域,推动了复变函数理论的发展。
5.在初等数学方面
欧拉抛弃了陈旧的概念,采用新的思想方法去叙述、处理问题建立了新的初等数学体系。6.在变分学方面
研究出欧拉方程。1734年,他推广了最速降线问题。
1744年,欧拉的《寻求具有某种极大或极小性质的曲线的方法》一书出版。这是变分学史上的里程碑,它标志着变分法作为一个新的数学分析的诞生。
7.力学
欧拉将数学分析方法用于力学,在力学各个领域中都有突 出贡献;
他是刚体动力学和流体力学的奠基者,弹性系统销定性理论的开创人。 9.其他贡献
欧拉的一生,是为数学发展而奋斗的一生,他那杰出的智慧,顽强的毅力,孜孜不倦的奋斗精神和高尚的科学道德,永远是值得我们学习的.欧拉还创设了许多数学符号,例如π(1736年),i(1777年),e(1748年),sin和cos(1748年),tg(1753年),△x(1755年),Σ(1755年),f(x)(1734年)等.8.在微分方程方面
欧拉将一类二阶方程通过变量替换化为一阶方程给出了用累次积分计算这种积分的程序
研究了谐振子方程、谐振子的强迫振动方程,并得到了解答
指出弦的运动是周期性的,还用三角级数表出了解。
1.欧拉恒等式以欧拉的名字命名的重要常数,公式和定理(数学中最美公式)2.68127101555844666103.欧拉角
用来确定定点转动刚体位置的3个一组独立角参量,由章动角θ、旋进角(即进动角)ψ和自转角j组成,为欧拉首先提出而得名。
4.欧拉线
三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线,且外心到重心的距离等于垂心到重心距离的一半。 莱昂哈德·欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的重心在欧拉线上,即三角形的重心、垂心和外心共线。他证明了在任意三角形中,以上四点共线。欧拉线上的四点中,九点圆圆心到垂心和外心的距离相等,而且重心到外心的距离是重心到垂心距离的一半。
如右图,欧拉线(图中的红线)是指过三角形的垂心(蓝)、外心(绿)、重心(黄)和欧拉圆圆心(红点)的一条直线。5.欧拉方程
1755年,瑞士数学家L.欧拉在《流体运动的一般原理》一书中首先提出这个方程。 在研究一些物理问题,如热的传导、圆膜的震动、电磁波的传播等问题时,常常碰到如下形式的方程:(ax^2D^2+bxD+c)y=f(x), 其中a、b、c是常数,这是一个二阶变系数线性微分方程。它的系数具有一定的规律:二阶导数D^2y的系数是二次函数ax^2,一阶导数Dy的系数是一次函数bx,y的系数是常数。这样的方程称为欧拉方程 6.欧拉函数
欧拉函数,在数论,对正整数n,欧拉函数是少于或等于n的数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为Euler's totient fun_ction、φ函数、欧拉商数等。 例如φ(8)=4,因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。纪念活动
前苏联
俄罗斯的近代数学可以认为从欧拉开始的,欧拉在俄国生活了 30 多年,他积极将先进的科学知识传入长期闭塞落后的俄罗斯,创立了俄罗斯第一个数学学派——欧拉学派,亲手将一大批俄罗斯青年引进了辉煌的数学殿堂。苏联于1957年发行了印有欧拉头像的邮票。文字内容为:欧拉,伟大的数学家和学者,诞辰250周年瑞士
在一个小国家里诞生一位科学巨匠,这在世界史上并不多见。瑞士数学家欧拉便是其中最出色的一位,虽然他成年以后一直生活在两座遥远的异国城市:彼得堡和柏林,他的肖像画却出现在瑞士法郎上,与英镑上的牛顿一起成为至今仍流通欧洲的纸币上仅有的两位科学家。?瑞士于1957年发行一套邮票,以此纪念欧拉的250周年诞辰,又于2007年发行新的纪念邮票,纪念欧拉诞辰300周年。?
中国
为庆祝欧拉诞辰300周年,瑞士政府、中国科学院及中国教育部于2007年4月23日下午在北京的中国科学院文献情报中心共同举办纪念活动,回顾欧拉的生平、工作及对现代生活的影响。瑞士教育与研究国务秘书Charles Kleiber在开幕致词中说:“今天,我们在这里纪念近代历史上最伟大的学者之一。没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活。”思考:从数学家欧拉的身上学到了什么?谢谢!
欧拉生平
主要贡献
欧拉之名
纪念活动
人物简介莱昂哈德·欧拉(Leonhard Euler ,1707年4月5日~1783年9月18日)是瑞士数学家和物理学家。他被数学史学者称为历史上最伟大的两位数学家之一.
欧拉还是数学史上最多产的数学家,他一生写下886种书籍论文,平均每年写出800多页,彼得堡科学院为了整理他的著作,足足忙碌了47年。欧拉生平欧拉1707年4月15日出生於瑞士的巴塞尔,1783年9月18日於俄国的彼得堡去逝。
欧拉出生於牧师家庭,自幼受到父亲的教育。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。
1727年欧拉到俄国的彼得堡科学院从事研究工作,并在1731年接替丹尼尔第一伯努利,成为物理学教授。
欧拉在分析学、数论及力学方面均有出色的表现。此外,欧拉还应俄国政府的要求,解决了不少如地图学、造船业等的实际问题。
1735年,他因工作过度以致右眼失明。
1741年,他受到普鲁士腓特烈大帝的邀请到德国科学院担任物理数学所所长一职,长达25年。
他在柏林期间的研究内容更加广泛,涉及行星运动、刚体运动、热力学、弹道学、人口学等等,这些工作与他的数学研究互相推动着。
1766年,他应俄国沙皇喀德林二世的礼聘重回彼得堡
1771年,一场重病使他的左眼亦完全失明,但他以其惊人的记忆力和心算技巧继续从事科学创作。
1783年9月18日逝世于俄国的彼得堡.
欧拉的主要贡献1.数论
欧拉首先发现二次互反律,欧拉还引入了以他名字命名的数论中的欧拉函数
欧拉证明过一个定理,如今叫中国剩余定理,也叫孙子定理,在孙子算经中有一个简单的特例,后由南宋数学家秦九韶给出了一般形式。后来欧拉、高斯分别重新发现了这个定理,并给出了证明。
2.代数
欧拉《代数学入门》一书,是16世纪中期开始发展的代数学的一个系统总结。3.在几何方面
欧拉引入了曲线的参数表示
欧拉解决了哥尼斯堡七桥问题
普鲁士的古城哥尼斯堡,普瑞格尔河正好从市中心流过,河中心有座小岛,岛和两岸之间建筑有七座古桥。当地居民有一项消遣活动,就是试图每座桥恰好走过一遍并回到原出发点,但从来没人成功过。 欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0 个就是2 个(连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两端,因此任何图能一笔画成,奇点要么没有要么在两端) 欧拉证明了这种走法是不可能的。他对七桥问题的抽象和论证思想,开创了一个新的学科:图论(Graph)。4.在微积分方面
先后发表了《无穷小分析引论》(1748)、《微分学》(1755)、《积分学》(1768)等著作。
欧拉提出了自己的函数概念:一个变量的函数是由该变量和一些数或常量以任何方式构成的解析表达式。
欧拉又再次扩张了他的函数概念:如果某些变量以这样一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随之变化,则将前面的变量称为后面变量的函数。(函数概念的雏形)此后经过众多数学家一百多年的发展和完善,才得到现在函数的概念。
把实函数的许多结果形式地推广到复数域,推动了复变函数理论的发展。
5.在初等数学方面
欧拉抛弃了陈旧的概念,采用新的思想方法去叙述、处理问题建立了新的初等数学体系。6.在变分学方面
研究出欧拉方程。1734年,他推广了最速降线问题。
1744年,欧拉的《寻求具有某种极大或极小性质的曲线的方法》一书出版。这是变分学史上的里程碑,它标志着变分法作为一个新的数学分析的诞生。
7.力学
欧拉将数学分析方法用于力学,在力学各个领域中都有突 出贡献;
他是刚体动力学和流体力学的奠基者,弹性系统销定性理论的开创人。 9.其他贡献
欧拉的一生,是为数学发展而奋斗的一生,他那杰出的智慧,顽强的毅力,孜孜不倦的奋斗精神和高尚的科学道德,永远是值得我们学习的.欧拉还创设了许多数学符号,例如π(1736年),i(1777年),e(1748年),sin和cos(1748年),tg(1753年),△x(1755年),Σ(1755年),f(x)(1734年)等.8.在微分方程方面
欧拉将一类二阶方程通过变量替换化为一阶方程给出了用累次积分计算这种积分的程序
研究了谐振子方程、谐振子的强迫振动方程,并得到了解答
指出弦的运动是周期性的,还用三角级数表出了解。
1.欧拉恒等式以欧拉的名字命名的重要常数,公式和定理(数学中最美公式)2.68127101555844666103.欧拉角
用来确定定点转动刚体位置的3个一组独立角参量,由章动角θ、旋进角(即进动角)ψ和自转角j组成,为欧拉首先提出而得名。
4.欧拉线
三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线,且外心到重心的距离等于垂心到重心距离的一半。 莱昂哈德·欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的重心在欧拉线上,即三角形的重心、垂心和外心共线。他证明了在任意三角形中,以上四点共线。欧拉线上的四点中,九点圆圆心到垂心和外心的距离相等,而且重心到外心的距离是重心到垂心距离的一半。
如右图,欧拉线(图中的红线)是指过三角形的垂心(蓝)、外心(绿)、重心(黄)和欧拉圆圆心(红点)的一条直线。5.欧拉方程
1755年,瑞士数学家L.欧拉在《流体运动的一般原理》一书中首先提出这个方程。 在研究一些物理问题,如热的传导、圆膜的震动、电磁波的传播等问题时,常常碰到如下形式的方程:(ax^2D^2+bxD+c)y=f(x), 其中a、b、c是常数,这是一个二阶变系数线性微分方程。它的系数具有一定的规律:二阶导数D^2y的系数是二次函数ax^2,一阶导数Dy的系数是一次函数bx,y的系数是常数。这样的方程称为欧拉方程 6.欧拉函数
欧拉函数,在数论,对正整数n,欧拉函数是少于或等于n的数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为Euler's totient fun_ction、φ函数、欧拉商数等。 例如φ(8)=4,因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。纪念活动
前苏联
俄罗斯的近代数学可以认为从欧拉开始的,欧拉在俄国生活了 30 多年,他积极将先进的科学知识传入长期闭塞落后的俄罗斯,创立了俄罗斯第一个数学学派——欧拉学派,亲手将一大批俄罗斯青年引进了辉煌的数学殿堂。苏联于1957年发行了印有欧拉头像的邮票。文字内容为:欧拉,伟大的数学家和学者,诞辰250周年瑞士
在一个小国家里诞生一位科学巨匠,这在世界史上并不多见。瑞士数学家欧拉便是其中最出色的一位,虽然他成年以后一直生活在两座遥远的异国城市:彼得堡和柏林,他的肖像画却出现在瑞士法郎上,与英镑上的牛顿一起成为至今仍流通欧洲的纸币上仅有的两位科学家。?瑞士于1957年发行一套邮票,以此纪念欧拉的250周年诞辰,又于2007年发行新的纪念邮票,纪念欧拉诞辰300周年。?
中国
为庆祝欧拉诞辰300周年,瑞士政府、中国科学院及中国教育部于2007年4月23日下午在北京的中国科学院文献情报中心共同举办纪念活动,回顾欧拉的生平、工作及对现代生活的影响。瑞士教育与研究国务秘书Charles Kleiber在开幕致词中说:“今天,我们在这里纪念近代历史上最伟大的学者之一。没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活。”思考:从数学家欧拉的身上学到了什么?谢谢!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
