人教版必修一集合小结课件(25张)
文档属性
| 名称 | 人教版必修一集合小结课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 335.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 00:00:00 | ||
图片预览

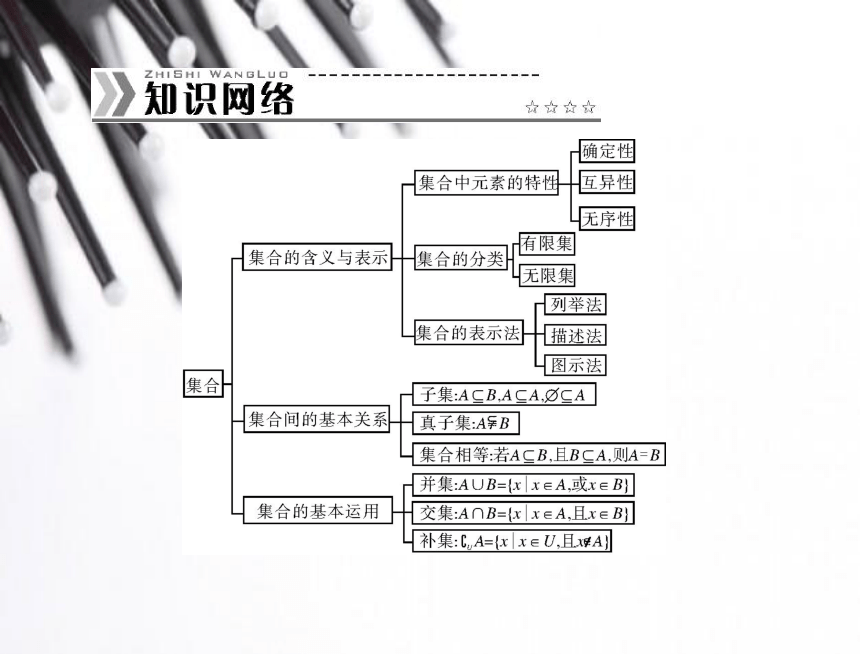
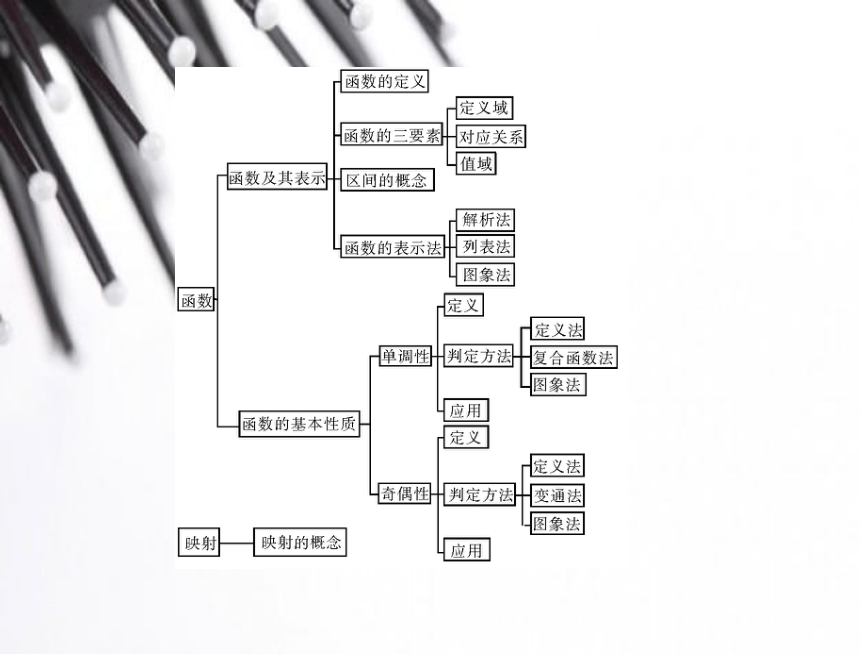




文档简介
课件25张PPT。集合小结专题一数形结合思想在函数中的应用 数形结合思想是数学中重要的思想方法之一,具有直观性、
灵活性和深刻性的特点,并跨越各学科界限,有较强的综合性,
加强这方面的学习和训练,对巩固数学知识、打好基础、提高
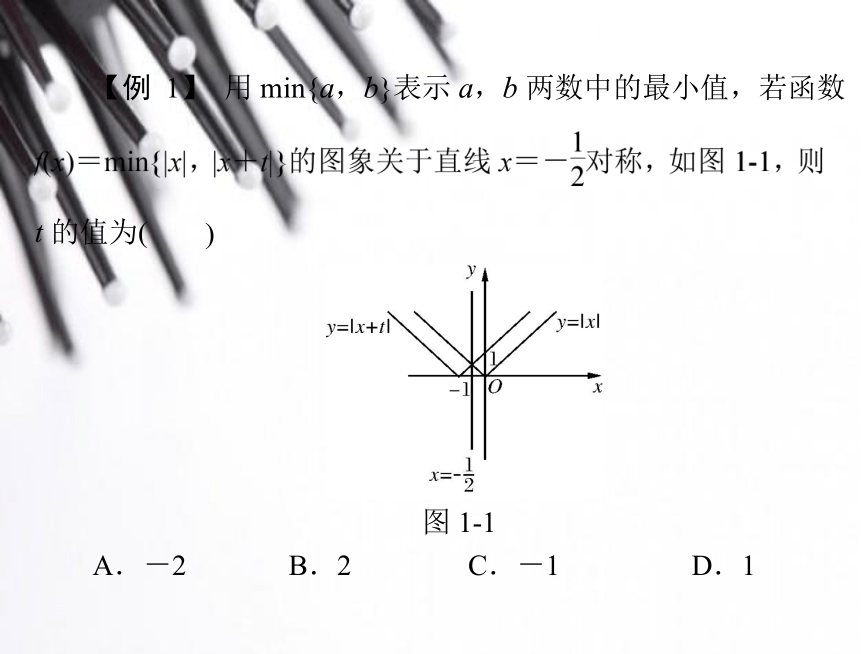
能力有重要作用.【例 1】 用 min{a,b}表示 a,b 两数中的最小值,若函数t 的值为()图 1-1A.-2B.2C.-1D.1思维突破:由图形可以看出,要使图象关于x=- 对称,则 t=1.答案:D 数形结合的实质是“以形助数”或“以数解
形”,运用数形结合思想解题,不仅直观且易于寻找解题途径,
更可以避免繁杂的计算和推理. 【互动与探究】
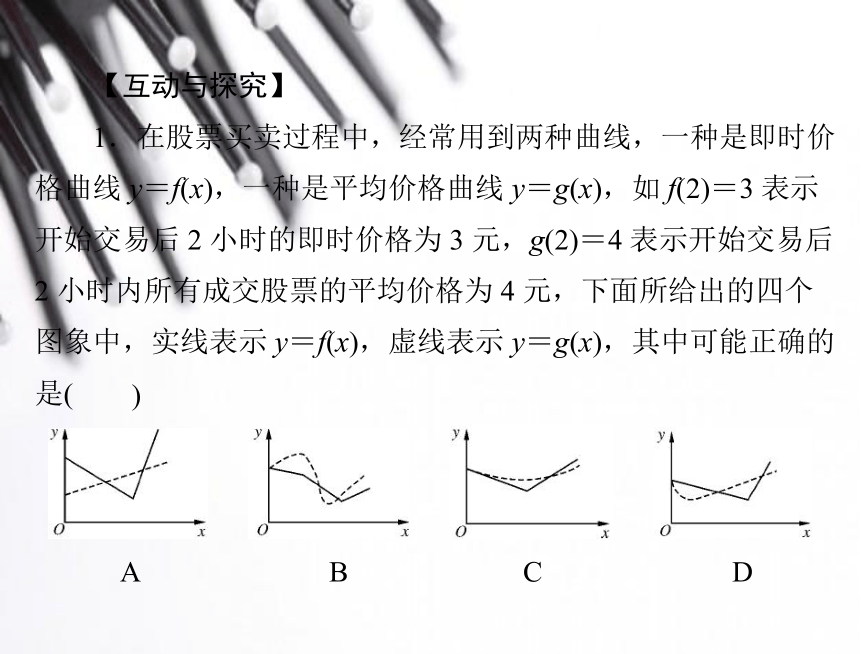
1.在股票买卖过程中,经常用到两种曲线,一种是即时价
格曲线 y=f(x),一种是平均价格曲线 y=g(x),如 f(2)=3 表示
开始交易后 2 小时的即时价格为 3 元,g(2)=4 表示开始交易后
2 小时内所有成交股票的平均价格为 4 元,下面所给出的四个
图象中,实线表示 y=f(x),虚线表示 y=g(x),其中可能正确的是()ABCD解析:f(0)与 g(0)应该相等,故排除 A,B 中开始交易的平均价格高于即时价格,D 中恰好相反.故选 C.答案:C 2.已知甲、乙两车由同一起点同时出发,并沿同一路线(假
定为直线)行驶.甲车和乙车的速度曲线分别为 v 甲和 v 乙(如图
1-2).那么对于图中给定的 t0 和 t1,下列判断中一定正确的是( )
A.在 t1 时刻,甲车在乙车的前面
B.t1 时刻后,甲车在乙车的后面
C.在 t0 时刻,两车的位置相同D.t0 时刻后,乙车在甲车的前面图 1-2 解析:由图象可知:曲线 v甲比 v乙在 0~t0,0~t1 与x 轴所
围成图形面积大,则在t0 和t1 时刻,甲车均在乙车前面.故选A.
答案:A专题二分类讨论思想在函数中的应用 解分类讨论问题时,以下几点要予以足够重视:
(1)做到分类讨论不重复、不遗漏.
(2)克服分类讨论中的主观性和盲目性.
(3)注意掌握好基础知识、基本方法,这是解分类讨论问题
的前提条件. 【例 2】 已知二次函数 f(x)=x2-16x+q+3.
(1)若函数在区间[-1,1]上存在零点,求实数 q 的取值范围;
(2)是否存在常数 t(t≥0),当 x∈[t,10]时,f(x)的值域为区间
D,且区间 D 的长度为 12-t(视区间[a,b]的长度为 b-a).
解:(1)∵f(x)=x2-16x+q+3 的对称轴是 x=8,
∴f(x)在区间[-1,1]上是减函数.
函数在区间[-1,1]上存在零点,则必有:f(1)≤0,
f(-1)≥0,即1-16+q+3≤0,
1+16+q+3≥0,∴-20≤q≤12. (2)当 0≤t<10 时,f(x)在区间[0,8]上是减函数,在区间(8,10]
上是增函数,且对称轴是 x=8.
①当 0≤t≤6 时,在区间[t,10]上,f(t)最大,f(8)最小,
∴f(t)-f(8)=12-t,即 t2-15t+52=0.②当 6∴f(10)-f(8)=12-t,解得 t=8.
∴f(10)-f(t)=12-t,即 t2-17t+72=0.
解得 t=8 或 t=9,∴t=9. “区间固定对称轴动”以及“对称轴固定区
间动”是二次函数中分类讨论的最基本的两种题型.本例中的
二次函数是对称轴固定,而区间不固定,因此需要讨论该区间
相对于对称轴的位置关系,即分情况讨论.③当 8∵对任意 x∈(-∞,0)∪(0,+∞),
f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数.取 x=±1,得 f(-1)+f(1)=2≠0,f(-1)-f(1)=-2a≠0,
∴f(-1)≠-f(1),f(-1)≠f(1).
∴函数 f(x)既不是奇函数,也不是偶函数.(2)设 2≤x1<x2, 要使函数 f(x) 在 x ∈[2 ,+∞) 上为增函数,必须 f(x1) -
f(x2)<0 恒成立.
∵x1-x2<0,∴a<x1x2(x1+x2)恒成立.
又∵x1+x2>4,x1x2>4,
∴x1x2(x1+x2)>16.
∴a 的取值范围是(-∞,16].专题三函数的实际应用 【例 3】 我国是水资源比较贫乏的国家之一,各地采用价
格调控等手段以达到节约用水的目的,某市用水收费标准是:
水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量 m 立方米时,只付基本费
9 元和每户每月定额损耗费 a 元;
②若每月用水量超过 m 立方米时,除了付基本费和定额损
耗费外,超过部分每立方米付 n 元的超额费;
③每户每月的定额损耗费 a 不超过 5 元.(1)求每户每月水费 y(单位:元)与用水量 x(单位:立方米)的函数关系式;(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:试分析该家庭今年一、二、三各月份的用水量是否超过最低限量 ,并求 m,n,a 的值.解:(1)依题意,得 (2)∵0≤a≤5,∴9<9+a≤14.
由于该家庭今年一、二月份的水费均大于 14 元,故用水量
4 立方米,5 立方米都大于最低限量 m 立方米.两式相减,得 n=6.
代入 17=9+n(4-m)+a,得 a=6m-16.
又三月份用水量为 2.5 立方米,得 a=6m-13,
这与 a=6m-16 矛盾. ∴m≥2.5,即该家庭三月份用水量 2.5 平方米没有超最低
限量.【互动与探究】 4.某学校要建造一个面积为 10 000 平方米的运动场.如
图 1-3,运动场是由一个矩形 ABCD 和分别以 AD,BC 为直径
的两个半圆组成.跑道是一条宽 8 米的塑胶跑道,运动场除跑
道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为 150
元,草皮每平方米造价为 30 元.(1)设半圆的半径 OA=r(单位:米),试建立塑胶跑道面积 S与 r 的函数关系 S(r); (2)由于条件限制 r∈[30,40],问当 r 取何值时,运动场的造
价最低(精确到整数)?
图 1-3
解:(1)塑胶跑道面积为(2)设运动场的造价为 y 元,∴当 r∈[30,40]时,函数 y 单调递减.
上为减函数.
∴当 r=40 时,ymin≈636 461.
即运动场的造价最低为636 461元.
灵活性和深刻性的特点,并跨越各学科界限,有较强的综合性,
加强这方面的学习和训练,对巩固数学知识、打好基础、提高
能力有重要作用.【例 1】 用 min{a,b}表示 a,b 两数中的最小值,若函数t 的值为()图 1-1A.-2B.2C.-1D.1思维突破:由图形可以看出,要使图象关于x=- 对称,则 t=1.答案:D 数形结合的实质是“以形助数”或“以数解
形”,运用数形结合思想解题,不仅直观且易于寻找解题途径,
更可以避免繁杂的计算和推理. 【互动与探究】
1.在股票买卖过程中,经常用到两种曲线,一种是即时价
格曲线 y=f(x),一种是平均价格曲线 y=g(x),如 f(2)=3 表示
开始交易后 2 小时的即时价格为 3 元,g(2)=4 表示开始交易后
2 小时内所有成交股票的平均价格为 4 元,下面所给出的四个
图象中,实线表示 y=f(x),虚线表示 y=g(x),其中可能正确的是()ABCD解析:f(0)与 g(0)应该相等,故排除 A,B 中开始交易的平均价格高于即时价格,D 中恰好相反.故选 C.答案:C 2.已知甲、乙两车由同一起点同时出发,并沿同一路线(假
定为直线)行驶.甲车和乙车的速度曲线分别为 v 甲和 v 乙(如图
1-2).那么对于图中给定的 t0 和 t1,下列判断中一定正确的是( )
A.在 t1 时刻,甲车在乙车的前面
B.t1 时刻后,甲车在乙车的后面
C.在 t0 时刻,两车的位置相同D.t0 时刻后,乙车在甲车的前面图 1-2 解析:由图象可知:曲线 v甲比 v乙在 0~t0,0~t1 与x 轴所
围成图形面积大,则在t0 和t1 时刻,甲车均在乙车前面.故选A.
答案:A专题二分类讨论思想在函数中的应用 解分类讨论问题时,以下几点要予以足够重视:
(1)做到分类讨论不重复、不遗漏.
(2)克服分类讨论中的主观性和盲目性.
(3)注意掌握好基础知识、基本方法,这是解分类讨论问题
的前提条件. 【例 2】 已知二次函数 f(x)=x2-16x+q+3.
(1)若函数在区间[-1,1]上存在零点,求实数 q 的取值范围;
(2)是否存在常数 t(t≥0),当 x∈[t,10]时,f(x)的值域为区间
D,且区间 D 的长度为 12-t(视区间[a,b]的长度为 b-a).
解:(1)∵f(x)=x2-16x+q+3 的对称轴是 x=8,
∴f(x)在区间[-1,1]上是减函数.
函数在区间[-1,1]上存在零点,则必有:f(1)≤0,
f(-1)≥0,即1-16+q+3≤0,
1+16+q+3≥0,∴-20≤q≤12. (2)当 0≤t<10 时,f(x)在区间[0,8]上是减函数,在区间(8,10]
上是增函数,且对称轴是 x=8.
①当 0≤t≤6 时,在区间[t,10]上,f(t)最大,f(8)最小,
∴f(t)-f(8)=12-t,即 t2-15t+52=0.②当 6
∴f(10)-f(t)=12-t,即 t2-17t+72=0.
解得 t=8 或 t=9,∴t=9. “区间固定对称轴动”以及“对称轴固定区
间动”是二次函数中分类讨论的最基本的两种题型.本例中的
二次函数是对称轴固定,而区间不固定,因此需要讨论该区间
相对于对称轴的位置关系,即分情况讨论.③当 8
f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数.取 x=±1,得 f(-1)+f(1)=2≠0,f(-1)-f(1)=-2a≠0,
∴f(-1)≠-f(1),f(-1)≠f(1).
∴函数 f(x)既不是奇函数,也不是偶函数.(2)设 2≤x1<x2, 要使函数 f(x) 在 x ∈[2 ,+∞) 上为增函数,必须 f(x1) -
f(x2)<0 恒成立.
∵x1-x2<0,∴a<x1x2(x1+x2)恒成立.
又∵x1+x2>4,x1x2>4,
∴x1x2(x1+x2)>16.
∴a 的取值范围是(-∞,16].专题三函数的实际应用 【例 3】 我国是水资源比较贫乏的国家之一,各地采用价
格调控等手段以达到节约用水的目的,某市用水收费标准是:
水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量 m 立方米时,只付基本费
9 元和每户每月定额损耗费 a 元;
②若每月用水量超过 m 立方米时,除了付基本费和定额损
耗费外,超过部分每立方米付 n 元的超额费;
③每户每月的定额损耗费 a 不超过 5 元.(1)求每户每月水费 y(单位:元)与用水量 x(单位:立方米)的函数关系式;(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:试分析该家庭今年一、二、三各月份的用水量是否超过最低限量 ,并求 m,n,a 的值.解:(1)依题意,得 (2)∵0≤a≤5,∴9<9+a≤14.
由于该家庭今年一、二月份的水费均大于 14 元,故用水量
4 立方米,5 立方米都大于最低限量 m 立方米.两式相减,得 n=6.
代入 17=9+n(4-m)+a,得 a=6m-16.
又三月份用水量为 2.5 立方米,得 a=6m-13,
这与 a=6m-16 矛盾. ∴m≥2.5,即该家庭三月份用水量 2.5 平方米没有超最低
限量.【互动与探究】 4.某学校要建造一个面积为 10 000 平方米的运动场.如
图 1-3,运动场是由一个矩形 ABCD 和分别以 AD,BC 为直径
的两个半圆组成.跑道是一条宽 8 米的塑胶跑道,运动场除跑
道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为 150
元,草皮每平方米造价为 30 元.(1)设半圆的半径 OA=r(单位:米),试建立塑胶跑道面积 S与 r 的函数关系 S(r); (2)由于条件限制 r∈[30,40],问当 r 取何值时,运动场的造
价最低(精确到整数)?
图 1-3
解:(1)塑胶跑道面积为(2)设运动场的造价为 y 元,∴当 r∈[30,40]时,函数 y 单调递减.
上为减函数.
∴当 r=40 时,ymin≈636 461.
即运动场的造价最低为636 461元.
