人教版必修一2.3信息技术应用用计算机绘制幂函数模型课件(15张)
文档属性
| 名称 | 人教版必修一2.3信息技术应用用计算机绘制幂函数模型课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 279.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 21:02:08 | ||
图片预览





文档简介
课件15张PPT。1.3信息技术应用用计算机绘制幂函数模型教学课件
一、课堂准备1、运行环境:几何画板4.0以上版本
2、模型主要功能:配合教科书“2.3 幂函数”和”3.2函数模型及其应用”的教学。利用几何画板绘制函数图象的功能,绘制出幂函数的图象,再利用幂函数的图象研究函数的性质或增长规律。
二、模型制作过程(1)新建画板窗口。单击【Graph】(图表)菜单中的【Define Coordinate System】(建立直角坐标系),建立直角坐标系。选中原点,按Ctrl+K,给原点加注标签A,并用【文本】工具把标签改为O。
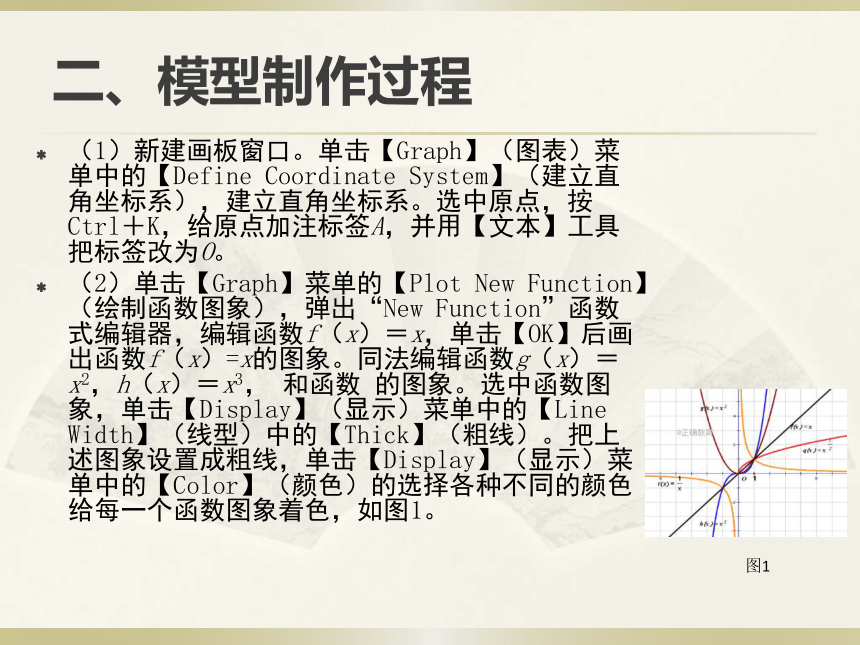
(2)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,编辑函数f(x)=x,单击【OK】后画出函数f(x)=x的图象。同法编辑函数g(x)=x2,h(x)=x3, 和函数 的图象。选中函数图象,单击【Display】(显示)菜单中的【Line Width】(线型)中的【Thick】(粗线)。把上述图象设置成粗线,单击【Display】(显示)菜单中的【Color】(颜色)的选择各种不同的颜色给每一个函数图象着色,如图1。
图1(3)再选中直线f(x)=x,单击【Edit】(编辑)菜单,选择【Action Buttons】(操作类按钮),单击【Hide/Show】(隐藏/显示),此时屏幕上出现【Hide Function Plot】(隐藏对象)按钮,选择【文本工具】,双击【Hide Function Plot】按钮,出现对话框,将其中的【Label】(标签)改为“f(x)=x”,再单击【确定】。此时,单击“f(x)=x”按钮就会隐藏或显示直线f(x)=x。用同样的方法制作【Hide Function Plot】按钮g(x)=x2, , 和 ,如图2。
如图2(4)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,将【Page Name】(页面名称)改为“画图象”,单击【OK】。
(5)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,
单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“g(x)=x2”。
(6)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,2,单击【OK】后画出函数g(x)=x2的图象。选中函数g(x)=x2的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(7)双击y轴,即将y轴标记为镜面,选中点A,单击【Transform】(变换)菜单的【Reflect】(反射),屏幕上出现点A关于y轴的对称点,发现该点也落在曲线g(x)=x2上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
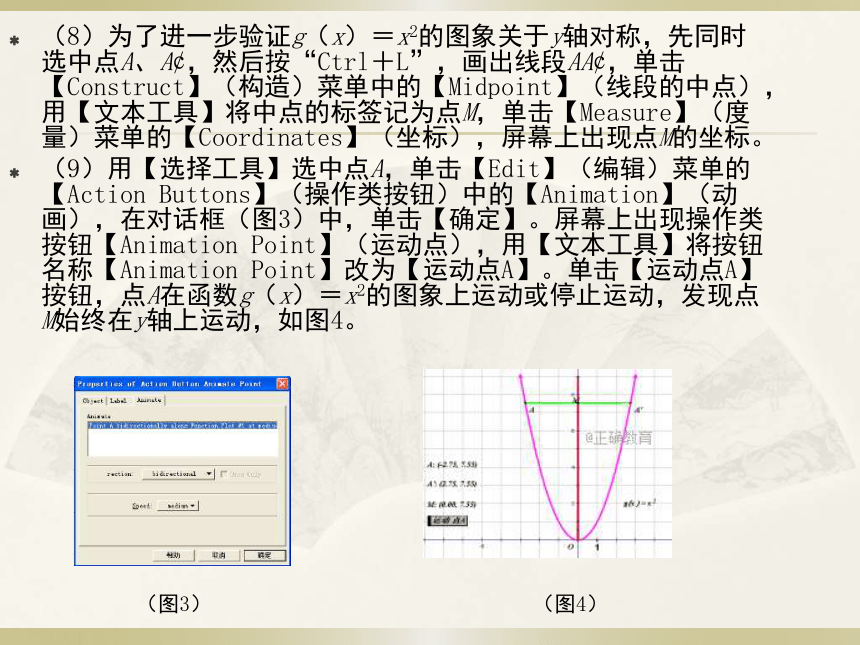
(8)为了进一步验证g(x)=x2的图象关于y轴对称,先同时选中点A、A¢,然后按“Ctrl+L”,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),用【文本工具】将中点的标签记为点M,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点M的坐标。
(9)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(图3)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数g(x)=x2的图象上运动或停止运动,发现点M始终在y轴上运动,如图4。
(图3)(图4)(10)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(11)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,3,单击【OK】后画出函数 的图象。选中函数 的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(12)双击原点O,即将原点O标记为对称中心,选中点A,单击【Transform】(变换)菜单的【Rotate】(旋转),屏幕上出现对话框(图5),将图5中的“90。0”改为“180。0”,再单击【Rotate】,此时,屏幕上出现点A关于原点O的对称点,发现该点也落在曲线 上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
(13)为了进一步验证 的图象关于原点O中心对称,先同时选中点A、A¢,然后按Ctrl+L,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现线段AA¢中点的坐标O(0,0)。
(14)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(如图5所示)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数 的图象上运动或停止运动,发现线段AA¢中点始终与原点O重合,如图6。
(如图5)(如图6)(15)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(16)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,-1,单击【OK】后画出函数 的图象。选中函数 的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(17)双击原点O,即将原点O标记为对称中心,选中点A,单击【Transform】(变换)菜单的【Rotate】(旋转),屏幕上出现对话框(图5),将图5中的“90。0”改为“180。0”,再单击【Rotate】,此时,屏幕上出现点A关于原点O的对称点,发现该点也落在曲线 上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
(18)为了进一步验证 的图象关于原点O中心对称,先同时选中点A、A¢,然后按“Ctrl+L”,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),屏幕上出现线段AA¢中点的为原点O。
(19)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(如图3所示)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数 的图象上运动或停止运动,发现线段AA¢中点始终与原点O重合,如图7。
(如图7)(20)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(21)单击【Graph】菜单的【New Parameter】(新建参数),出现对话框(图8),将图8中的【Name】(名称)“t[1]”改为“p”,【Value】(值)“1。0”改为“7。0”,再单击【OK】。屏幕上出现“p=1。00”,同法再新建参数“q=1。00”。 (图8)(22)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,(,p,/,q,),除p、q在屏幕上单击外,其余的都在函数编辑器上,单击【OK】后屏幕上出现函数 的图象,如图9。
(图9)三、制作模型使用说明: 1。在页面“画图象”中单击“f(x)=x”,“g(x)=x2”,“ ”,“ ”,和“ ”按纽就会隐藏或显示相应函数的图象。
2。在页面“g(x)=x2”,“ ”和“ ”中,单击按纽【运动点A】,点A就会在相应的函数图象上运动或停止运动,同时点A与点A/ 的坐标也跟着发生变化,可以让学生观察点A与点A¢的坐标的关系,也可以让学生观察线段AA¢中点的位置特征,通过观察上述函数的图象特征来探究函数的性质(定义域、值域、奇偶性、单调性等)。
3。在页面“ ”中,选中函数 的图象,单击【Display】(显示)菜单中的【Trace Function Plot 】(追踪函数图象)。任意选中“p=1。00”或“q=1。00”,按“+”或“-”号改变p、q的值,同时屏幕上会出现各种幂函数的图象,使学生对幂函数的图象与性质有比较全面的认识。
四、根据制作的幂函数模型分析 1、幂函数相关性质如何从图像上体现出来?增长规律如何?
2、对于本案例,请同学们利用几何画板信息技术探索有误其他函数模型,并讨论哪种函数模型最符合实际,谈谈你的理解?六、小结 1、模型制作准备
2、操作步骤
3、模型使用和分析
2、模型主要功能:配合教科书“2.3 幂函数”和”3.2函数模型及其应用”的教学。利用几何画板绘制函数图象的功能,绘制出幂函数的图象,再利用幂函数的图象研究函数的性质或增长规律。
二、模型制作过程(1)新建画板窗口。单击【Graph】(图表)菜单中的【Define Coordinate System】(建立直角坐标系),建立直角坐标系。选中原点,按Ctrl+K,给原点加注标签A,并用【文本】工具把标签改为O。
(2)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,编辑函数f(x)=x,单击【OK】后画出函数f(x)=x的图象。同法编辑函数g(x)=x2,h(x)=x3, 和函数 的图象。选中函数图象,单击【Display】(显示)菜单中的【Line Width】(线型)中的【Thick】(粗线)。把上述图象设置成粗线,单击【Display】(显示)菜单中的【Color】(颜色)的选择各种不同的颜色给每一个函数图象着色,如图1。
图1(3)再选中直线f(x)=x,单击【Edit】(编辑)菜单,选择【Action Buttons】(操作类按钮),单击【Hide/Show】(隐藏/显示),此时屏幕上出现【Hide Function Plot】(隐藏对象)按钮,选择【文本工具】,双击【Hide Function Plot】按钮,出现对话框,将其中的【Label】(标签)改为“f(x)=x”,再单击【确定】。此时,单击“f(x)=x”按钮就会隐藏或显示直线f(x)=x。用同样的方法制作【Hide Function Plot】按钮g(x)=x2, , 和 ,如图2。
如图2(4)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,将【Page Name】(页面名称)改为“画图象”,单击【OK】。
(5)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,
单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“g(x)=x2”。
(6)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,2,单击【OK】后画出函数g(x)=x2的图象。选中函数g(x)=x2的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(7)双击y轴,即将y轴标记为镜面,选中点A,单击【Transform】(变换)菜单的【Reflect】(反射),屏幕上出现点A关于y轴的对称点,发现该点也落在曲线g(x)=x2上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
(8)为了进一步验证g(x)=x2的图象关于y轴对称,先同时选中点A、A¢,然后按“Ctrl+L”,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),用【文本工具】将中点的标签记为点M,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点M的坐标。
(9)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(图3)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数g(x)=x2的图象上运动或停止运动,发现点M始终在y轴上运动,如图4。
(图3)(图4)(10)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(11)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,3,单击【OK】后画出函数 的图象。选中函数 的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(12)双击原点O,即将原点O标记为对称中心,选中点A,单击【Transform】(变换)菜单的【Rotate】(旋转),屏幕上出现对话框(图5),将图5中的“90。0”改为“180。0”,再单击【Rotate】,此时,屏幕上出现点A关于原点O的对称点,发现该点也落在曲线 上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
(13)为了进一步验证 的图象关于原点O中心对称,先同时选中点A、A¢,然后按Ctrl+L,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现线段AA¢中点的坐标O(0,0)。
(14)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(如图5所示)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数 的图象上运动或停止运动,发现线段AA¢中点始终与原点O重合,如图6。
(如图5)(如图6)(15)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(16)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,-1,单击【OK】后画出函数 的图象。选中函数 的图象,单击【Construct】(构造)菜单的【Point On Function Plot】(对象上的点),用【文本工具】给点标签为A,再用【选择工具】选中点A,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A的坐标。
(17)双击原点O,即将原点O标记为对称中心,选中点A,单击【Transform】(变换)菜单的【Rotate】(旋转),屏幕上出现对话框(图5),将图5中的“90。0”改为“180。0”,再单击【Rotate】,此时,屏幕上出现点A关于原点O的对称点,发现该点也落在曲线 上。选择【文本工具】,将此点的标签记为“A¢”,再用【选择工具】选中点A¢,单击【Measure】(度量)菜单的【Coordinates】(坐标),屏幕上出现点A¢的坐标。
(18)为了进一步验证 的图象关于原点O中心对称,先同时选中点A、A¢,然后按“Ctrl+L”,画出线段AA¢,单击【Construct】(构造)菜单中的【Midpoint】(线段的中点),屏幕上出现线段AA¢中点的为原点O。
(19)用【选择工具】选中点A,单击【Edit】(编辑)菜单的【Action Buttons】(操作类按钮)中的【Animation】(动画),在对话框(如图3所示)中,单击【确定】。屏幕上出现操作类按钮【Animation Point】(运动点),用【文本工具】将按钮名称【Animation Point】改为【运动点A】。单击【运动点A】按钮,点A在函数 的图象上运动或停止运动,发现线段AA¢中点始终与原点O重合,如图7。
(如图7)(20)单击【File】(文件)菜单的【Document Options】(文档选项)对话框,单击【Add Page】(增加页),单击【Blank Page】(空白页),将页面名称改为“ ”。
(21)单击【Graph】菜单的【New Parameter】(新建参数),出现对话框(图8),将图8中的【Name】(名称)“t[1]”改为“p”,【Value】(值)“1。0”改为“7。0”,再单击【OK】。屏幕上出现“p=1。00”,同法再新建参数“q=1。00”。 (图8)(22)单击【Graph】菜单的【Plot New Function】(绘制函数图象),弹出“New Function”函数式编辑器,在对话框内依次单击x,^,(,p,/,q,),除p、q在屏幕上单击外,其余的都在函数编辑器上,单击【OK】后屏幕上出现函数 的图象,如图9。
(图9)三、制作模型使用说明: 1。在页面“画图象”中单击“f(x)=x”,“g(x)=x2”,“ ”,“ ”,和“ ”按纽就会隐藏或显示相应函数的图象。
2。在页面“g(x)=x2”,“ ”和“ ”中,单击按纽【运动点A】,点A就会在相应的函数图象上运动或停止运动,同时点A与点A/ 的坐标也跟着发生变化,可以让学生观察点A与点A¢的坐标的关系,也可以让学生观察线段AA¢中点的位置特征,通过观察上述函数的图象特征来探究函数的性质(定义域、值域、奇偶性、单调性等)。
3。在页面“ ”中,选中函数 的图象,单击【Display】(显示)菜单中的【Trace Function Plot 】(追踪函数图象)。任意选中“p=1。00”或“q=1。00”,按“+”或“-”号改变p、q的值,同时屏幕上会出现各种幂函数的图象,使学生对幂函数的图象与性质有比较全面的认识。
四、根据制作的幂函数模型分析 1、幂函数相关性质如何从图像上体现出来?增长规律如何?
2、对于本案例,请同学们利用几何画板信息技术探索有误其他函数模型,并讨论哪种函数模型最符合实际,谈谈你的理解?六、小结 1、模型制作准备
2、操作步骤
3、模型使用和分析
