1.5.1-曲边梯形的面积与定积分课件22张PPT
文档属性
| 名称 | 1.5.1-曲边梯形的面积与定积分课件22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:13:13 | ||
图片预览








文档简介
课件22张PPT。成都七中嘉祥外国语学校“聚焦课堂,提质增效”
高中数学教研组赛课
“团结协作 拼搏创新”——高中数学教研组团队赛课流程团队上课代表张依老师上课团队说课代表李志斌老师说课团队评课代表钟高介老师评课“聚焦课堂,提质增效”专家点评张依上课
《曲边梯形的面积与定积分》高中数学教研组 张 依
高一数学组 大学先修课
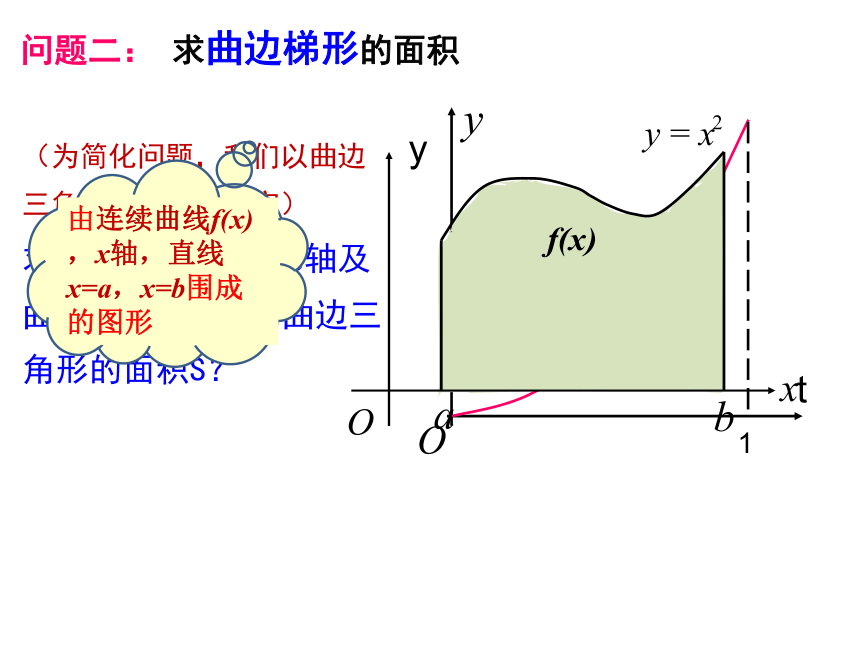
—曲边梯形面积与定积分 微积分基本定理2019-12-301例1 根据v-t图象,回答以下问题: 一.情景引入Q:物体运动中,4s内的位移问题一: 我们生活与工程实际中经常接触的物体变速运动v-t图象大都是曲线,此时位移面积怎么计算呢? 二.提出问题问题二: 求曲边梯形的面积(为简化问题,我们以曲边三角形为例进行研究)
求直线x?0、x?1、x轴及曲线y?x2所围成的曲边三角形的面积S?三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积三.小组合作---计算曲边梯形面积Q1: 结合“割圆术”,思考如何估算曲边三角形的面积?S1以直代曲方案1方案2方案311Q2: 以下分隔代替方式中,你会选择哪个方案来进行计算?均分将大曲边三角形等分为 n 个小曲边梯形 ,并将每个小曲边梯形面积用小矩形代替: 每个小矩形的宽:每个小矩形的面积:1.估算方案均匀分割+以直代曲三.小组合作---计算矩形面积和活动说明:
1.每3个组计算一种分割情况——矩形分割个数分别分5,10,20
2.学案已做好分隔,利用表格进行数据的整理,并使用公式和计算器计算,最终面积和结果精确到小数点后4位,计算完后,成员相互分享一下答案,确定最终发表结果。
3.计算时注意所给区间是[0,1]。
Q3: 当分割越细,即份数n无限增大时,矩形面积和与曲边三角形面积S有什么关系?当份数n无限增大时,矩形面积和无限逼近曲边三角形面积SS趋向于定值1/3曲边三角形面积S的最终值为多少?2.计算结果:分割以直代曲作和逼近3. 探究流程:S1五.定积分的定义积分上限积分下限:符号说明S1六. 定积分的几何意义---面积?回顾物理:根据v-t图象,回答问题Q:物体运动中,6s内的位移? A1+A3+A5+(-A2)+(-A4)---带“正负”的面积x轴上方——“正”面积x轴下方——“负”面积思考: 小 结 微积分是现代数学的基础
定积分是用极限逼近思想求曲边梯形的面积,是一种“以直代曲”数学转化思想的体现,它充分体现了对立与统一,量变与质变的辨证关系,体现了学科交叉渗透和中学与大学的衔接。 小 结
高中数学教研组赛课
“团结协作 拼搏创新”——高中数学教研组团队赛课流程团队上课代表张依老师上课团队说课代表李志斌老师说课团队评课代表钟高介老师评课“聚焦课堂,提质增效”专家点评张依上课
《曲边梯形的面积与定积分》高中数学教研组 张 依
高一数学组 大学先修课
—曲边梯形面积与定积分 微积分基本定理2019-12-301例1 根据v-t图象,回答以下问题: 一.情景引入Q:物体运动中,4s内的位移问题一: 我们生活与工程实际中经常接触的物体变速运动v-t图象大都是曲线,此时位移面积怎么计算呢? 二.提出问题问题二: 求曲边梯形的面积(为简化问题,我们以曲边三角形为例进行研究)
求直线x?0、x?1、x轴及曲线y?x2所围成的曲边三角形的面积S?三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积三.小组合作---计算曲边梯形面积Q1: 结合“割圆术”,思考如何估算曲边三角形的面积?S1以直代曲方案1方案2方案311Q2: 以下分隔代替方式中,你会选择哪个方案来进行计算?均分将大曲边三角形等分为 n 个小曲边梯形 ,并将每个小曲边梯形面积用小矩形代替: 每个小矩形的宽:每个小矩形的面积:1.估算方案均匀分割+以直代曲三.小组合作---计算矩形面积和活动说明:
1.每3个组计算一种分割情况——矩形分割个数分别分5,10,20
2.学案已做好分隔,利用表格进行数据的整理,并使用公式和计算器计算,最终面积和结果精确到小数点后4位,计算完后,成员相互分享一下答案,确定最终发表结果。
3.计算时注意所给区间是[0,1]。
Q3: 当分割越细,即份数n无限增大时,矩形面积和与曲边三角形面积S有什么关系?当份数n无限增大时,矩形面积和无限逼近曲边三角形面积SS趋向于定值1/3曲边三角形面积S的最终值为多少?2.计算结果:分割以直代曲作和逼近3. 探究流程:S1五.定积分的定义积分上限积分下限:符号说明S1六. 定积分的几何意义---面积?回顾物理:根据v-t图象,回答问题Q:物体运动中,6s内的位移? A1+A3+A5+(-A2)+(-A4)---带“正负”的面积x轴上方——“正”面积x轴下方——“负”面积思考: 小 结 微积分是现代数学的基础
定积分是用极限逼近思想求曲边梯形的面积,是一种“以直代曲”数学转化思想的体现,它充分体现了对立与统一,量变与质变的辨证关系,体现了学科交叉渗透和中学与大学的衔接。 小 结
