1.5.3 定积分的概念 课件23张PPT
文档属性
| 名称 | 1.5.3 定积分的概念 课件23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 479.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:12:43 | ||
图片预览



文档简介
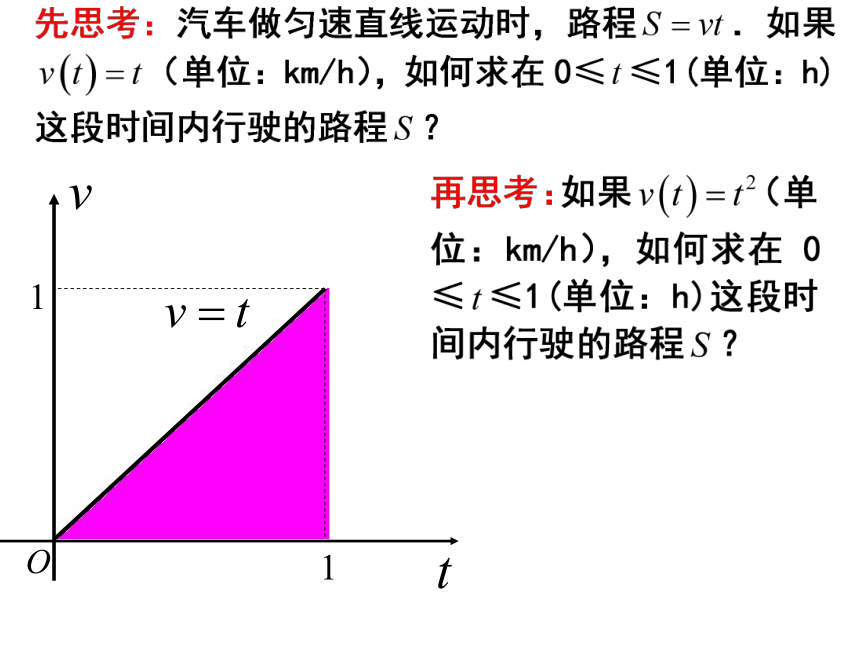
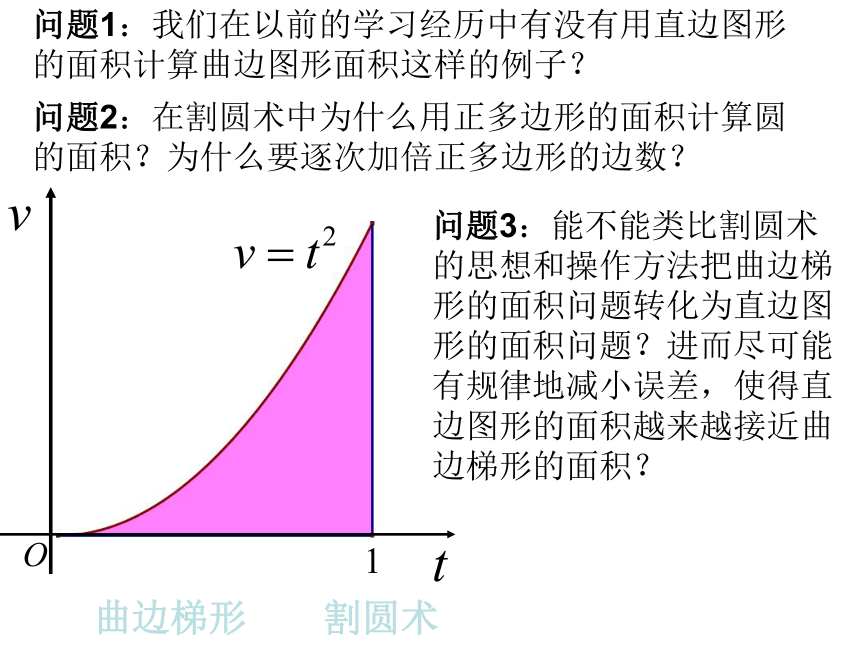
课件23张PPT。普通高中课程标准实验教科书 数学 选修 2-2 第一章 1.5.1节定积分的概念问题1:我们在以前的学习经历中有没有用直边图形的面积计算曲边图形面积这样的例子? 曲边梯形割圆术问题2:在割圆术中为什么用正多边形的面积计算圆的面积?为什么要逐次加倍正多边形的边数? 问题3:能不能类比割圆术的思想和操作方法把曲边梯形的面积问题转化为直边图形的面积问题?进而尽可能有规律地减小误差,使得直边图形的面积越来越接近曲边梯形的面积? 方案展示 思考、讨论,进行交流问题4:请比较不同方案的区别,哪种方案既实现了“以直代曲”,和“无限逼近”,又更便于实际操作? 例1.求由直线 与抛物线
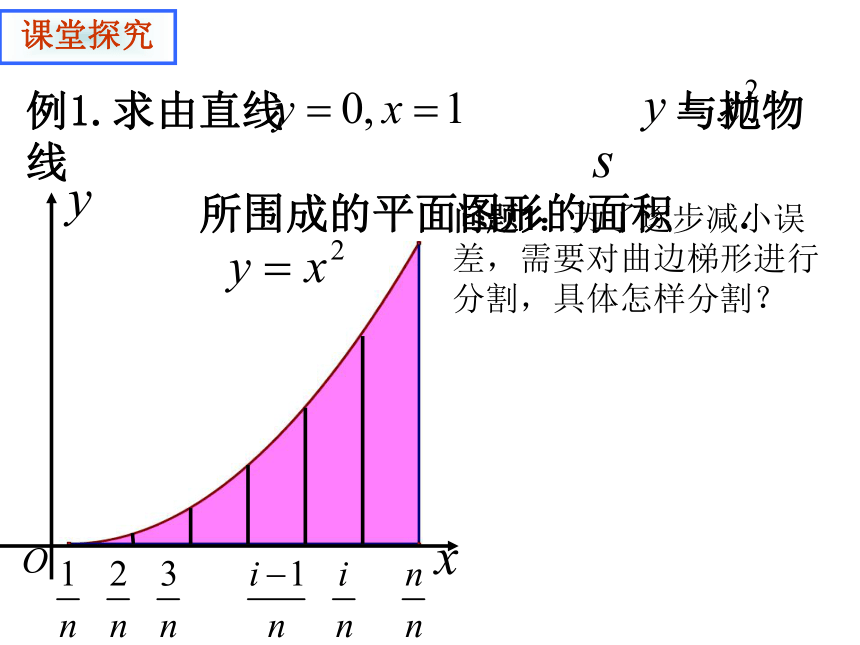
所围成的平面图形的面积 .课堂探究问题1:为了逐步减小误差,需要对曲边梯形进行分割,具体怎样分割?例1.求由直线 与抛物线
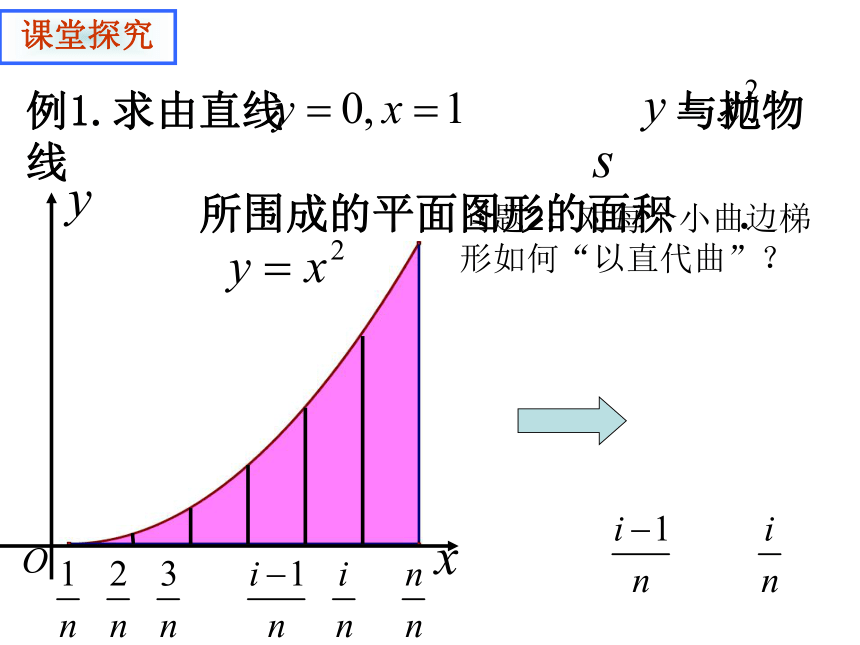
所围成的平面图形的面积 .课堂探究问题2:对每个小曲边梯形如何“以直代曲”?例1.求由直线 与抛物线
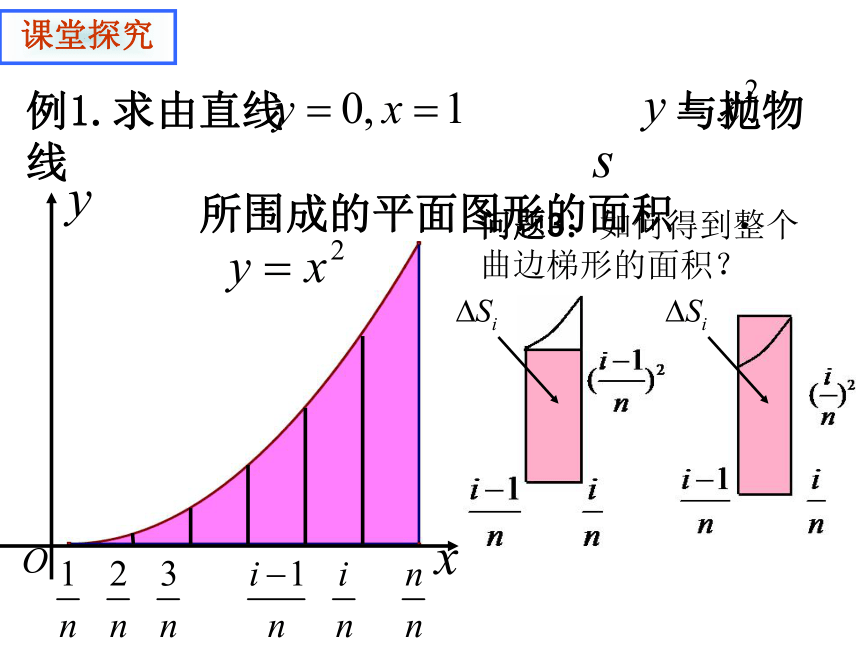
所围成的平面图形的面积 .课堂探究问题3:如何得到整个曲边梯形的面积?例1.求由直线 与抛物线
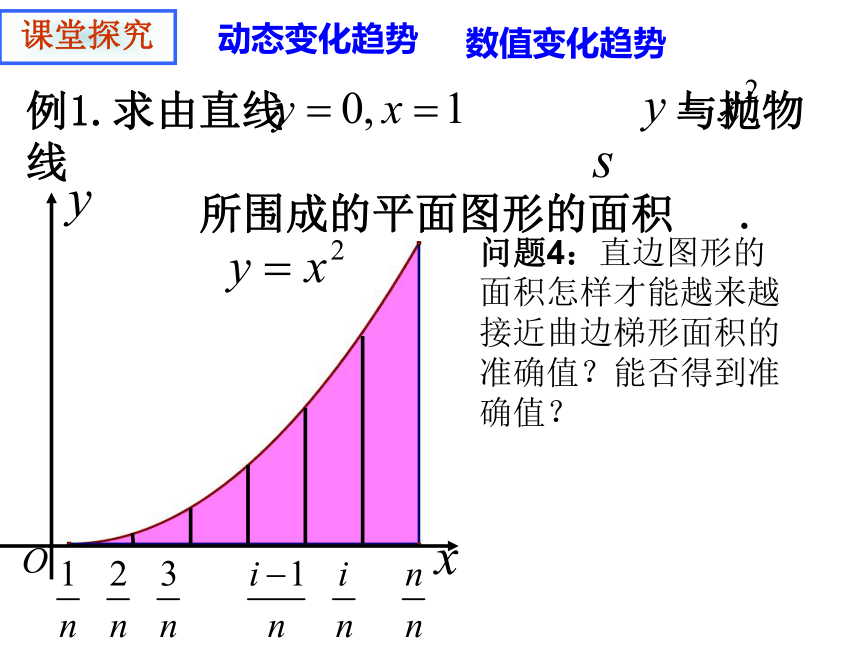
所围成的平面图形的面积 .动态变化趋势数值变化趋势课堂探究问题4:直边图形的面积怎样才能越来越接近曲边梯形面积的准确值?能否得到准确值?问题6:回顾求曲边梯形面积的整个过程,你能概括出求这个曲边梯形面积的方法吗?分割近似代替求和取极限以直代曲无限逼近定积分的定义:记为积分下限积分上限 在十六世纪,有许多科学问题需要解决,由于航海、机械制造、军事上的需要,运动的研究成了自然科学的中心议题,于是在数学中开始研究各种变化过程中的量(变量)之间的依赖关系,变量的引进,形成了数学中的转折点。数学史链接:微积分的发展 第一类是研究物体运动的时候直接出现的,也就是求瞬时速度的问题。第二类问题是求曲线的切线的问题。十七世纪中叶其他科学提出的四种亟待解决的数学问题:
第三类问题是求函数的最大值和最小值问题。 第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心、一个体积相当大的物体作用于另一物体上的引力。 微积分的发展极大的推动了数学的发展,同时在物理、化学、生物、天文、地理以及经济等各种科学领域中都有非常广泛而重要的应用。
????? 微积分的产生和发展被誉为“近代技术文明产生的关键事件之一,它引入了若干极其成功的、对以后许多数学的发展起决定性作用的思想。”恩格斯称之为“17世纪自然科学的三大发明之一”。1.定积分的实质?2.定积分的思想和方法?特殊和式的极限.求近似以直代曲取极限小 结 1.求由直线 和曲线 所围成的图形的面积S.作 业3.思考:定积分的几何意义是什么?下课刘徽割圆术割之弥细
失之弥少
割之又割
以至于不可割
则与圆合体
而无所失矣高明的逼近方法返回返回方案展示 返回不足近似过剩近似
所围成的平面图形的面积 .课堂探究问题1:为了逐步减小误差,需要对曲边梯形进行分割,具体怎样分割?例1.求由直线 与抛物线
所围成的平面图形的面积 .课堂探究问题2:对每个小曲边梯形如何“以直代曲”?例1.求由直线 与抛物线
所围成的平面图形的面积 .课堂探究问题3:如何得到整个曲边梯形的面积?例1.求由直线 与抛物线
所围成的平面图形的面积 .动态变化趋势数值变化趋势课堂探究问题4:直边图形的面积怎样才能越来越接近曲边梯形面积的准确值?能否得到准确值?问题6:回顾求曲边梯形面积的整个过程,你能概括出求这个曲边梯形面积的方法吗?分割近似代替求和取极限以直代曲无限逼近定积分的定义:记为积分下限积分上限 在十六世纪,有许多科学问题需要解决,由于航海、机械制造、军事上的需要,运动的研究成了自然科学的中心议题,于是在数学中开始研究各种变化过程中的量(变量)之间的依赖关系,变量的引进,形成了数学中的转折点。数学史链接:微积分的发展 第一类是研究物体运动的时候直接出现的,也就是求瞬时速度的问题。第二类问题是求曲线的切线的问题。十七世纪中叶其他科学提出的四种亟待解决的数学问题:
第三类问题是求函数的最大值和最小值问题。 第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心、一个体积相当大的物体作用于另一物体上的引力。 微积分的发展极大的推动了数学的发展,同时在物理、化学、生物、天文、地理以及经济等各种科学领域中都有非常广泛而重要的应用。
????? 微积分的产生和发展被誉为“近代技术文明产生的关键事件之一,它引入了若干极其成功的、对以后许多数学的发展起决定性作用的思想。”恩格斯称之为“17世纪自然科学的三大发明之一”。1.定积分的实质?2.定积分的思想和方法?特殊和式的极限.求近似以直代曲取极限小 结 1.求由直线 和曲线 所围成的图形的面积S.作 业3.思考:定积分的几何意义是什么?下课刘徽割圆术割之弥细
失之弥少
割之又割
以至于不可割
则与圆合体
而无所失矣高明的逼近方法返回返回方案展示 返回不足近似过剩近似
