1.5.3 定积分的概念 课件 25张PPT
文档属性
| 名称 | 1.5.3 定积分的概念 课件 25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 504.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:13:35 | ||
图片预览







文档简介
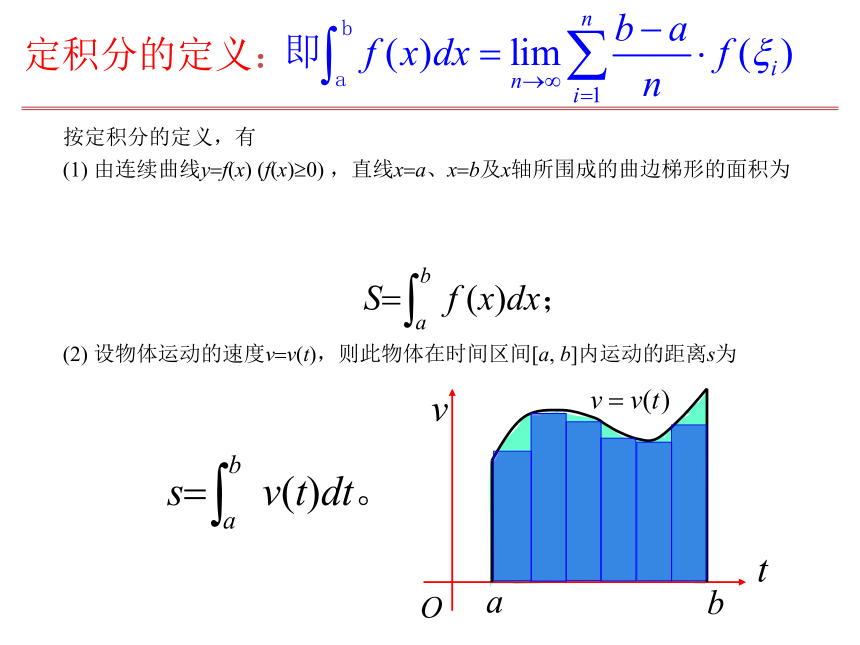
课件25张PPT。1.5.3定积分的概念 从求曲边梯形面积以及变速直线运动路程的过程可知,它们都可以通过“四步曲”:分割、近似代替、求和、取极限得到解决,且都可以归结为求一个特定形式和的极限.知识回顾 求由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积。 引例:曲边梯形的面积(i)分割:(ii)近似代替:(iii)求和:(iv)取极限:定 积 分自主交流,合作探究一、定积分的概念归纳总结形成概念定积分的定义: 定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。 按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为 (2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为定积分的定义:1 3.定积分的值与积分变量用什么字母表示无关,即有
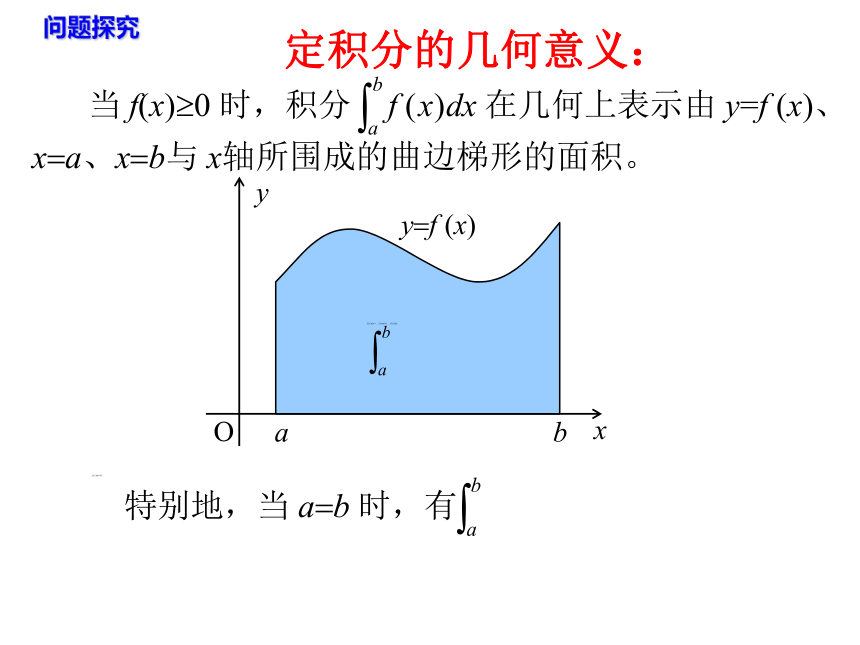
说明 x=a、x=b与 x轴所围成的曲边梯形的面积。定积分的几何意义:问题探究 当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,上述曲边梯形面积的负值。 曲边梯形的面积曲边梯形的面积的相反数也就是:根据定积分的几何意义,你能用定积分表示图中阴影部分的面积吗?问题探究 定积分的基本性质 性质1. 性质2. 定积分关于积分区间具有可加性性质3. (1)分割例题分析(2)近似代替,作和(3)取极限例2、利用定积分的几何意义,求下列各式的值.分析:定积分 的几何意义是:介于直线x=a,x=b,x轴及y=f(x)所围成图形面积的代数和,其中x轴上方部分为正,x轴下方部分为负.被积函数的曲线是圆心在原点,半径为2的半圆,
由定积分的几何意义知,此定积分为半圆的面积,
所以 解:xyf(x)=sinx1-1例2、利用定积分的几何意义,求下列各式的值.1.定积分的概念。2.定积分的几何意义: 曲边梯形的面积 (或面积的相反数)3、定积分的基本性质。4、定积分的求法。2-2[-2,2]0A课堂练习5:用定积分表示下列阴影部分的面积. (1)S=________. 课堂练习 (2)S=________. (3)S=________.课后作业课本P50页 A组5题 、B组3题
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。 按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为 (2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为定积分的定义:1 3.定积分的值与积分变量用什么字母表示无关,即有
说明 x=a、x=b与 x轴所围成的曲边梯形的面积。定积分的几何意义:问题探究 当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,上述曲边梯形面积的负值。 曲边梯形的面积曲边梯形的面积的相反数也就是:根据定积分的几何意义,你能用定积分表示图中阴影部分的面积吗?问题探究 定积分的基本性质 性质1. 性质2. 定积分关于积分区间具有可加性性质3. (1)分割例题分析(2)近似代替,作和(3)取极限例2、利用定积分的几何意义,求下列各式的值.分析:定积分 的几何意义是:介于直线x=a,x=b,x轴及y=f(x)所围成图形面积的代数和,其中x轴上方部分为正,x轴下方部分为负.被积函数的曲线是圆心在原点,半径为2的半圆,
由定积分的几何意义知,此定积分为半圆的面积,
所以 解:xyf(x)=sinx1-1例2、利用定积分的几何意义,求下列各式的值.1.定积分的概念。2.定积分的几何意义: 曲边梯形的面积 (或面积的相反数)3、定积分的基本性质。4、定积分的求法。2-2[-2,2]0A课堂练习5:用定积分表示下列阴影部分的面积. (1)S=________. 课堂练习 (2)S=________. (3)S=________.课后作业课本P50页 A组5题 、B组3题
