1.5 函数的极值与导数(一)课件30张PPT
文档属性
| 名称 | 1.5 函数的极值与导数(一)课件30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 959.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:18:01 | ||
图片预览








文档简介
课件30张PPT。 函数的
极值与导数
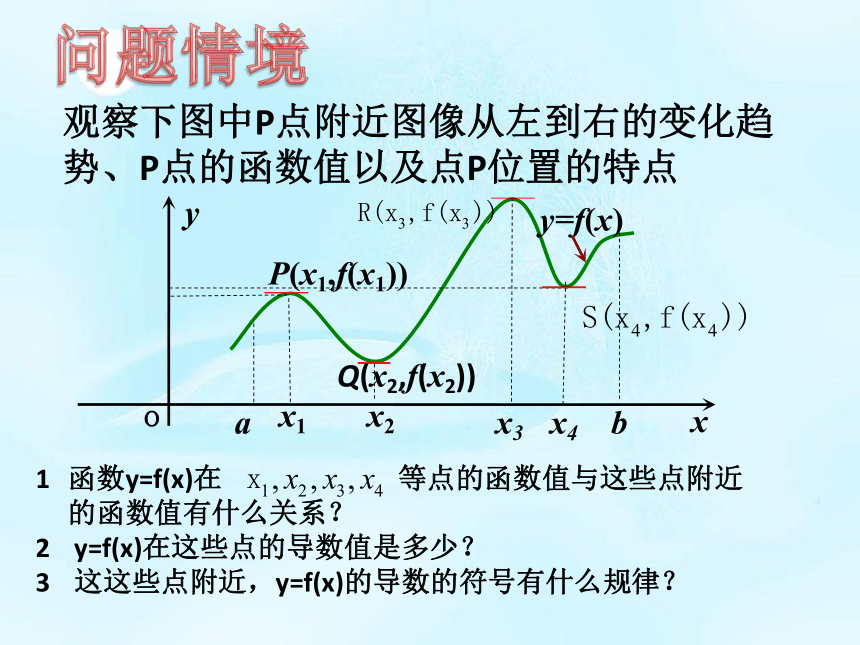
(一)观察下图中P点附近图像从左到右的变化趋势、P点的函数值以及点P位置的特点问题情境函数y=f(x)在 等点的函数值与这些点附近的函数值有什么关系?
y=f(x)在这些点的导数值是多少?
这这些点附近,y=f(x)的导数的符号有什么规律? 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)﹤f (x0),我们就说f (x0)是函数f(x)的一个极大值,记作y极大值= f (x0);如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
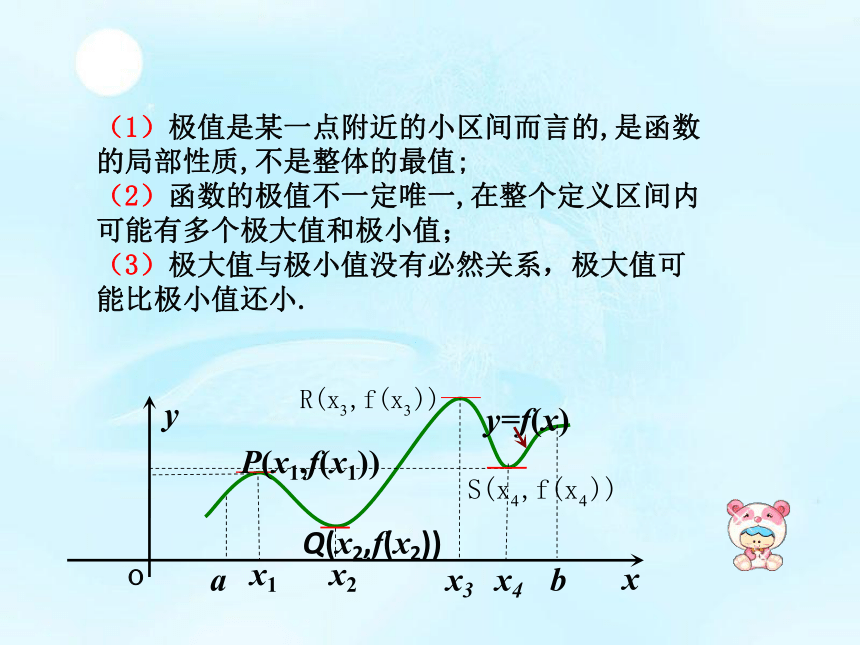
极大值与极小值同称为极值. 函数极值的定义(1)极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
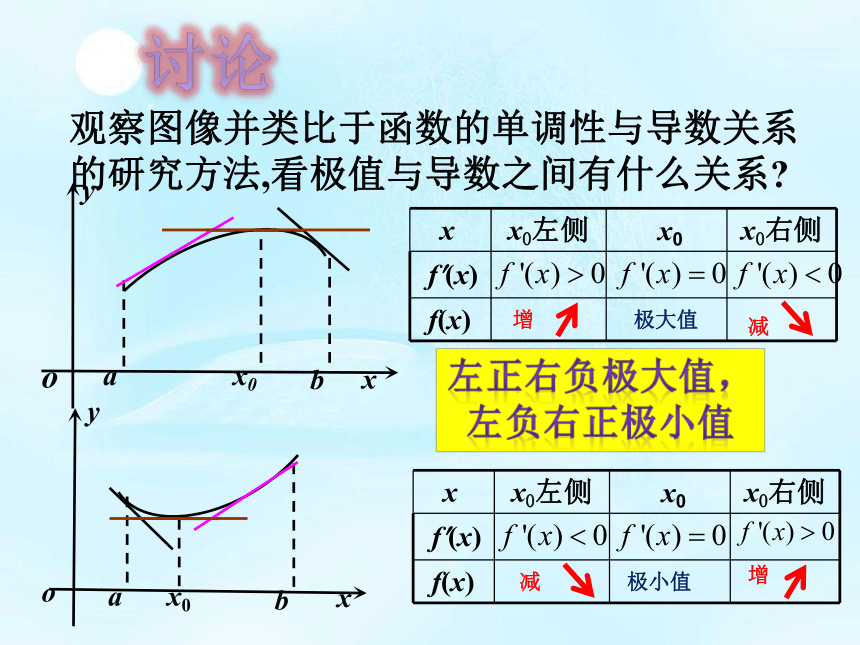
(3)极大值与极小值没有必然关系,极大值可能比极小值还小. 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?讨论增增减减极大值极小值左正右负极大值,
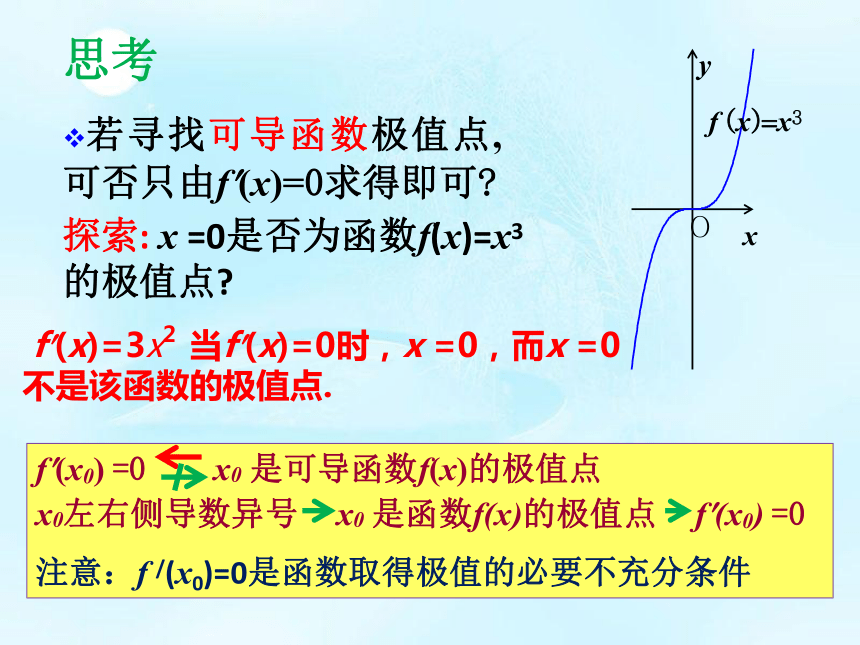
左负右正极小值若寻找可导函数极值点,可否只由f?(x)=0求得即可?思考探索: x =0是否为函数f(x)=x3
的极值点? f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.f?(x0) =0 x0 是可导函数f(x)的极值点
x0左右侧导数异号 x0 是函数f(x)的极值点 f?(x0) =0
注意:f /(x0)=0是函数取得极值的必要不充分条件函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习注意:极值点指的是自变量x,
极值指的是函数值y例1例2所以,当x=-1是,函数的极大值是-2,当x=1时,函数的极小值是2导函数的正负是
交替出现的吗?不是求可导函数极值的步骤:练习课堂小结1、极值的判定方法
2、极值的求法注意:
1、f /(x0)=0是函数取得极值的必要不充分条件
2、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号. 函数的
极值与导数
(二)题型 1:图像与函数的极值12 导函数y=f’(x)的图像如图,试找出函数y=f(x)的极值点,并指出那些是极大值点,那些是极小值点?XYOax1x2x3x4x5x6bY=f’(x)X2,x4为极值点
X2为极大值点
X4为极小值点3 导函数y=f’(x)的图像如图,在标记的点中哪一点处
(1)导函数y=f’(x)有极大值?
(2)导函数y=f’(x)有极小值?
(3)函数y=f(x)有极大值?
(4)函数y=f(x)有极小值?
x1x2x3x4Y=f’(x)XYOX2X4X3x5X5已知汽车在笔直的公路上行驶:
(1)如果函数y=f(x)表示时刻t时汽车与起点的距离,请标出汽车速度等于0的点
(2)如果函数y=f(x)表示时刻t时汽车的速度,那么(1)中标出点的意义是什么?y=f(t)5 以下图形分别表示一个三次函数及其导数在同一坐标系中的图像,其中一定不正确的序号是( )XYOXYOXYOXYO(1)(2)(3)(4)A (3)(4) B (1)(3) C (2)(4) D(1)(2)A题型2:含参数的函数分析:如果函数有极大值又有极小值,说明函数的导数的符号有从正变到负和从负变到正的时候,也就是说到导函数有两个相异的实根2 若不等式 对任意实数x都成立,求实数a的取值范围分析:由不等式可以知道 ,则要求a的范围,只要a 大于函数 的最大值即可,问题转化成求函数f(x)的最值课堂小结1 通过图像来观察函数的极值点
2 利用极值与导数的关系来求函数中参数的范围 函数的
极值与导数
(三)目标:
根据函数的极值与函数的导数关系来求解函数的解析式
数形结合来解决问题
例1题型3: 求解析式若函数 在x=-1和x=3时有极值,则a=_______,b=_______-3-9a=-3,b=-9,c=2,极小值为-25 (2006年北京卷)已知函数在点 处取得极大值5,其导函数 的图像(如图)过点(1,0),(2,0), 求:
(1) 的值;(2)a,b,c的值;(1)由图像可知:(2) 在x=2处有极大值,求常数c的值 C=6
极值与导数
(一)观察下图中P点附近图像从左到右的变化趋势、P点的函数值以及点P位置的特点问题情境函数y=f(x)在 等点的函数值与这些点附近的函数值有什么关系?
y=f(x)在这些点的导数值是多少?
这这些点附近,y=f(x)的导数的符号有什么规律? 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)﹤f (x0),我们就说f (x0)是函数f(x)的一个极大值,记作y极大值= f (x0);如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
极大值与极小值同称为极值. 函数极值的定义(1)极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(3)极大值与极小值没有必然关系,极大值可能比极小值还小. 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?讨论增增减减极大值极小值左正右负极大值,
左负右正极小值若寻找可导函数极值点,可否只由f?(x)=0求得即可?思考探索: x =0是否为函数f(x)=x3
的极值点? f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.f?(x0) =0 x0 是可导函数f(x)的极值点
x0左右侧导数异号 x0 是函数f(x)的极值点 f?(x0) =0
注意:f /(x0)=0是函数取得极值的必要不充分条件函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习注意:极值点指的是自变量x,
极值指的是函数值y例1例2所以,当x=-1是,函数的极大值是-2,当x=1时,函数的极小值是2导函数的正负是
交替出现的吗?不是求可导函数极值的步骤:练习课堂小结1、极值的判定方法
2、极值的求法注意:
1、f /(x0)=0是函数取得极值的必要不充分条件
2、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号. 函数的
极值与导数
(二)题型 1:图像与函数的极值12 导函数y=f’(x)的图像如图,试找出函数y=f(x)的极值点,并指出那些是极大值点,那些是极小值点?XYOax1x2x3x4x5x6bY=f’(x)X2,x4为极值点
X2为极大值点
X4为极小值点3 导函数y=f’(x)的图像如图,在标记的点中哪一点处
(1)导函数y=f’(x)有极大值?
(2)导函数y=f’(x)有极小值?
(3)函数y=f(x)有极大值?
(4)函数y=f(x)有极小值?
x1x2x3x4Y=f’(x)XYOX2X4X3x5X5已知汽车在笔直的公路上行驶:
(1)如果函数y=f(x)表示时刻t时汽车与起点的距离,请标出汽车速度等于0的点
(2)如果函数y=f(x)表示时刻t时汽车的速度,那么(1)中标出点的意义是什么?y=f(t)5 以下图形分别表示一个三次函数及其导数在同一坐标系中的图像,其中一定不正确的序号是( )XYOXYOXYOXYO(1)(2)(3)(4)A (3)(4) B (1)(3) C (2)(4) D(1)(2)A题型2:含参数的函数分析:如果函数有极大值又有极小值,说明函数的导数的符号有从正变到负和从负变到正的时候,也就是说到导函数有两个相异的实根2 若不等式 对任意实数x都成立,求实数a的取值范围分析:由不等式可以知道 ,则要求a的范围,只要a 大于函数 的最大值即可,问题转化成求函数f(x)的最值课堂小结1 通过图像来观察函数的极值点
2 利用极值与导数的关系来求函数中参数的范围 函数的
极值与导数
(三)目标:
根据函数的极值与函数的导数关系来求解函数的解析式
数形结合来解决问题
例1题型3: 求解析式若函数 在x=-1和x=3时有极值,则a=_______,b=_______-3-9a=-3,b=-9,c=2,极小值为-25 (2006年北京卷)已知函数在点 处取得极大值5,其导函数 的图像(如图)过点(1,0),(2,0), 求:
(1) 的值;(2)a,b,c的值;(1)由图像可知:(2) 在x=2处有极大值,求常数c的值 C=6
