1.5.3 定积分的概念课件23张PPT
文档属性
| 名称 | 1.5.3 定积分的概念课件23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 993.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:19:58 | ||
图片预览








文档简介
课件23张PPT。 定积分的概念考纲展示
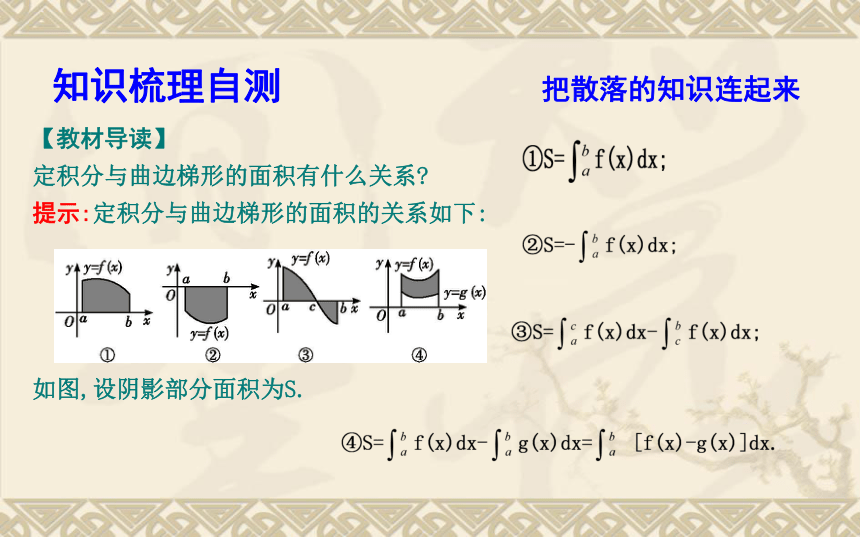
1.了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念. 2.了解微积分基本定理的含义. 知识梳理自测 把散落的知识连起来【教材导读】
定积分与曲边梯形的面积有什么关系?提示:定积分与曲边梯形的面积的关系如下:如图,设阴影部分面积为S.知识梳理 积分下限 积分上限 积分区间 被积函数 x f(x)dx x=a,x=b(a≠b),y=0A1+A3-A2-A42.微积分基本定理(牛顿-莱布尼茨公式)
定理所满足的条件
①f(x)是区间[a,b]上的连续函数;F′(x)F(b)-F(a)【重要结论】
设函数f(x)在闭区间[-a,a]上连续,则有双基自测 (A)a(C)c(2)运用微积分基本定理求定积分时要注意以下几点:
①对被积函数要先化简,再求积分.
②求被积函数为分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和.
③对于含有绝对值符号的被积函数,要先去掉绝对值号再求积分.
④注意用“F′(x)=f(x)”检验积分的对错.
提醒:被积函数若含有绝对值号,应先去绝对值号,再分段积分.答案:(3)2 (4)1考点二 应用定积分求面积【例2】 (1)直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )答案:(1)C(2)已知曲线y=x2与直线y=kx(k>0)所围成的曲边图形的面积为 ,则k=
.?答案:(2)2反思归纳 (1)利用定积分求曲边梯形面积的步骤:
①画出曲线的草图.
②借助图形,确定被积函数,求出交点坐标,确定积分的上、下限.
③将“曲边梯形”的面积表示成若干个定积分的和或差.
④计算定积分,写出答案.
(2)利用定积分求面积时注意选择合适的积分变量以简化运算.(2)已知函数f(x)=x3-x2+x+1,求其在点(1,2)处的切线与函数g(x)=x2围成的图形的面积为 .?
1.了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念. 2.了解微积分基本定理的含义. 知识梳理自测 把散落的知识连起来【教材导读】
定积分与曲边梯形的面积有什么关系?提示:定积分与曲边梯形的面积的关系如下:如图,设阴影部分面积为S.知识梳理 积分下限 积分上限 积分区间 被积函数 x f(x)dx x=a,x=b(a≠b),y=0A1+A3-A2-A42.微积分基本定理(牛顿-莱布尼茨公式)
定理所满足的条件
①f(x)是区间[a,b]上的连续函数;F′(x)F(b)-F(a)【重要结论】
设函数f(x)在闭区间[-a,a]上连续,则有双基自测 (A)a
①对被积函数要先化简,再求积分.
②求被积函数为分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和.
③对于含有绝对值符号的被积函数,要先去掉绝对值号再求积分.
④注意用“F′(x)=f(x)”检验积分的对错.
提醒:被积函数若含有绝对值号,应先去绝对值号,再分段积分.答案:(3)2 (4)1考点二 应用定积分求面积【例2】 (1)直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )答案:(1)C(2)已知曲线y=x2与直线y=kx(k>0)所围成的曲边图形的面积为 ,则k=
.?答案:(2)2反思归纳 (1)利用定积分求曲边梯形面积的步骤:
①画出曲线的草图.
②借助图形,确定被积函数,求出交点坐标,确定积分的上、下限.
③将“曲边梯形”的面积表示成若干个定积分的和或差.
④计算定积分,写出答案.
(2)利用定积分求面积时注意选择合适的积分变量以简化运算.(2)已知函数f(x)=x3-x2+x+1,求其在点(1,2)处的切线与函数g(x)=x2围成的图形的面积为 .?
