2.3 数学归纳法课件22张PPT
文档属性
| 名称 | 2.3 数学归纳法课件22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:24:41 | ||
图片预览








文档简介
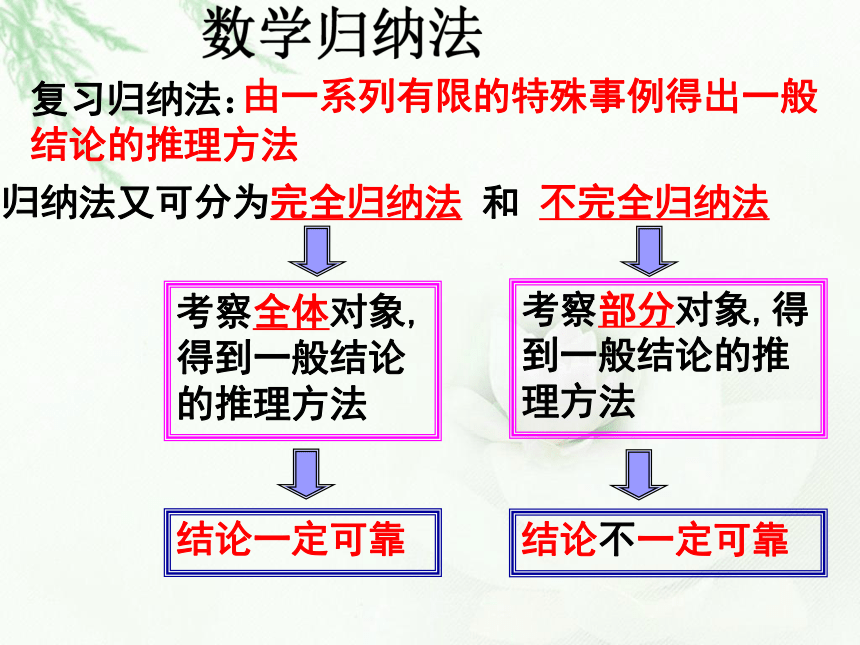
课件22张PPT。含中欢迎您!!市级公开课复习归纳法:结论一定可靠结论不一定可靠考察全体对象,得到一般结论的推理方法考察部分对象,得到一般结论的推理方法归纳法又可分为完全归纳法 和 不完全归纳法 由一系列有限的特殊事例得出一般结论的推理方法 可从简单情形出发观察、归纳、猜想(不完全归纳法)费马(Fermat) 曾经提出一个猜想:形如Fn=22n+1(n=0,1,2…)的数都是质数……100年后… 费马(1601--1665)法国伟大的业余数学家。 欧拉(1707~1783),瑞士数学家及自然科学家。 费马您错了!不完全归纳法能帮助我们发现猜想,但不能保证猜想正确. 其中道理可用于数学证明──数学归纳法.这种一种严格的证明方法──数学归纳法. 1.验证第一个命题成立(即n=n0第一个命题对应的n的值,如n0=1);
2.假设当n=k时命题成立,证明当n=k+1时命题也成立.(归纳奠基)数学归纳法: 关于正整数n的命题(相当于多米诺骨牌),我们可以采用下面方法来证明其正确性: 由(1)、(2)知,对于一切n≥n0的自然数n都成立!(归纳递推)注意:运用数学归纳法证题,以上两步缺一不可.思考1:下面的推理是否正确?错在没有奠基等式思考2:下面用数学归纳法证明的过程是否正确:
错在第二步证明没有用上假设用上假设,递推才成立数学归纳法具体应用:例1.用数学归纳法证明:第二步证明是关键:1.要用到归纳假设作为理由.2.看清从k到k+1中间的变化.证明: (1) 当n=1时,左=1,右=12=1
∴n=1时,等式成立
(2) 假设n=k时,等式成立,即1+3+5+…+(2k?1)=k2
那么,当n=k+1时
左=1+3+5+…+(2k?1)+[2(k+1)-1]
=k2+2k+1
=(k+1)2=右
即n=k+1时等式成立
由(1)、(2)可知等式对任何n?N*都成立递推基础递推依据例2、用数学归纳法证明:证明: (1) 当n=1时,左=1,右=12=1
∴n=1时,等式成立
(2) 假设n=k时,等式成立,当n=k+1时,根据(1)和(2)可以断定,变式:用数学归纳法证明
课堂练习:
课本第95页练习1,2.数学归纳法是一种证明与自然数有关的数学命题的重要方法。其格式主要有两个步骤、一个结论:
(1)证明当n取第一个值n0(如 n0=1或2等)时结论正确;
验证初始条件
(2)假设n=k时结论正确,在假设之下,证明n=k+1时结论也正确;
假设推理
(3)由(1)、(2)得出结论.
下结论2.“观察、猜想、证明”是解决与自然数有关的命题的有效途径.注意:递推基础不可少,归纳假设要用到,结论写明莫忘掉。课堂小结:找准起点,奠基要稳用上假设
递推才真写明结论
才算完整课后作业:1.课本第96页A组第一大题.THANKS!>>谢谢观看
2.假设当n=k时命题成立,证明当n=k+1时命题也成立.(归纳奠基)数学归纳法: 关于正整数n的命题(相当于多米诺骨牌),我们可以采用下面方法来证明其正确性: 由(1)、(2)知,对于一切n≥n0的自然数n都成立!(归纳递推)注意:运用数学归纳法证题,以上两步缺一不可.思考1:下面的推理是否正确?错在没有奠基等式思考2:下面用数学归纳法证明的过程是否正确:
错在第二步证明没有用上假设用上假设,递推才成立数学归纳法具体应用:例1.用数学归纳法证明:第二步证明是关键:1.要用到归纳假设作为理由.2.看清从k到k+1中间的变化.证明: (1) 当n=1时,左=1,右=12=1
∴n=1时,等式成立
(2) 假设n=k时,等式成立,即1+3+5+…+(2k?1)=k2
那么,当n=k+1时
左=1+3+5+…+(2k?1)+[2(k+1)-1]
=k2+2k+1
=(k+1)2=右
即n=k+1时等式成立
由(1)、(2)可知等式对任何n?N*都成立递推基础递推依据例2、用数学归纳法证明:证明: (1) 当n=1时,左=1,右=12=1
∴n=1时,等式成立
(2) 假设n=k时,等式成立,当n=k+1时,根据(1)和(2)可以断定,变式:用数学归纳法证明
课堂练习:
课本第95页练习1,2.数学归纳法是一种证明与自然数有关的数学命题的重要方法。其格式主要有两个步骤、一个结论:
(1)证明当n取第一个值n0(如 n0=1或2等)时结论正确;
验证初始条件
(2)假设n=k时结论正确,在假设之下,证明n=k+1时结论也正确;
假设推理
(3)由(1)、(2)得出结论.
下结论2.“观察、猜想、证明”是解决与自然数有关的命题的有效途径.注意:递推基础不可少,归纳假设要用到,结论写明莫忘掉。课堂小结:找准起点,奠基要稳用上假设
递推才真写明结论
才算完整课后作业:1.课本第96页A组第一大题.THANKS!>>谢谢观看
