3.1.2 复数的几何意义课件21张PPT
文档属性
| 名称 | 3.1.2 复数的几何意义课件21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 210.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:31:03 | ||
图片预览






文档简介
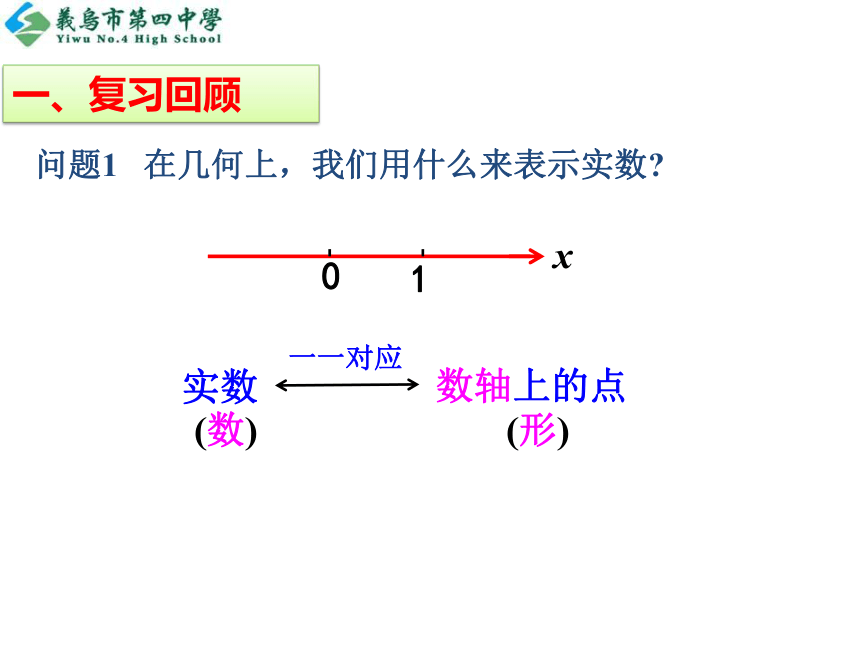
课件21张PPT。3.1.2 复数的几何意义普通高中人教A版数学选修2-2x01问题1 在几何上,我们用什么来表示实数?一、复习回顾实部虚部(a, b∈R)问题2 复数的代数形式是什么?一个复数可由什么确定?问题3 类比实数的几何意义,复数的几何意义是什么呢?复数z=a+bi有序实数对(a,b)一一对应一一对应探究点1 复数的几何表示二、新知探究Z(a,b) 建立了平面直角坐标系来表示复数的平面——复平面x轴——实轴y轴——虚轴z=a+bi思考:在复平面上,实轴上的点,
虚轴上的点,各象限内的点分别
表示什么样的数?(1)实轴上的点表示实数;
(2)虚轴上的点除原点外都表示纯虚数;
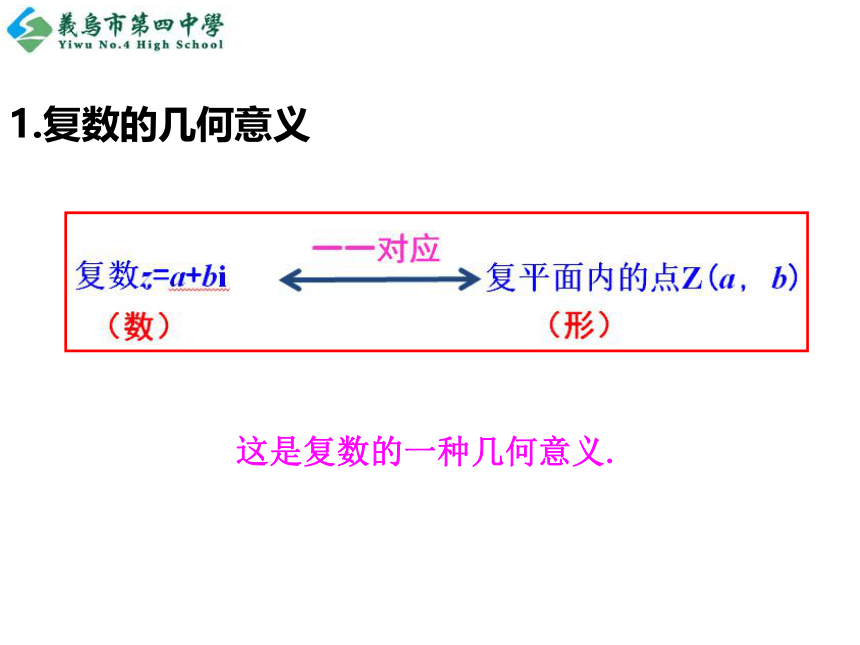
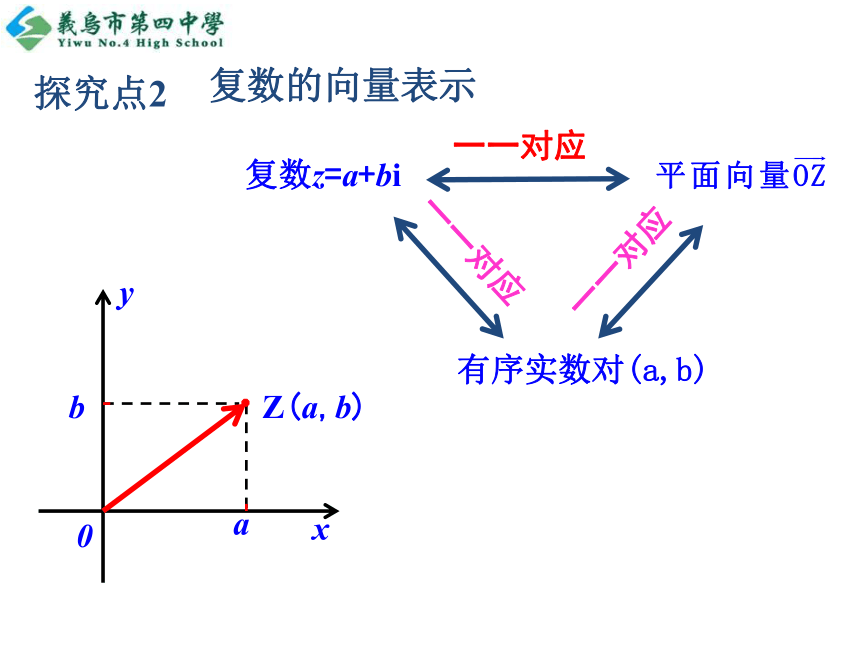
(3)各象限内的点表示实部和虚部都不为零的虚数. 复数的这种几何表示于1797年由挪威的测量学家韦塞尔提出,随即由瑞士的藏书家阿甘得出书进行讨论并得到高斯的认同,因此这种几何表示也称阿甘得图。这是复数的一种几何意义.1.复数的几何意义口答:在复平面上,下列各点对应哪个复数?(1)原点(0,0)表示 ;(2)实轴上的点(2,0)表示 ;(3)虚轴上的点(0,-1)表示 ;(4)点(-2,3)表示 。实数0实数2纯虚数-i复数-2+3i复数z=a+bi探究点2 复数的向量表示一一对应Z(a,b)这是复数的又一种几何意义.Z(a,b)z=a+bi2.复数的模 当b=0时,复数z=a+bi是一个实数a,
它的模等于|a|(就是a的绝对值)。 复数 z=a+bi的模r就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.复数模的几何意义:(1)下列命题中的假命题是( )
A.在复平面内,对应于实数的点都在实轴上
B.在复平面内,对应于纯虚数的点都在虚轴上
C.在复平面内,实轴上的点所对应的复数都是实数
D.在复平面内,虚轴上的点所对应的复数都是纯虚数 D三、新知应用例1.概念辨析(2)“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件C例2.已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. 复数对应点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)【小结提升】-3(2)|z-2|=|z+4|
(3)|z-i|+|z+i| =4
四、课堂小结本节课你有哪些收获?1.数学知识:2.数学思想:(1)类比思想
(2)转化思想
(3)数学形结合思想(1)复数的几何意义
(2)复数的模五、课外作业1.必做题:课外作业A组;
2.选做题:课外作业B组.3. 拓展阅读:
书本P113《阅读与思考:代数基本定理》谢谢!
虚轴上的点,各象限内的点分别
表示什么样的数?(1)实轴上的点表示实数;
(2)虚轴上的点除原点外都表示纯虚数;
(3)各象限内的点表示实部和虚部都不为零的虚数. 复数的这种几何表示于1797年由挪威的测量学家韦塞尔提出,随即由瑞士的藏书家阿甘得出书进行讨论并得到高斯的认同,因此这种几何表示也称阿甘得图。这是复数的一种几何意义.1.复数的几何意义口答:在复平面上,下列各点对应哪个复数?(1)原点(0,0)表示 ;(2)实轴上的点(2,0)表示 ;(3)虚轴上的点(0,-1)表示 ;(4)点(-2,3)表示 。实数0实数2纯虚数-i复数-2+3i复数z=a+bi探究点2 复数的向量表示一一对应Z(a,b)这是复数的又一种几何意义.Z(a,b)z=a+bi2.复数的模 当b=0时,复数z=a+bi是一个实数a,
它的模等于|a|(就是a的绝对值)。 复数 z=a+bi的模r就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.复数模的几何意义:(1)下列命题中的假命题是( )
A.在复平面内,对应于实数的点都在实轴上
B.在复平面内,对应于纯虚数的点都在虚轴上
C.在复平面内,实轴上的点所对应的复数都是实数
D.在复平面内,虚轴上的点所对应的复数都是纯虚数 D三、新知应用例1.概念辨析(2)“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件C例2.已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. 复数对应点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)【小结提升】-3
(3)|z-i|+|z+i| =4
四、课堂小结本节课你有哪些收获?1.数学知识:2.数学思想:(1)类比思想
(2)转化思想
(3)数学形结合思想(1)复数的几何意义
(2)复数的模五、课外作业1.必做题:课外作业A组;
2.选做题:课外作业B组.3. 拓展阅读:
书本P113《阅读与思考:代数基本定理》谢谢!
