3.1.2 复数的几何意义课件21张PPT
文档属性
| 名称 | 3.1.2 复数的几何意义课件21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:32:41 | ||
图片预览







文档简介
课件21张PPT。3.1.2 复数的几何意义人教A版选修2-2温故知新1.复数的代数形式:实部虚部2.复数的分类:3.复数相等的条件:规定:如果两个复数的实部和虚部分别相等,
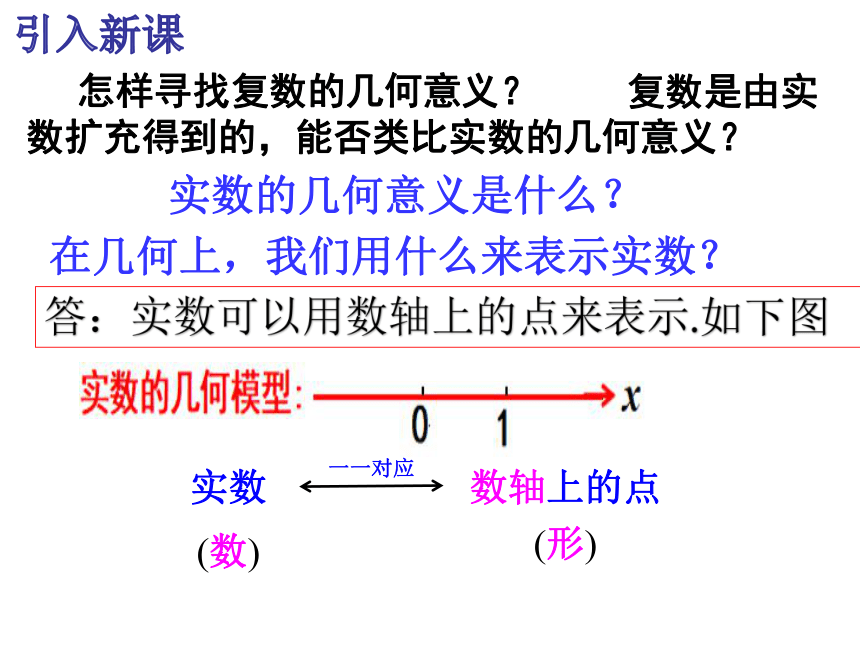
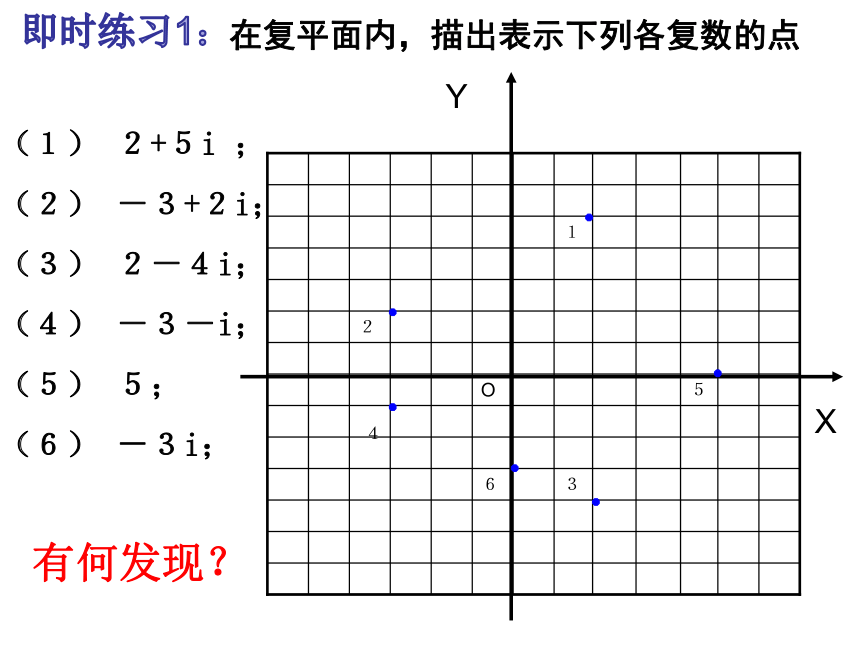
那么我们就说这两个复数相等. 1545年出现了负数开方问题.到了1637年,笛卡尔也认为负数开方是"不可思议的",称这样的数为"虚数"(虚数一词沿用至今).1799年高斯给出了复数的几何解释,使得复数没有那么虚无缥缈了.你知道高斯是怎样定义复数的几何解释的吗?法国数学家 笛卡尔德国数学家 高斯 复数是由实数扩充得到的,能否类比实数的几何意义?引入新课实数的几何意义是什么? 怎样寻找复数的几何意义?在几何上,我们用什么来表示实数?答:实数可以用数轴上的点来表示.如下图实数 数轴上的点 (形)(数)一一对应 思考:类比实数,在几何中,复数可以用什么来表示呢?实部虚部1、复数的几何意义(一)复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴------复数平面 (简称复平面)一一对应z=a+bi一一对应一一对应4365O21在复平面内,描出表示下列各复数的点XY(1) 2+5i ;
(2) -3+2i;
(3) 2-4i;
(4) -3-i;
(5) 5;
(6) -3i;即时练习1:有何发现?结论1、实轴上的点都表示实数;
2、除原点外,虚轴上的点都表示纯虚数。D2.“a=0”是复数a+bi (a,b∈R)是纯虚数”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件A例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. 变式:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值. 2、复数的几何意义(二)复数z=a+bi复平面内的点Z(a,b)一一对应一一对应一一对应xyobaZ(a,b)z=a+bi规定:相等的向量表示同一个复数O即时练习3:在复平面内,画出表示下列各复数对应的向量XY(1) 2+i ;
(2) -2+4i;
(3) -2i;
(4) 4;
(5) 1.5-4i;2+i -2+4i -2i 41.5-4i 小结一1.复数的代数形式:2.复数的几何形式:3.复数的向量形式:xyobaZ(a,b)z=a+bi3、复数的绝对值(也叫做复数的模)实数的绝对值在几何中
表示什么? |a|表示实数a在数轴上所对应的点A到原点O的距离.复数的绝对值在几何中表示什么呢?即时练习4 求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i
(4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)5 5 -5a 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个?(2)另解:设z=x+yi(x,y∈R)xyO11–1–1所以,复数|z|=1所对应
的点在复平面上构成一个以(0,0)为圆心,1为半径的圆。 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个? 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个? 复数|z-2|=1表示复数z=x+yi所对应的点(x,y)到点(2,0)的距离等于1,在复平面上构成一个以(2,0)为圆心,1为半径的圆。变式1:已知复数z满足|z-2|=1,
求|z-3-4i|的最小值和最大值。变式2:已知复数z对应点Z,求下列条件下动点Z(x,y)的轨迹。
(1)|z-i|+|z+i|=4
(2)|z-2|=|z+4|
复数z=a+bi的模|z|= ,从几何意义上理解,表示点Z(a,b)和原点间的距离;类比向量的模还可进一步引申:|z1-z2|表示复数z1和z2对应的点Z1和Z2之间的距离.
小结二知识点:思想方法:(1)类比思想(3)数形结合思想(2)转化思想1.复数的代数形式:2.复数的几何形式:3.复数的向量形式:本课总结4.复数模|z|:|z1-z2|表示复数z1和z2对应的点Z1和Z2之间的距离作业课本P106
A组 4.(1)(3);5.(2)
B组 1,3谢谢大家!
那么我们就说这两个复数相等. 1545年出现了负数开方问题.到了1637年,笛卡尔也认为负数开方是"不可思议的",称这样的数为"虚数"(虚数一词沿用至今).1799年高斯给出了复数的几何解释,使得复数没有那么虚无缥缈了.你知道高斯是怎样定义复数的几何解释的吗?法国数学家 笛卡尔德国数学家 高斯 复数是由实数扩充得到的,能否类比实数的几何意义?引入新课实数的几何意义是什么? 怎样寻找复数的几何意义?在几何上,我们用什么来表示实数?答:实数可以用数轴上的点来表示.如下图实数 数轴上的点 (形)(数)一一对应 思考:类比实数,在几何中,复数可以用什么来表示呢?实部虚部1、复数的几何意义(一)复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴------复数平面 (简称复平面)一一对应z=a+bi一一对应一一对应4365O21在复平面内,描出表示下列各复数的点XY(1) 2+5i ;
(2) -3+2i;
(3) 2-4i;
(4) -3-i;
(5) 5;
(6) -3i;即时练习1:有何发现?结论1、实轴上的点都表示实数;
2、除原点外,虚轴上的点都表示纯虚数。D2.“a=0”是复数a+bi (a,b∈R)是纯虚数”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件A例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. 变式:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值. 2、复数的几何意义(二)复数z=a+bi复平面内的点Z(a,b)一一对应一一对应一一对应xyobaZ(a,b)z=a+bi规定:相等的向量表示同一个复数O即时练习3:在复平面内,画出表示下列各复数对应的向量XY(1) 2+i ;
(2) -2+4i;
(3) -2i;
(4) 4;
(5) 1.5-4i;2+i -2+4i -2i 41.5-4i 小结一1.复数的代数形式:2.复数的几何形式:3.复数的向量形式:xyobaZ(a,b)z=a+bi3、复数的绝对值(也叫做复数的模)实数的绝对值在几何中
表示什么? |a|表示实数a在数轴上所对应的点A到原点O的距离.复数的绝对值在几何中表示什么呢?即时练习4 求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i
(4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)5 5 -5a 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个?(2)另解:设z=x+yi(x,y∈R)xyO11–1–1所以,复数|z|=1所对应
的点在复平面上构成一个以(0,0)为圆心,1为半径的圆。 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个? 这些复数z对应的点在复平面上将构成怎样的图形?(2)满足|z|=1(z∈C)的z值有几个?例2(1)满足|z|=1(z∈R)的z值有几个? 复数|z-2|=1表示复数z=x+yi所对应的点(x,y)到点(2,0)的距离等于1,在复平面上构成一个以(2,0)为圆心,1为半径的圆。变式1:已知复数z满足|z-2|=1,
求|z-3-4i|的最小值和最大值。变式2:已知复数z对应点Z,求下列条件下动点Z(x,y)的轨迹。
(1)|z-i|+|z+i|=4
(2)|z-2|=|z+4|
复数z=a+bi的模|z|= ,从几何意义上理解,表示点Z(a,b)和原点间的距离;类比向量的模还可进一步引申:|z1-z2|表示复数z1和z2对应的点Z1和Z2之间的距离.
小结二知识点:思想方法:(1)类比思想(3)数形结合思想(2)转化思想1.复数的代数形式:2.复数的几何形式:3.复数的向量形式:本课总结4.复数模|z|:|z1-z2|表示复数z1和z2对应的点Z1和Z2之间的距离作业课本P106
A组 4.(1)(3);5.(2)
B组 1,3谢谢大家!
