3.2.1 复数代数形式的加、减运算及其几何意义 课件22张PPT
文档属性
| 名称 | 3.2.1 复数代数形式的加、减运算及其几何意义 课件22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 688.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 00:00:00 | ||
图片预览







文档简介
课件22张PPT。复习回顾:一、两个复数a+bi和c+di相等的充要条件是什么?
二、复数Z=a+bi什么时候为实数?虚数?纯虚数?复数Z的模为多少?
三、复数Z=a+bi在复平面内对应的点的坐标为?
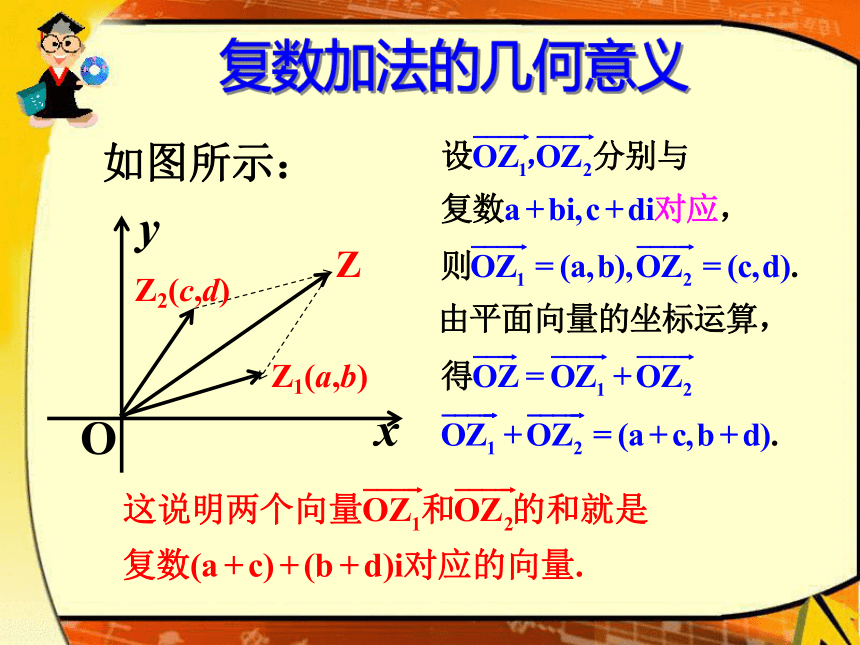
我们规定,复数的加法法则如下:很明显,两个复数的和仍然是一个确定的复数.设z1=a+bi, z2=c+di 是任意两个复数,那么 (a+bi)+(c+di)=(a+c)+(b+d)i.即:两个复数相加就是
实部与实部,虚部与虚部分别相加.复数的加法满足交换律、结合律如图所示:复数加法的几何意义(a+bi)-(c+di)=(a-c)+(b-d)i.复数的减法就是加法的逆运算.复数的减法法则:
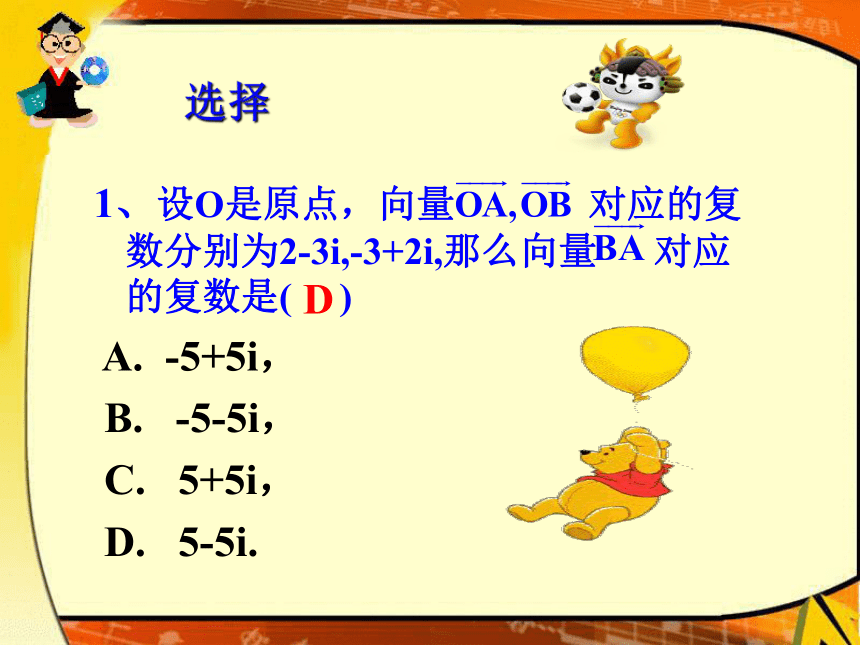
实部与实部,虚部与虚部分别相减.由此可见,两个复数的差是一个确定的复数.复数减法的几何意义解:计算 i+2i2+3i3+…+2004i2004D选择2、设z1=3-4i,z2=-2+3i,则z1+z2在复平面内对应的点位于( )
A. 第一象限,
B. 第二象限,
C. 第三象限,
D. 第四象限. D 我们规定,复数的乘法法则如下:设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积 复数的乘法与多项式的乘法是类似的,只要把结果中i2换成-1,把实部与虚部分别合并即可。计算 (1-2i)(3+4i)(-2+i)解: 原式=(11-2i)(-2+i)
=-20+15i.我们用乘法公式来进行计算.我们把这两个复数3+4i,3-4i称为共轭复数.注意本例 (1) 3+4i 与 3-4i 两复数的特点.一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )复数z=a+bi的共轭复数记作动动脑关于X轴对称实数除法法则:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后再化简.用上面的方法把分母“实数化”.(2007年广东卷)若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b为实数),则b=( )解析:(1+bi)(2+i)=(2-b)+(2b+1)i,故2-b=0,D随堂练习 D 答案:B.课时小结一、复数的加减法
二、复数的乘除法
三、共轭复数和分母“实数化”课后作业白皮125
二、复数Z=a+bi什么时候为实数?虚数?纯虚数?复数Z的模为多少?
三、复数Z=a+bi在复平面内对应的点的坐标为?
我们规定,复数的加法法则如下:很明显,两个复数的和仍然是一个确定的复数.设z1=a+bi, z2=c+di 是任意两个复数,那么 (a+bi)+(c+di)=(a+c)+(b+d)i.即:两个复数相加就是
实部与实部,虚部与虚部分别相加.复数的加法满足交换律、结合律如图所示:复数加法的几何意义(a+bi)-(c+di)=(a-c)+(b-d)i.复数的减法就是加法的逆运算.复数的减法法则:
实部与实部,虚部与虚部分别相减.由此可见,两个复数的差是一个确定的复数.复数减法的几何意义解:计算 i+2i2+3i3+…+2004i2004D选择2、设z1=3-4i,z2=-2+3i,则z1+z2在复平面内对应的点位于( )
A. 第一象限,
B. 第二象限,
C. 第三象限,
D. 第四象限. D 我们规定,复数的乘法法则如下:设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积 复数的乘法与多项式的乘法是类似的,只要把结果中i2换成-1,把实部与虚部分别合并即可。计算 (1-2i)(3+4i)(-2+i)解: 原式=(11-2i)(-2+i)
=-20+15i.我们用乘法公式来进行计算.我们把这两个复数3+4i,3-4i称为共轭复数.注意本例 (1) 3+4i 与 3-4i 两复数的特点.一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )复数z=a+bi的共轭复数记作动动脑关于X轴对称实数除法法则:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后再化简.用上面的方法把分母“实数化”.(2007年广东卷)若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b为实数),则b=( )解析:(1+bi)(2+i)=(2-b)+(2b+1)i,故2-b=0,D随堂练习 D 答案:B.课时小结一、复数的加减法
二、复数的乘除法
三、共轭复数和分母“实数化”课后作业白皮125
