3.2.1 复数代数形式的加、减运算及其几何意义课件20张PPT
文档属性
| 名称 | 3.2.1 复数代数形式的加、减运算及其几何意义课件20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 319.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 00:00:00 | ||
图片预览







文档简介
课件20张PPT。人教版A高中数学选修2-2复数代数形式的加减运算及其几何意义一、复习引入二、讲授新课1、复数的加法(1)设 ,规定(2)复数的加法运算满足加法的交换律、结合律,即对任意实数 有(3)抢答23i5-4i-2-i2、复数的减法(1)设 ,规定请你用一句话概括复数的加减法则。两个复数相加(减)就是:实部与实部,虚部与虚部分别相加减。(2)抢答3i-7+8i-4+10i-8+13i 思考:
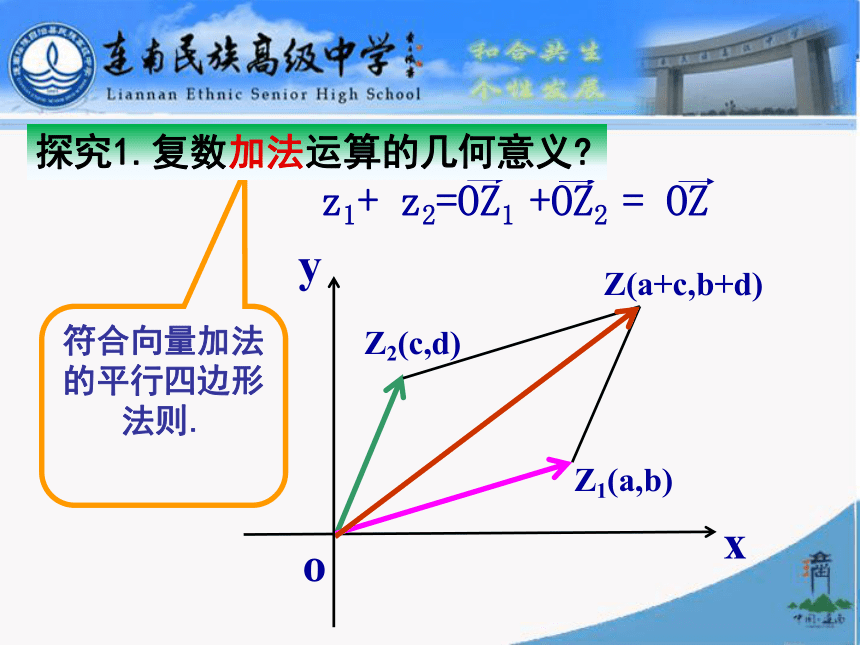
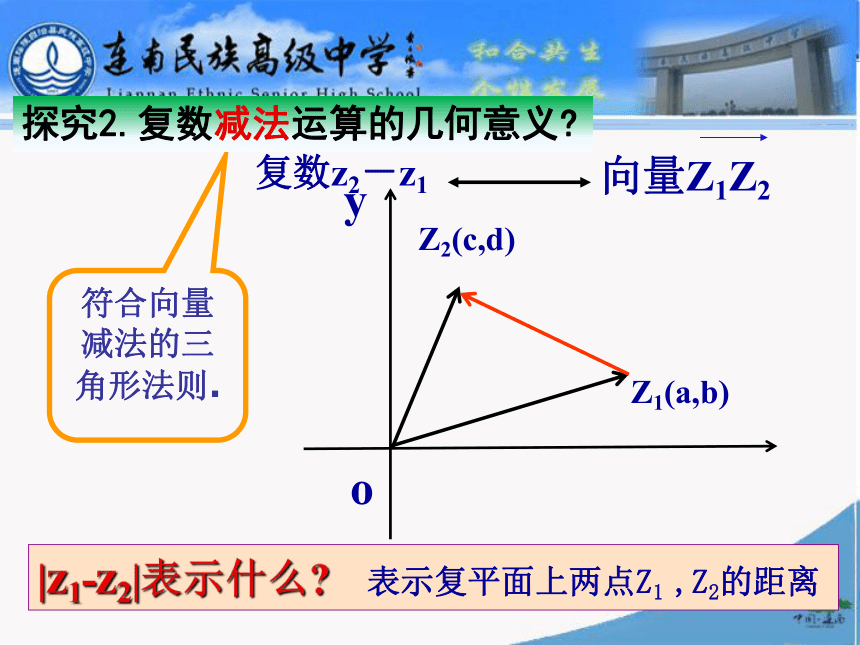
我们知道,两个向量的和满足平行四边形法则, 复数可以用平面上的向量表示,那么复数的加法与向量的加法是否具有一致性呢?如何用数形结合思想解析复数加法法则?三、探究活动xyZ1(a,b)Z2(c,d)符合向量加法的平行四边形法则.探究1.复数加法运算的几何意义?Z(a+c,b+d)ooyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.探究2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离例1 .复平面内点A、B分别对应复数 ZA=2-3i 和 ZB=-3+2i ,则向量 对应的复数是_________。5 - 5i四、典例分析结论1:复平面内点A、B分别对应复数 ZA 和 ZB ,则向量 对应的复数是__________.例2 .复平面内点A、B对应的复数分别为ZA=3+2i 和 ZB= -2+4i,则A、B间的距离是____变式1:复平面内点A、B对应的复数分别为 ZA=6+i 和 ZB= 2-2i,则A、B间的距离是___结论2:复平面内点A、B对应的复数分别为 ZA、ZB,则A、B间的距离是_____________.5例3.根据复数的几何意义,满足条件
的复数Z在复平面上对应的点的轨迹是
_____________________________________以(1,1)为圆心,半径为1的圆变式2: 满足条件 的复数Z在复平面上对应的点的轨迹是
______________________________________以(2,3)为圆心,半径为2的圆思考:根据例3及变式,你能归纳推导出一个
更一般的结论吗?结论3:满足条件 的复数z在复平面上对应的点的轨迹是
_____________________________________以(a,b)为圆心,半径为r的圆五、达标训练ADBDAD1.类比思想:
(代数角度)与实数之间的类比:复数的加减运算遵循实数运算的运算律和运算顺序;
(几何意义)与向量的概念、运算之间的类比。
2.数形结合:利用复数的几何意义解决距离、轨迹等的问题。六、总结提升七、布置作业教材P112 A组1,3再 见
我们知道,两个向量的和满足平行四边形法则, 复数可以用平面上的向量表示,那么复数的加法与向量的加法是否具有一致性呢?如何用数形结合思想解析复数加法法则?三、探究活动xyZ1(a,b)Z2(c,d)符合向量加法的平行四边形法则.探究1.复数加法运算的几何意义?Z(a+c,b+d)ooyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.探究2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离例1 .复平面内点A、B分别对应复数 ZA=2-3i 和 ZB=-3+2i ,则向量 对应的复数是_________。5 - 5i四、典例分析结论1:复平面内点A、B分别对应复数 ZA 和 ZB ,则向量 对应的复数是__________.例2 .复平面内点A、B对应的复数分别为ZA=3+2i 和 ZB= -2+4i,则A、B间的距离是____变式1:复平面内点A、B对应的复数分别为 ZA=6+i 和 ZB= 2-2i,则A、B间的距离是___结论2:复平面内点A、B对应的复数分别为 ZA、ZB,则A、B间的距离是_____________.5例3.根据复数的几何意义,满足条件
的复数Z在复平面上对应的点的轨迹是
_____________________________________以(1,1)为圆心,半径为1的圆变式2: 满足条件 的复数Z在复平面上对应的点的轨迹是
______________________________________以(2,3)为圆心,半径为2的圆思考:根据例3及变式,你能归纳推导出一个
更一般的结论吗?结论3:满足条件 的复数z在复平面上对应的点的轨迹是
_____________________________________以(a,b)为圆心,半径为r的圆五、达标训练ADBDAD1.类比思想:
(代数角度)与实数之间的类比:复数的加减运算遵循实数运算的运算律和运算顺序;
(几何意义)与向量的概念、运算之间的类比。
2.数形结合:利用复数的几何意义解决距离、轨迹等的问题。六、总结提升七、布置作业教材P112 A组1,3再 见
