3.2.2 复数代数形式的乘除运算 课件18张PPT
文档属性
| 名称 | 3.2.2 复数代数形式的乘除运算 课件18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 636.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 11:33:33 | ||
图片预览






文档简介
课件18张PPT。3.2.2 复数代数形式
的乘除运算 【学习目标】
1.理解并掌握复数代数形式的乘法与除法运算法则,理解除法是乘法运算的逆运算.
2.理解并掌握复数的乘法实质就是多项式展开,除法运算实质是分母实数化类问题.
【重点难点】
重点:复数的乘除运算法则及其应用.难点:复数的代数形式的化简已知两复数z1=a+bi,z2=c+di (a,b,c,d∈R)(a+bi)±(c+di) =________________.1.加法、减法的运算法则2.加法运算律:对任意z1,z2,z3∈Cz1+z2=(z1+z2)+z3=交换律:结合律:(a±c)+(b±d)i3.-1z2+z1,z1+(z2+z3) 1(3) 计算 (1+2i)(3-4i)(-2-i).阅读课本p109---110例2,例3
模仿例题完成课本p111练习1(3),2(1),(2).2(1)计算(2)计算【总结提升】
(1)实数集中的乘法公式在复数集中仍然成立;
(2)复数的混合运算也是先乘方,再乘除,最后加减,有括号应先处理括号里面的.探究点3 共轭复数的定义 一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
虚部不等于0的两个共轭复数也叫做共轭虚数.
实数的共轭复数是它本身.思考:若z1,z2是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
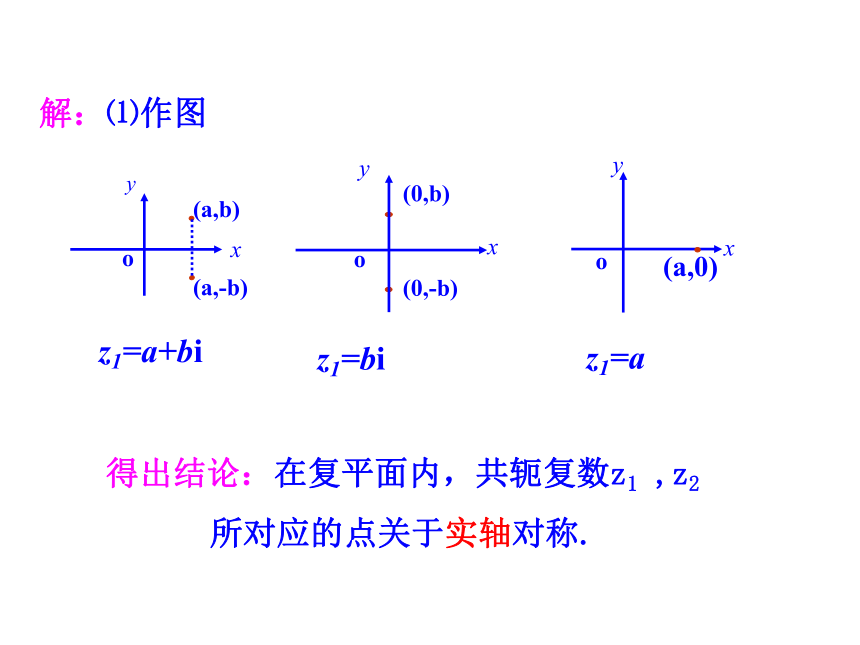
(2) z1·z2是一个怎样的数?解:⑴作图得出结论:在复平面内,共轭复数z1 ,z2 所对应的点关于实轴对称.⑵令z1=a+bi,则z2=a-bi
则z1·z2=(a+bi)(a-bi)
=a2-abi+abi-b2i2
=a2+b2
结论:任意两个互为共轭复数的乘积是一个实数.有理化因式使得分母探究点4 复数除法的法则
分子分母都乘以分母的共轭复数类似于根式的除法的分母有理化(分母实数化)(c+di≠0)结果化简成代数形式有理化因式分母的共轭复数使得分母实数化 阅读课本p111例4,(1分钟)
模仿例题完成课本p111练习3(1),(3),计算(3)先写成分式形式然后分母实数化,分子分母同时乘以分母的共轭复数结果化简成代数形式课本p111例4 阅读课本p111例4,
模仿例题完成课本p111练习3(1),(3),计算(3)四.能力提升:CC五.高考速递2.3.课后思考1.复数相乘类似于多项式相乘,只要在所得的结果中把i2换成-1,并且把实部和虚部分别合并.
2.实数系中的乘法公式在复数系中仍然成立.
3.当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
虚部不等于0的两个共轭复数也叫做共轭虚数.
实数的共轭复数是它本身.
4.复数代数形式的除法实质:分母实数化.课后作业:
《学案》p76页的例1,p77页,变式训练,A级1-8,10,B级1--3
的乘除运算 【学习目标】
1.理解并掌握复数代数形式的乘法与除法运算法则,理解除法是乘法运算的逆运算.
2.理解并掌握复数的乘法实质就是多项式展开,除法运算实质是分母实数化类问题.
【重点难点】
重点:复数的乘除运算法则及其应用.难点:复数的代数形式的化简已知两复数z1=a+bi,z2=c+di (a,b,c,d∈R)(a+bi)±(c+di) =________________.1.加法、减法的运算法则2.加法运算律:对任意z1,z2,z3∈Cz1+z2=(z1+z2)+z3=交换律:结合律:(a±c)+(b±d)i3.-1z2+z1,z1+(z2+z3) 1(3) 计算 (1+2i)(3-4i)(-2-i).阅读课本p109---110例2,例3
模仿例题完成课本p111练习1(3),2(1),(2).2(1)计算(2)计算【总结提升】
(1)实数集中的乘法公式在复数集中仍然成立;
(2)复数的混合运算也是先乘方,再乘除,最后加减,有括号应先处理括号里面的.探究点3 共轭复数的定义 一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
虚部不等于0的两个共轭复数也叫做共轭虚数.
实数的共轭复数是它本身.思考:若z1,z2是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
(2) z1·z2是一个怎样的数?解:⑴作图得出结论:在复平面内,共轭复数z1 ,z2 所对应的点关于实轴对称.⑵令z1=a+bi,则z2=a-bi
则z1·z2=(a+bi)(a-bi)
=a2-abi+abi-b2i2
=a2+b2
结论:任意两个互为共轭复数的乘积是一个实数.有理化因式使得分母探究点4 复数除法的法则
分子分母都乘以分母的共轭复数类似于根式的除法的分母有理化(分母实数化)(c+di≠0)结果化简成代数形式有理化因式分母的共轭复数使得分母实数化 阅读课本p111例4,(1分钟)
模仿例题完成课本p111练习3(1),(3),计算(3)先写成分式形式然后分母实数化,分子分母同时乘以分母的共轭复数结果化简成代数形式课本p111例4 阅读课本p111例4,
模仿例题完成课本p111练习3(1),(3),计算(3)四.能力提升:CC五.高考速递2.3.课后思考1.复数相乘类似于多项式相乘,只要在所得的结果中把i2换成-1,并且把实部和虚部分别合并.
2.实数系中的乘法公式在复数系中仍然成立.
3.当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
虚部不等于0的两个共轭复数也叫做共轭虚数.
实数的共轭复数是它本身.
4.复数代数形式的除法实质:分母实数化.课后作业:
《学案》p76页的例1,p77页,变式训练,A级1-8,10,B级1--3
