【A典演练】第2课时 第一章 第一节 探索勾股定理(2)习题 课件
文档属性
| 名称 | 【A典演练】第2课时 第一章 第一节 探索勾股定理(2)习题 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 696.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 10:51:44 | ||
图片预览


文档简介
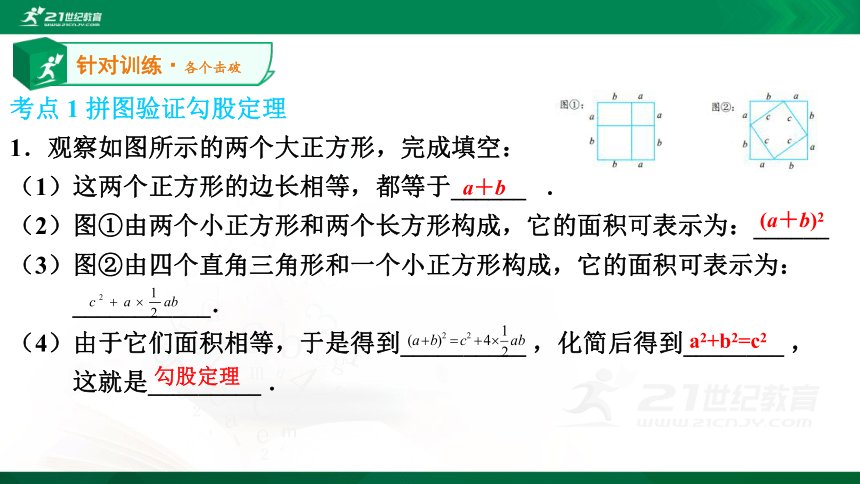
课件8张PPT。 第一单元 勾股定理第2课时 探索勾股定理(2)北师大版 九年级上册考点 1 拼图验证勾股定理
1.观察如图所示的两个大正方形,完成填空:
(1)这两个正方形的边长相等,都等于______ .
(2)图①由两个小正方形和两个长方形构成,它的面积可表示为:______
(3)图②由四个直角三角形和一个小正方形构成,它的面积可表示为:
___________.
(4)由于它们面积相等,于是得到__________ ,化简后得到________ ,
这就是_________ . 针对训练·各个击破a+b(a+b)2 a2+b2=c2勾股定理考点 2 勾股定理的实际应用
2.要从电线杆离地面 15 m 处向地面拉一条 17 m 长的电缆,则地面固定点
A到电线杆底部 B 的距离为( )
A.8 m B.15 m C.17 m D.25 m
3.“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个
大正方形,如图所示.若直角三角形的两条直角边的长分别是 5 和 3,
则小正方形的面积是( )
A.4 B.6 C.2 D.1
针对训练·各个击破AA考点 2 勾股定理的实际应用
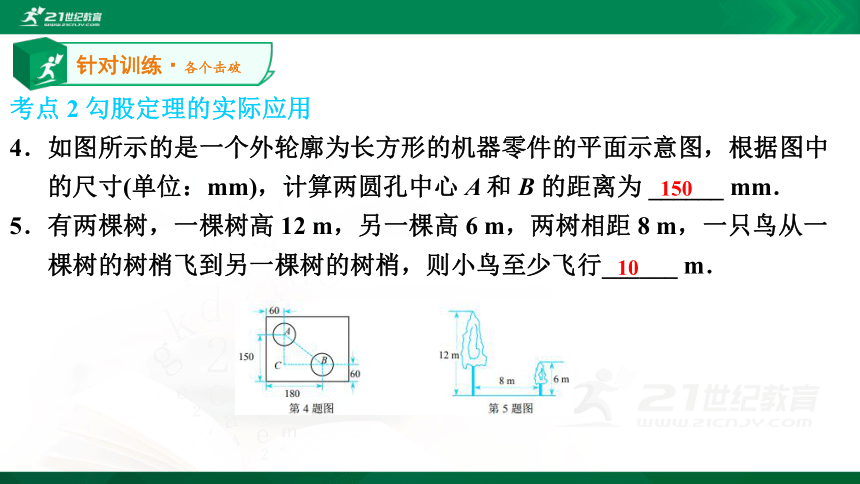
4.如图所示的是一个外轮廓为长方形的机器零件的平面示意图,根据图中
的尺寸(单位:mm),计算两圆孔中心 A 和 B 的距离为 ______ mm.
5.有两棵树,一棵树高 12 m,另一棵高 6 m,两树相距 8 m,一只鸟从一
棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行______ m.针对训练·各个击破150106.伽菲尔德(Garfield ,1881 年任美国第 20 届总统)利用下图证明了勾股定
理(1876 年 4 月 1 日,发表在《新英格兰教育日志》上),现请你尝试该证
明过程.
【答案】一方面,梯形 ABDE 的面积为
另一方面,梯形 ABDE 可分成三个直角三角形,
其面积又可以表示成
所以,
即 a2+b2=c2.
巩固提升·融会贯通7.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积
法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或
图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股
定理的过程:将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°.
求证:a2+b2=c2 .
证明:连接 DB,过点 D 作 BC 边上的高 DF,则 DF=EC=b-a.
∵S四边形 ADCB=S△ACD+S△ABC=
又∵S四边形 ADCB=S△ADB+S△DCB=
∴a2+b2=c2.
巩固提升·融会贯通 请参照上述证法,利用图②完成下面的证明.将两个全等的直角三角形按
图②所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
【答案】连接 BD,过点 B 作 DE 边上的高 BF,则 BF=b-a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE
∴a2+b2=c2.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.观察如图所示的两个大正方形,完成填空:
(1)这两个正方形的边长相等,都等于______ .
(2)图①由两个小正方形和两个长方形构成,它的面积可表示为:______
(3)图②由四个直角三角形和一个小正方形构成,它的面积可表示为:
___________.
(4)由于它们面积相等,于是得到__________ ,化简后得到________ ,
这就是_________ . 针对训练·各个击破a+b(a+b)2 a2+b2=c2勾股定理考点 2 勾股定理的实际应用
2.要从电线杆离地面 15 m 处向地面拉一条 17 m 长的电缆,则地面固定点
A到电线杆底部 B 的距离为( )
A.8 m B.15 m C.17 m D.25 m
3.“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个
大正方形,如图所示.若直角三角形的两条直角边的长分别是 5 和 3,
则小正方形的面积是( )
A.4 B.6 C.2 D.1
针对训练·各个击破AA考点 2 勾股定理的实际应用
4.如图所示的是一个外轮廓为长方形的机器零件的平面示意图,根据图中
的尺寸(单位:mm),计算两圆孔中心 A 和 B 的距离为 ______ mm.
5.有两棵树,一棵树高 12 m,另一棵高 6 m,两树相距 8 m,一只鸟从一
棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行______ m.针对训练·各个击破150106.伽菲尔德(Garfield ,1881 年任美国第 20 届总统)利用下图证明了勾股定
理(1876 年 4 月 1 日,发表在《新英格兰教育日志》上),现请你尝试该证
明过程.
【答案】一方面,梯形 ABDE 的面积为
另一方面,梯形 ABDE 可分成三个直角三角形,
其面积又可以表示成
所以,
即 a2+b2=c2.
巩固提升·融会贯通7.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积
法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或
图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股
定理的过程:将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°.
求证:a2+b2=c2 .
证明:连接 DB,过点 D 作 BC 边上的高 DF,则 DF=EC=b-a.
∵S四边形 ADCB=S△ACD+S△ABC=
又∵S四边形 ADCB=S△ADB+S△DCB=
∴a2+b2=c2.
巩固提升·融会贯通 请参照上述证法,利用图②完成下面的证明.将两个全等的直角三角形按
图②所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
【答案】连接 BD,过点 B 作 DE 边上的高 BF,则 BF=b-a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE
∴a2+b2=c2.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
