人教版必修二1.1.1多面体的结构特征课件(19张)
文档属性
| 名称 | 人教版必修二1.1.1多面体的结构特征课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 00:00:00 | ||
图片预览





文档简介
课件19张PPT。第一章 空间几何体1.1 空间几何体的结构第1课时 多面体的结构特征1.理解多面体的概念.
2.理解棱柱、棱锥、棱台的
相关概念.(重点)
3.掌握棱柱、棱锥、棱台的
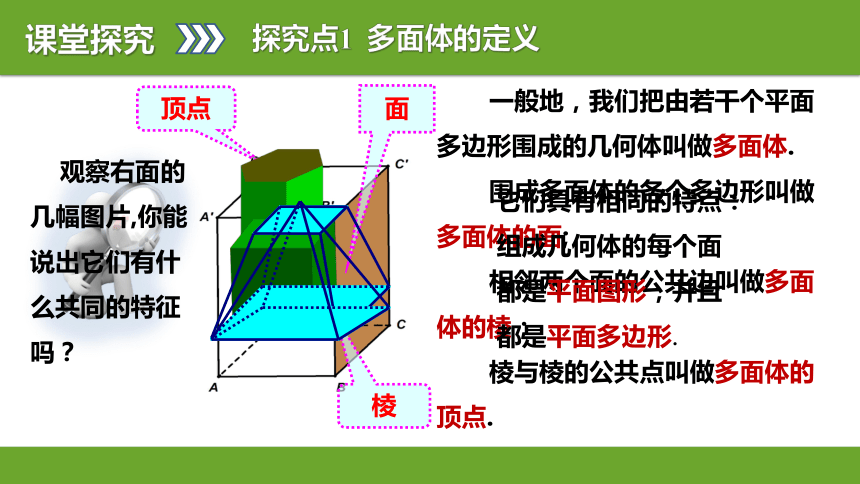
结构特征.(难点)学习目标 观察右面的几幅图片,你能说出它们有什么共同的特征吗?课堂探究探究点1 多面体的定义 一般地,我们把由若干个平面
多边形围成的几何体叫做多面体.
围成多面体的各个多边形叫做
多面体的面;
相邻两个面的公共边叫做多面
体的棱;
棱与棱的公共点叫做多面体的
顶点.面棱顶点课堂探究探究点1 多面体的定义 观察右面的几幅图片,你能说出它们有什么共同的特征吗?它们具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形.各小组,观察你们手中的模型,
说说它是棱柱、棱锥、还是棱台?有怎样的结构特征?
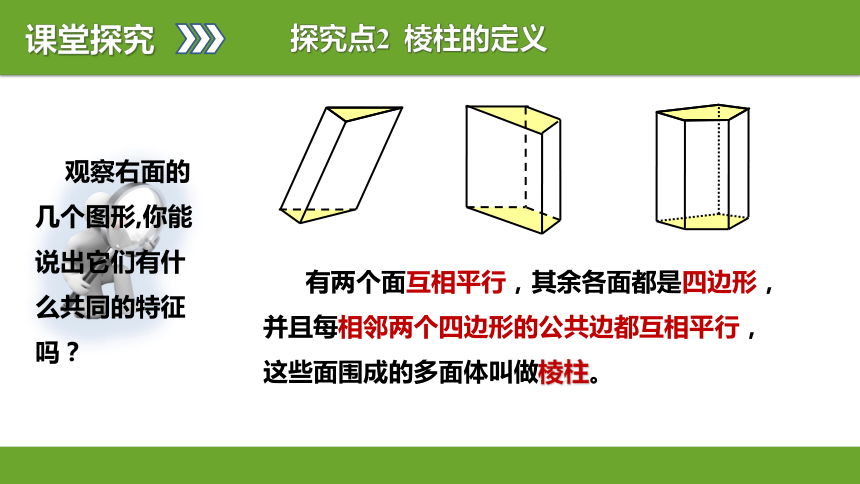
请把你们观察到的结构特征,写在学案上。课堂探究课堂探究探究点2 棱柱的定义 有两个面互相平行,其余各面都是四边形,
并且每相邻两个四边形的公共边都互相平行,
这些面围成的多面体叫做棱柱。 课堂探究探究点3 棱柱的结构特征两个互相平行的面叫做棱柱的底面或底;
其余各面叫做棱柱的侧面。两个面的公共边叫做棱柱的棱;
两个侧面的公共边叫做棱柱的侧棱。底面多边形与侧面的公共顶点叫做棱柱的顶点。 棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……。底面底面侧面侧棱顶点棱柱的表示方法:ABCDEF-A’B’C’D’E’F’。课堂探究探究点4 棱锥的定义 有一个面是多边形,
其余各面都是有一个公共顶点的三角形,
由这些面围成的多面体叫做棱锥。 课堂探究探究点5 棱锥的结构特征这个多边形面叫做棱锥的底面或底;
有公共顶点的三角形面叫做棱锥的侧面。相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点。 棱锥的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱锥、四棱锥、五棱锥……。侧面侧棱顶点底面棱锥的表示方法:S—ABCDE。课堂探究探究点6 棱台的定义用一个平行于
棱锥底面的平
面去截棱锥,
底面与截面之
间的部分,
这样的多面体叫做棱台.四棱锥平行于棱锥底面的平面课堂探究探究点7 棱台的结构特征原棱锥的底面和截面叫做棱台的下底面和上底面;
原棱锥的侧面剩下的部分叫做棱台的侧面。相邻侧面的公共边叫做棱台的侧棱;原棱锥底面的顶点和截面与侧棱的交点叫做
棱台的顶点。由三棱锥、四棱锥、五棱锥……截得的棱台
分别叫做三棱台、四棱台、五棱台……。侧面侧棱下底面上底面棱台的表示方法:ABCD-A’B’C’D’。ABCDA’B’C ’D’典例精讲例1 下列几何体中是棱柱的有 ( )A.1个 B.2个 C.3个 D.4个C例2 判断下列几何体是不是棱台.典例精讲【解析】都不是棱台.
左图的侧棱延长线不交于一点;
右图不适用平行于棱锥底面的平面截得的。变式练习 判断下列几何体是不是棱台.[解析] A项中的几何体是棱柱;B项中的几何体是棱锥;D项中的几何体的棱AA′,BB′,CC′,DD′没有交于一点,则D项中的几何体不是棱台;很明显C项中的几何体是棱台.课堂检测C1.棱台不一定具有的性质是 ( )
A.两底面相似
B.侧面都是梯形
C.侧棱都相等
D.侧棱延长后都交于一点课堂检测2.下列结论正确的是 ( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.一个棱柱至少有五个面,六个顶点、九条棱
C.一个棱锥至少有四个面、四个顶点、四条棱
D.棱锥截去一个小棱锥后剩余部分是棱台
【解析】由棱柱的定义知,A不正确;棱数最少的三棱锥有四个面、四个顶点、六条棱,C不正确;对于棱锥,用不平行于底面的平面截去一个小棱锥后,剩余部分不是棱台,D不正确;B正确.B3.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_________. 【解析】有10个顶点的棱柱为五棱柱,而五棱柱有5条侧棱,故每条侧棱长为12 cm.课堂检测12cm课堂小结多面体分类棱
柱棱
锥棱
台判断一个几何体是否为棱台:
①各侧棱的延长线是否相交于一点;
②截面是否平行于原棱锥的底面.棱柱的结构特征:
①有两个面互相平行;
②其余各面是四边形;
③每相邻两个四边形的公共边都互相平行.判断一个几何体是否为棱锥:
各侧面是否是有一个公共顶点的三角形.谢谢观看!第一章 空间几何体
2.理解棱柱、棱锥、棱台的
相关概念.(重点)
3.掌握棱柱、棱锥、棱台的
结构特征.(难点)学习目标 观察右面的几幅图片,你能说出它们有什么共同的特征吗?课堂探究探究点1 多面体的定义 一般地,我们把由若干个平面
多边形围成的几何体叫做多面体.
围成多面体的各个多边形叫做
多面体的面;
相邻两个面的公共边叫做多面
体的棱;
棱与棱的公共点叫做多面体的
顶点.面棱顶点课堂探究探究点1 多面体的定义 观察右面的几幅图片,你能说出它们有什么共同的特征吗?它们具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形.各小组,观察你们手中的模型,
说说它是棱柱、棱锥、还是棱台?有怎样的结构特征?
请把你们观察到的结构特征,写在学案上。课堂探究课堂探究探究点2 棱柱的定义 有两个面互相平行,其余各面都是四边形,
并且每相邻两个四边形的公共边都互相平行,
这些面围成的多面体叫做棱柱。 课堂探究探究点3 棱柱的结构特征两个互相平行的面叫做棱柱的底面或底;
其余各面叫做棱柱的侧面。两个面的公共边叫做棱柱的棱;
两个侧面的公共边叫做棱柱的侧棱。底面多边形与侧面的公共顶点叫做棱柱的顶点。 棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……。底面底面侧面侧棱顶点棱柱的表示方法:ABCDEF-A’B’C’D’E’F’。课堂探究探究点4 棱锥的定义 有一个面是多边形,
其余各面都是有一个公共顶点的三角形,
由这些面围成的多面体叫做棱锥。 课堂探究探究点5 棱锥的结构特征这个多边形面叫做棱锥的底面或底;
有公共顶点的三角形面叫做棱锥的侧面。相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点。 棱锥的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱锥、四棱锥、五棱锥……。侧面侧棱顶点底面棱锥的表示方法:S—ABCDE。课堂探究探究点6 棱台的定义用一个平行于
棱锥底面的平
面去截棱锥,
底面与截面之
间的部分,
这样的多面体叫做棱台.四棱锥平行于棱锥底面的平面课堂探究探究点7 棱台的结构特征原棱锥的底面和截面叫做棱台的下底面和上底面;
原棱锥的侧面剩下的部分叫做棱台的侧面。相邻侧面的公共边叫做棱台的侧棱;原棱锥底面的顶点和截面与侧棱的交点叫做
棱台的顶点。由三棱锥、四棱锥、五棱锥……截得的棱台
分别叫做三棱台、四棱台、五棱台……。侧面侧棱下底面上底面棱台的表示方法:ABCD-A’B’C’D’。ABCDA’B’C ’D’典例精讲例1 下列几何体中是棱柱的有 ( )A.1个 B.2个 C.3个 D.4个C例2 判断下列几何体是不是棱台.典例精讲【解析】都不是棱台.
左图的侧棱延长线不交于一点;
右图不适用平行于棱锥底面的平面截得的。变式练习 判断下列几何体是不是棱台.[解析] A项中的几何体是棱柱;B项中的几何体是棱锥;D项中的几何体的棱AA′,BB′,CC′,DD′没有交于一点,则D项中的几何体不是棱台;很明显C项中的几何体是棱台.课堂检测C1.棱台不一定具有的性质是 ( )
A.两底面相似
B.侧面都是梯形
C.侧棱都相等
D.侧棱延长后都交于一点课堂检测2.下列结论正确的是 ( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.一个棱柱至少有五个面,六个顶点、九条棱
C.一个棱锥至少有四个面、四个顶点、四条棱
D.棱锥截去一个小棱锥后剩余部分是棱台
【解析】由棱柱的定义知,A不正确;棱数最少的三棱锥有四个面、四个顶点、六条棱,C不正确;对于棱锥,用不平行于底面的平面截去一个小棱锥后,剩余部分不是棱台,D不正确;B正确.B3.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_________. 【解析】有10个顶点的棱柱为五棱柱,而五棱柱有5条侧棱,故每条侧棱长为12 cm.课堂检测12cm课堂小结多面体分类棱
柱棱
锥棱
台判断一个几何体是否为棱台:
①各侧棱的延长线是否相交于一点;
②截面是否平行于原棱锥的底面.棱柱的结构特征:
①有两个面互相平行;
②其余各面是四边形;
③每相邻两个四边形的公共边都互相平行.判断一个几何体是否为棱锥:
各侧面是否是有一个公共顶点的三角形.谢谢观看!第一章 空间几何体
