人教版必修二习题1、3 有关多面体的外接球问题课件(23张)
文档属性
| 名称 | 人教版必修二习题1、3 有关多面体的外接球问题课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 558.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-15 12:28:23 | ||
图片预览




文档简介
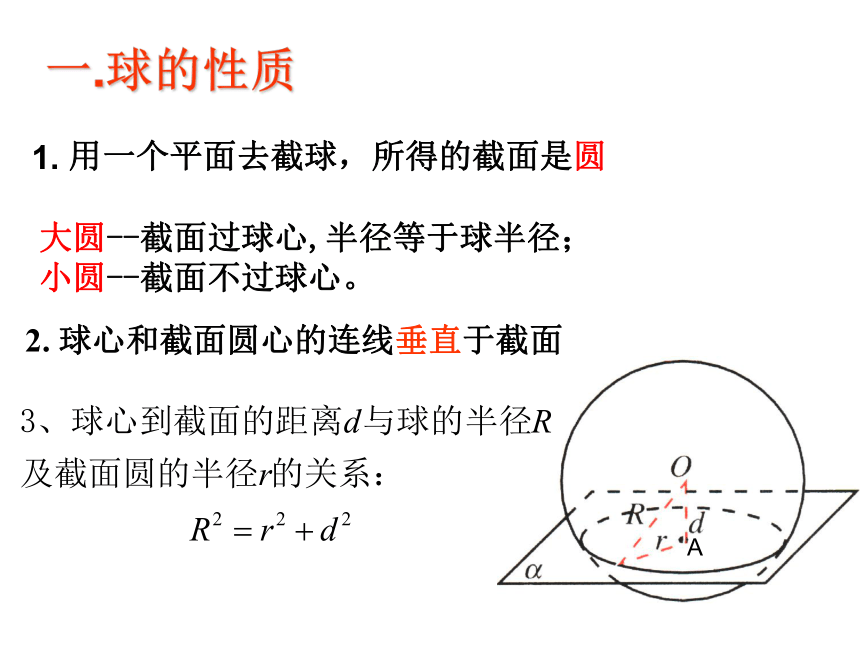
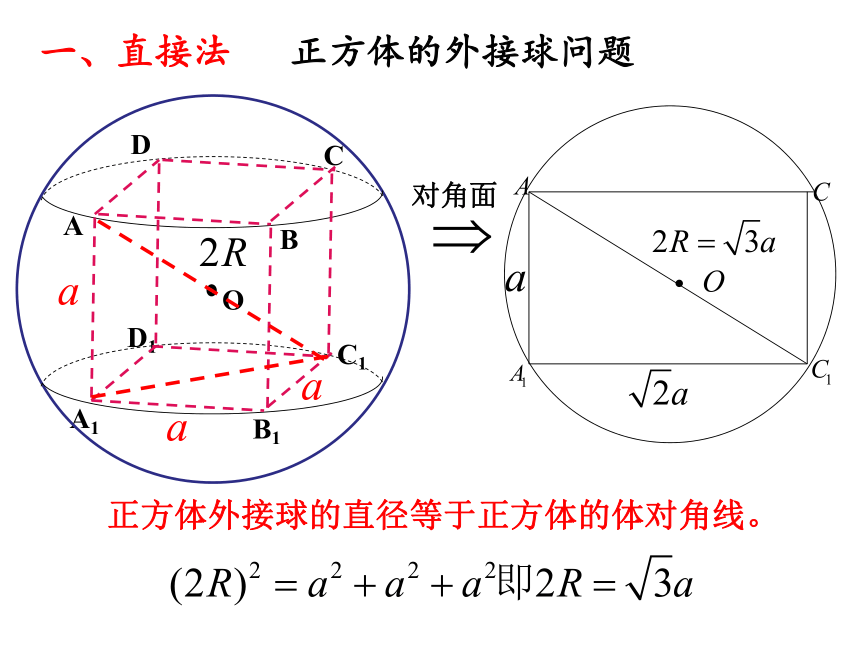
课件23张PPT。简单多面体的外接球问题一.球的性质 1. 用一个平面去截球,所得的截面是圆大圆--截面过球心,半径等于球半径;
小圆--截面不过球心。A2. 球心和截面圆心的连线垂直于截面
三. 多面体的外接球的定义定义:若一个多面体的各顶点都在一个球的球面上,则称这个球是这个多面体的外接球。 二.球体的体积与表面积简单多面体外接球的半径的求法方法一:直接法
方法二:补形法
方法三:构造直角三角形
方法四:确定球的球心法
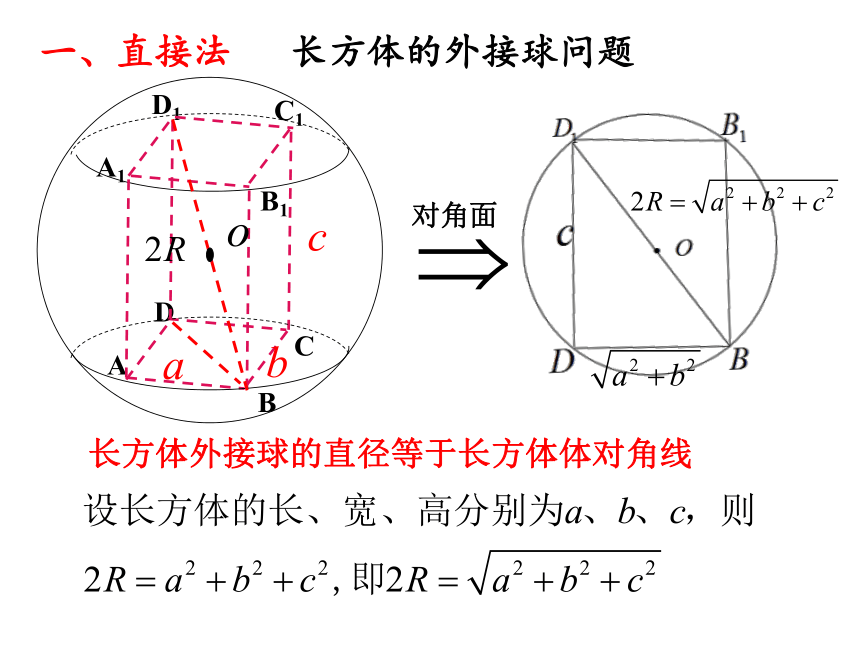
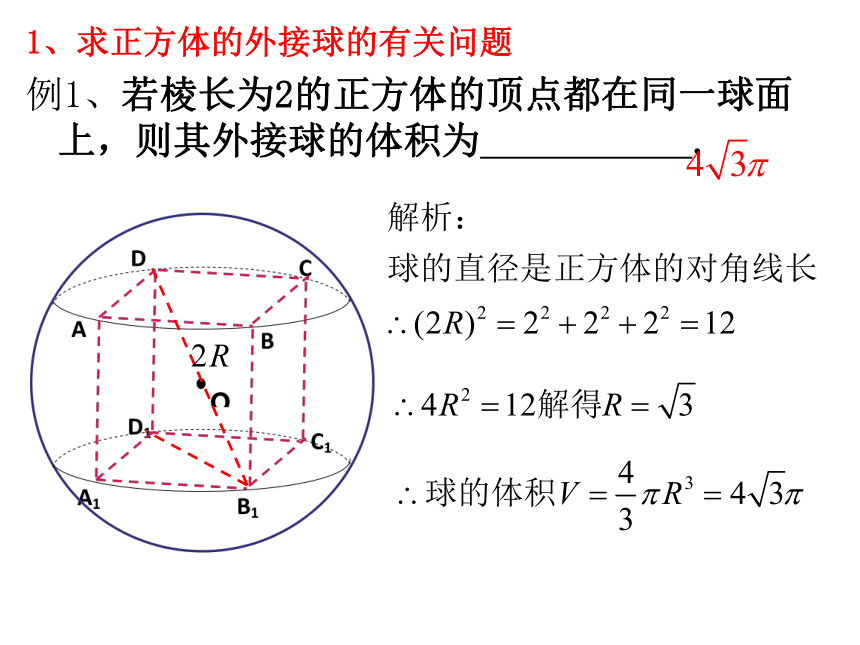
对角面正方体外接球的直径等于正方体的体对角线。正方体的外接球问题一、直接法对角面长方体外接球的直径等于长方体体对角线长方体的外接球问题一、直接法1、求正方体的外接球的有关问题
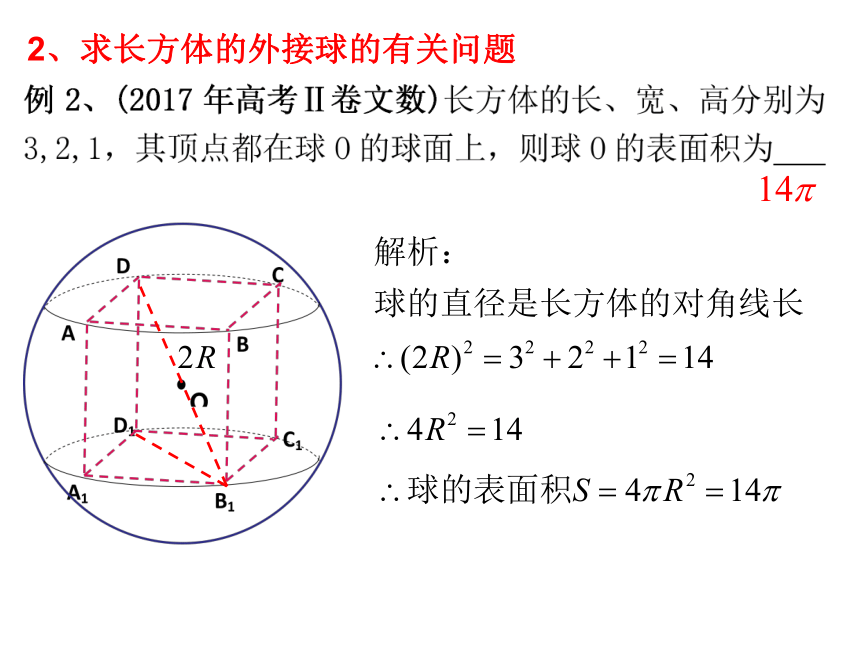
例1、若棱长为2的正方体的顶点都在同一球面上,则其外接球的体积为 .2、求长方体的外接球的有关问题方法一:直接法一、长方体和正方体的外接球的有关问题长方体或正方体的体对角线的长等于其外接球的直径二、补形法补形为长方体思考总结1: 什么样的三棱柱可直接补形成正方体或长方体?底面是直角三角形的直棱柱可补成正方体
或长方体二、补形法补形为正方体二、补形法二、补形法思考总结2: 什么样的棱锥可直接补形成正方体或长方体?求棱锥外接球半径常见的补形有:
1、正四面体常补成正方体;
2、三条侧棱两两垂直的三棱锥常补成正方体或长方体;
3、有一条侧棱垂直于底面且底面是直角三角形的三棱锥常补成正方体或长方体;
4、有一条侧棱垂直于底面且底面是距形的四棱锥可补成正方体或长方体。思考总结3:若多面体有一条侧棱垂直底面但底面不是直角三角形或矩形的棱锥和棱柱能不能直接补成正方体或长方体?那么怎样求其外接球的半径?方法三:构造直三角形方法三:构造直三角形课堂练习;1、直三棱柱的外接球问题球心在上下底面三角形外接圆心连线线段的中点。设球半径为R,球心到底面ABC的距离为d,ΔABC的外接圆半径为r.设直三棱柱高AA1=2a.2、有一条侧棱垂直底面的棱锥的外接球问题(以底面为三角形的三棱锥为例)设球半径为R,ΔABC的外接圆半径为r.设三棱锥的高SA=2a.简单多面体外接球的半径的求法方法一:直接法
方法二:补形法
方法三:构造直角三角形(勾股定理)
小结:
小圆--截面不过球心。A2. 球心和截面圆心的连线垂直于截面
三. 多面体的外接球的定义定义:若一个多面体的各顶点都在一个球的球面上,则称这个球是这个多面体的外接球。 二.球体的体积与表面积简单多面体外接球的半径的求法方法一:直接法
方法二:补形法
方法三:构造直角三角形
方法四:确定球的球心法
对角面正方体外接球的直径等于正方体的体对角线。正方体的外接球问题一、直接法对角面长方体外接球的直径等于长方体体对角线长方体的外接球问题一、直接法1、求正方体的外接球的有关问题
例1、若棱长为2的正方体的顶点都在同一球面上,则其外接球的体积为 .2、求长方体的外接球的有关问题方法一:直接法一、长方体和正方体的外接球的有关问题长方体或正方体的体对角线的长等于其外接球的直径二、补形法补形为长方体思考总结1: 什么样的三棱柱可直接补形成正方体或长方体?底面是直角三角形的直棱柱可补成正方体
或长方体二、补形法补形为正方体二、补形法二、补形法思考总结2: 什么样的棱锥可直接补形成正方体或长方体?求棱锥外接球半径常见的补形有:
1、正四面体常补成正方体;
2、三条侧棱两两垂直的三棱锥常补成正方体或长方体;
3、有一条侧棱垂直于底面且底面是直角三角形的三棱锥常补成正方体或长方体;
4、有一条侧棱垂直于底面且底面是距形的四棱锥可补成正方体或长方体。思考总结3:若多面体有一条侧棱垂直底面但底面不是直角三角形或矩形的棱锥和棱柱能不能直接补成正方体或长方体?那么怎样求其外接球的半径?方法三:构造直三角形方法三:构造直三角形课堂练习;1、直三棱柱的外接球问题球心在上下底面三角形外接圆心连线线段的中点。设球半径为R,球心到底面ABC的距离为d,ΔABC的外接圆半径为r.设直三棱柱高AA1=2a.2、有一条侧棱垂直底面的棱锥的外接球问题(以底面为三角形的三棱锥为例)设球半径为R,ΔABC的外接圆半径为r.设三棱锥的高SA=2a.简单多面体外接球的半径的求法方法一:直接法
方法二:补形法
方法三:构造直角三角形(勾股定理)
小结:
