6.4组合图形的面积 课件(24张ppt)
文档属性
| 名称 | 6.4组合图形的面积 课件(24张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 14:27:07 | ||
图片预览




文档简介
(共24张PPT)
优翼
第7课时 组合图形的面积
多边形的面积
6
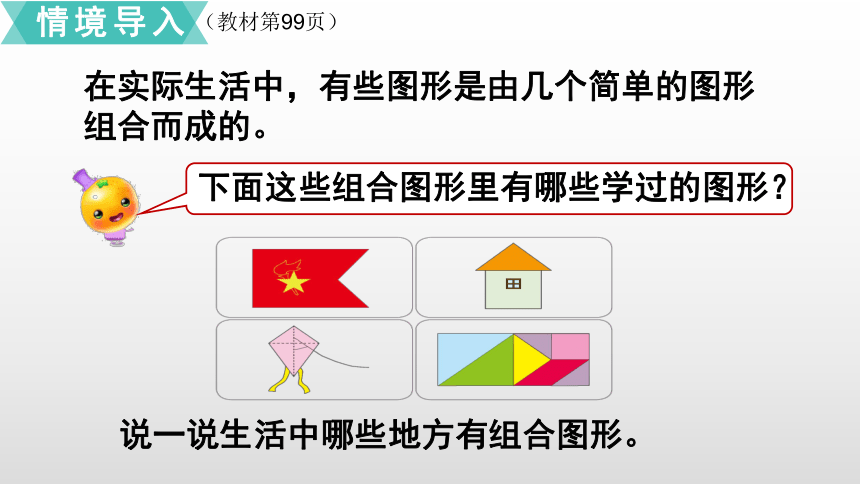
在实际生活中,有些图形是由几个简单的图形
组合而成的。
下面这些组合图形里有哪些学过的图形?
说一说生活中哪些地方有组合图形。
情境导入
(教材第99页)
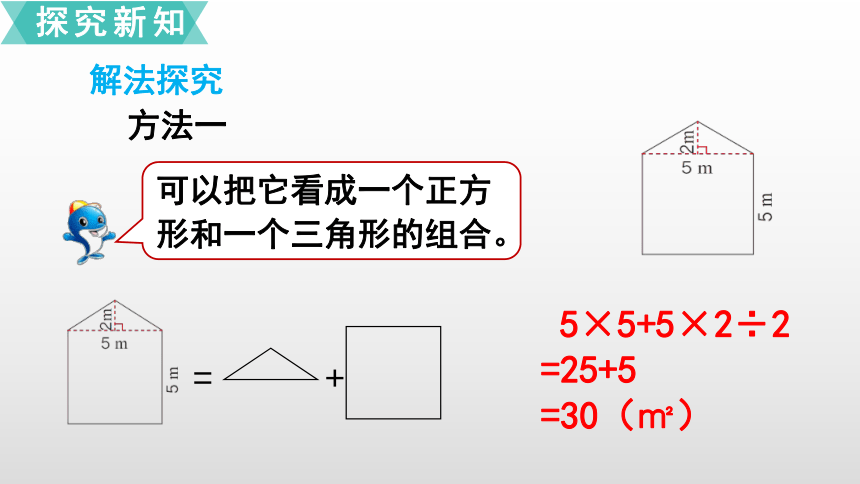
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
你能用自己的方法求出它的面积吗?
探究新知
(教材99页例4)
4
知识点:组合图形面积的计算
可以把它看成一个正方形和一个三角形的组合。
解法探究
方法一
5×5+5×2÷2
=25+5
=30(㎡)
=
+
探究新知
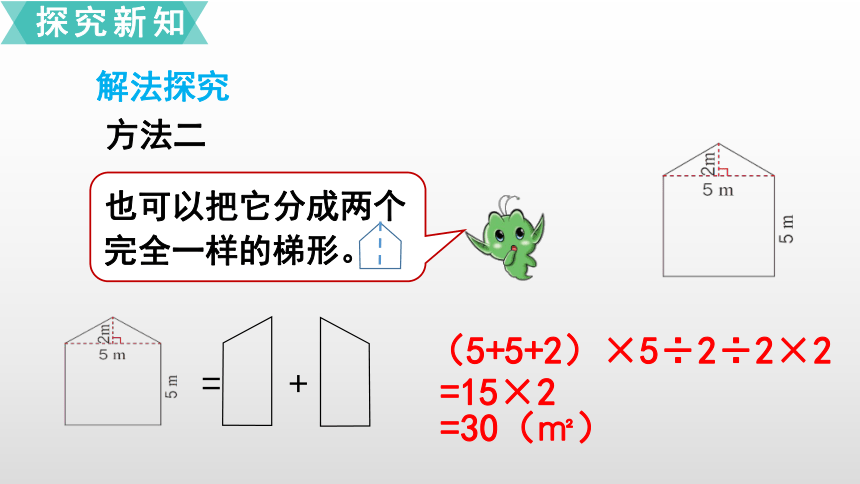
方法二
也可以把它分成两个完全一样的梯形。
=
+
=15×2
=30(㎡)
(5+5+2)×5÷2÷2×2
解法探究
探究新知
方法小结
计算组合图形面积的方法:
要根据已知条件对图形进行分解,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
刚才的题目,你还有其他解法吗?
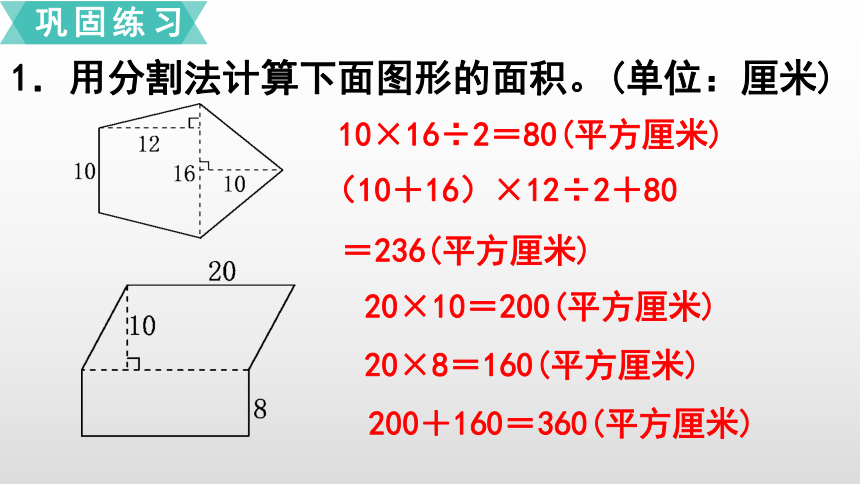
20×10=200(平方厘米)
20×8=160(平方厘米)
200+160=360(平方厘米)
巩固练习
10×16÷2=80(平方厘米)
(10+16)×12÷2+80
=236(平方厘米)
1.用分割法计算下面图形的面积。(单位:厘米)
2.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
巩固练习
(教材101页第4题)
(70+40)×30÷2-30×15
= 110×30÷2-450
= 3300÷2-450
= 1650-450
= 1200(m2)
答:草地的面积是1200m2
为什么不用分和拼的方法呢?
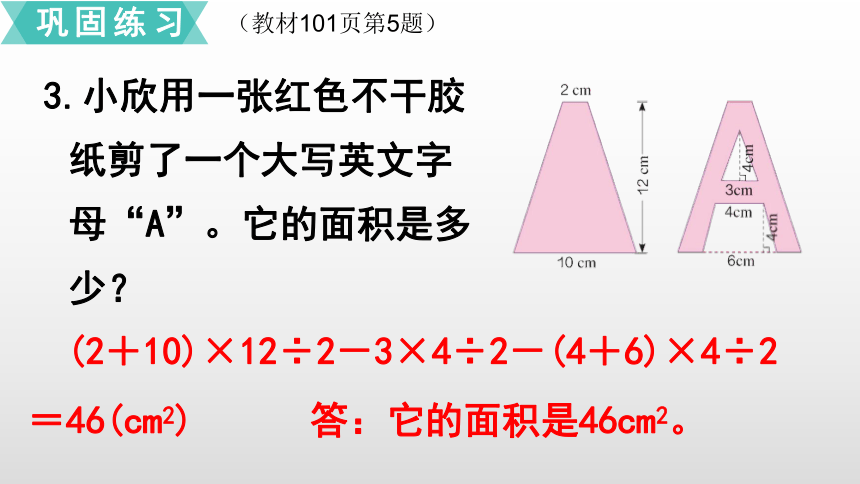
3.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2-3×4÷2-(4+6)×4÷2
=46(cm2) 答:它的面积是46cm2。
巩固练习
(教材101页第5题)
巩固练习
(教材101页第6题)
4.一个指示牌的形状是一个组合图形,求它的面积。
20×10 + 20×10÷2 = 300(cm2)
答:它的面积是300cm2 。
分析:长方形 + 三角形
1.从课后习题中选取;
2.完成练习册本课时的习题。
课外作业
优翼
第8课时 不规则图形的面积
多边形的面积
6
计算下面图形的面积。
4m
10m
10m
3m
4m
3m
5m
5×3+5×4=35(m2)
10×10 - 3×4÷2=94(m2)
复习导入
图中每个小方格的面积是1cm2 ,请你估计这片叶子的面积。
探究新知
5
(教材100页例5)
知识点1:方格纸中不规则图形面积的估算
知道小方格的面积,求叶子的面积。
阅读与理解
探究新知
先在方格纸上描出叶子的轮廓图。
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2—36cm2之间。
如果把不满一格的都按半格计算,这片叶子的面积大约27cm2。
分析与解答
探究新知
我是将叶子的图形近似转化成平行四边形……
S=ah
=5×6
=30(cm2)
你是怎样估的?
探究新知
不规则图形的面积可以转化为学过的图形来估算。
先通过数方格确定面积的范围,再……
回顾与反思
探究新知
估计不规则图形的面积:
借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
方法小结
1.有一块地近似平行四边形,底是43 m,高是20.1 m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1≈864(m2)
答:这块地的面积约是864m2。
巩固练习
(教材102页第7 题)
2.图中每个小方格的面积为1cm2,计算阴
影部分面积。
巩固练习
(教材102页第8 题)
三角形 + 梯形
5×4÷2 + (5+2)×4÷2
= 24(cm2)
近似转化成长方形
8×4 = 32(cm2)
阴影部分面积大约是 32cm2。
巩固练习
2.图中每个小方格的面积为1cm2,计算阴
影部分面积。
(教材102页第8 题)
3.图中每个小方格的面积为1m2,请你估
计这个池塘的面积。
S =ab
=12×8
=96(m2 )
这个池塘的面积大约是96m2。
巩固练习
(教材102页第9 题)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课外作业
优翼
第7课时 组合图形的面积
多边形的面积
6
在实际生活中,有些图形是由几个简单的图形
组合而成的。
下面这些组合图形里有哪些学过的图形?
说一说生活中哪些地方有组合图形。
情境导入
(教材第99页)
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
你能用自己的方法求出它的面积吗?
探究新知
(教材99页例4)
4
知识点:组合图形面积的计算
可以把它看成一个正方形和一个三角形的组合。
解法探究
方法一
5×5+5×2÷2
=25+5
=30(㎡)
=
+
探究新知
方法二
也可以把它分成两个完全一样的梯形。
=
+
=15×2
=30(㎡)
(5+5+2)×5÷2÷2×2
解法探究
探究新知
方法小结
计算组合图形面积的方法:
要根据已知条件对图形进行分解,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
刚才的题目,你还有其他解法吗?
20×10=200(平方厘米)
20×8=160(平方厘米)
200+160=360(平方厘米)
巩固练习
10×16÷2=80(平方厘米)
(10+16)×12÷2+80
=236(平方厘米)
1.用分割法计算下面图形的面积。(单位:厘米)
2.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
巩固练习
(教材101页第4题)
(70+40)×30÷2-30×15
= 110×30÷2-450
= 3300÷2-450
= 1650-450
= 1200(m2)
答:草地的面积是1200m2
为什么不用分和拼的方法呢?
3.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2-3×4÷2-(4+6)×4÷2
=46(cm2) 答:它的面积是46cm2。
巩固练习
(教材101页第5题)
巩固练习
(教材101页第6题)
4.一个指示牌的形状是一个组合图形,求它的面积。
20×10 + 20×10÷2 = 300(cm2)
答:它的面积是300cm2 。
分析:长方形 + 三角形
1.从课后习题中选取;
2.完成练习册本课时的习题。
课外作业
优翼
第8课时 不规则图形的面积
多边形的面积
6
计算下面图形的面积。
4m
10m
10m
3m
4m
3m
5m
5×3+5×4=35(m2)
10×10 - 3×4÷2=94(m2)
复习导入
图中每个小方格的面积是1cm2 ,请你估计这片叶子的面积。
探究新知
5
(教材100页例5)
知识点1:方格纸中不规则图形面积的估算
知道小方格的面积,求叶子的面积。
阅读与理解
探究新知
先在方格纸上描出叶子的轮廓图。
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2—36cm2之间。
如果把不满一格的都按半格计算,这片叶子的面积大约27cm2。
分析与解答
探究新知
我是将叶子的图形近似转化成平行四边形……
S=ah
=5×6
=30(cm2)
你是怎样估的?
探究新知
不规则图形的面积可以转化为学过的图形来估算。
先通过数方格确定面积的范围,再……
回顾与反思
探究新知
估计不规则图形的面积:
借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
方法小结
1.有一块地近似平行四边形,底是43 m,高是20.1 m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1≈864(m2)
答:这块地的面积约是864m2。
巩固练习
(教材102页第7 题)
2.图中每个小方格的面积为1cm2,计算阴
影部分面积。
巩固练习
(教材102页第8 题)
三角形 + 梯形
5×4÷2 + (5+2)×4÷2
= 24(cm2)
近似转化成长方形
8×4 = 32(cm2)
阴影部分面积大约是 32cm2。
巩固练习
2.图中每个小方格的面积为1cm2,计算阴
影部分面积。
(教材102页第8 题)
3.图中每个小方格的面积为1m2,请你估
计这个池塘的面积。
S =ab
=12×8
=96(m2 )
这个池塘的面积大约是96m2。
巩固练习
(教材102页第9 题)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课外作业
