1.1.2 导数的几何意义课件18张PPT
文档属性
| 名称 | 1.1.2 导数的几何意义课件18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 198.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:03:11 | ||
图片预览



文档简介
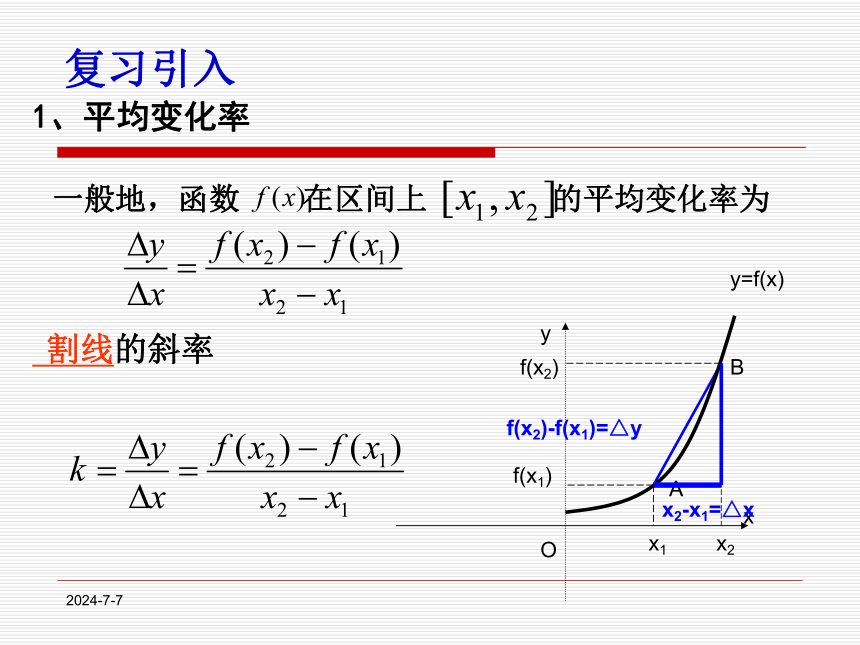
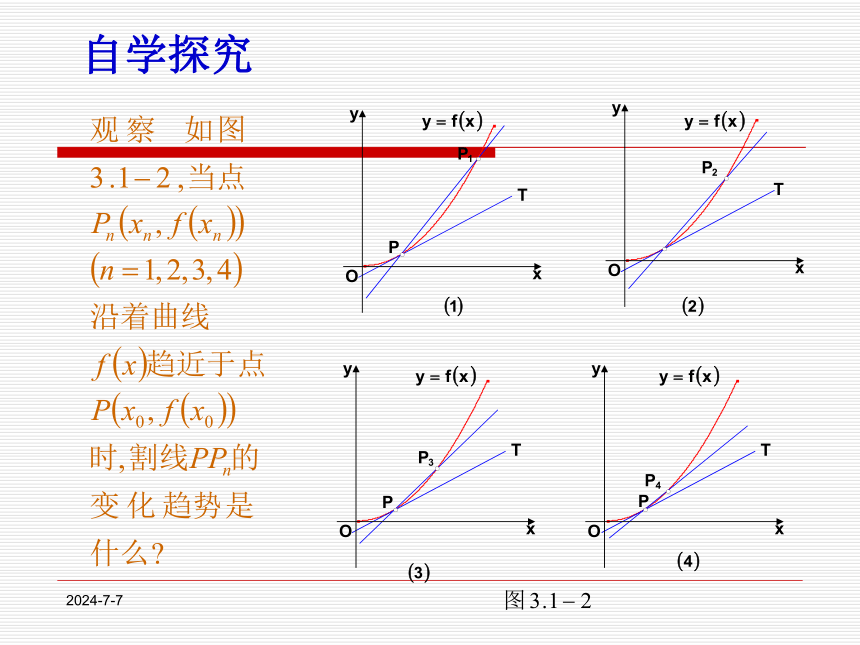
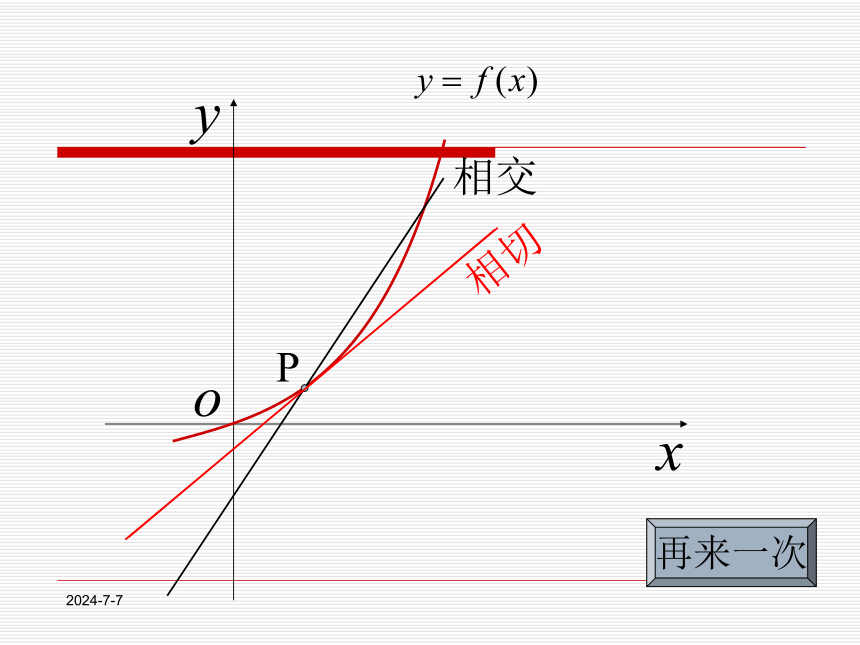
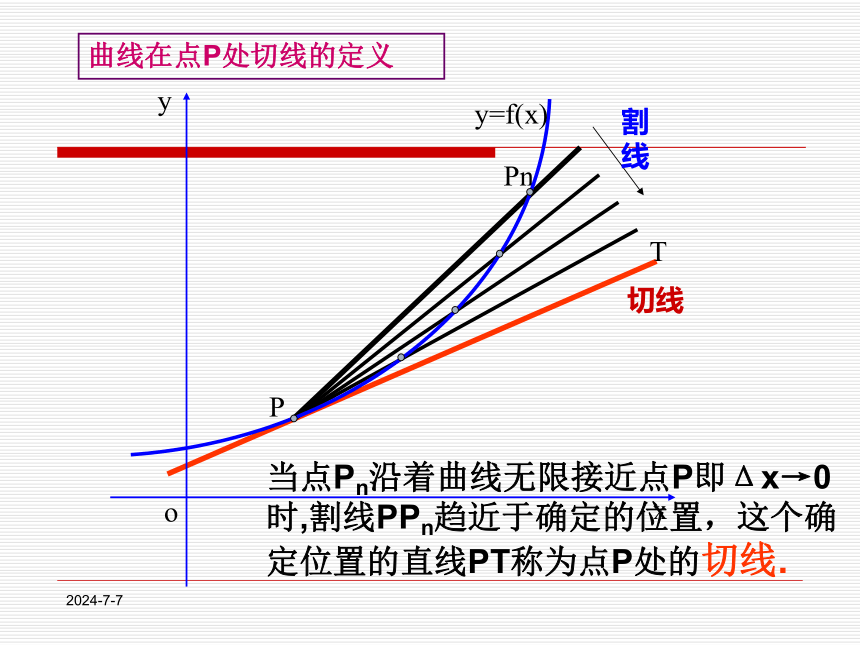
课件18张PPT。1.1.3导数的几何意义2019-12-301、平均变化率 一般地,函数 在区间上 的平均变化率为 割线的斜率f(x2)-f(x1)=△y复习引入2019-12-302.导数的概念3.求函数在 处的导数的步骤(1)求平均变化率(2)取极限y=f(x)在x=x0 处的导数2019-12-30提出问题2019-12-30自学探究2019-12-30P相切相交再来一次2019-12-30PPn切线T当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.曲线在点P处切线的定义2019-12-30M△x△y割线的斜率与切线的斜率有什么关系呢? 即:当△x→0时,割线PQ的斜率的极限,就是曲线在点P处的切线的斜率,小组交流2019-12-30因此,切线方程为y-2=2(x-1),
即y=2x.2019-12-30求切线方程的一般步骤:2019-12-302019-12-302019-12-302019-12-302019-12-30hto变式2019-12-30 结论:根据导数的几何意义,
当某点处导数大于零时,说明在这点的附近曲线是上升的,即函数在这点附近是单调递增;
当某点处导数小于零时,说明在这点的附近曲线是下降的,即函数在这点附近是单调递减;
2019-12-303、求切线方程的步骤:总结1、导数的几何意义:2、切线的斜率:2019-12-30课后作业1、习题3.1 A组 第5、6题。2019-12-30
即y=2x.2019-12-30求切线方程的一般步骤:2019-12-302019-12-302019-12-302019-12-302019-12-30hto变式2019-12-30 结论:根据导数的几何意义,
当某点处导数大于零时,说明在这点的附近曲线是上升的,即函数在这点附近是单调递增;
当某点处导数小于零时,说明在这点的附近曲线是下降的,即函数在这点附近是单调递减;
2019-12-303、求切线方程的步骤:总结1、导数的几何意义:2、切线的斜率:2019-12-30课后作业1、习题3.1 A组 第5、6题。2019-12-30
